25/26 材料合成S1期末复习题Week8

---

Question 8.1

---

核心理论基础：Ehrenfest Classification

在热力学中，我们根据吉布斯自由能（Gibbs Free Energy，用字母 G 表示）的导数行为来对相变进行分类。

对于任何热力学系统，吉布斯自由能 G 的全微分（Total Differential）定义如下：

$$
dG = VdP – SdT
$$

在这个公式中，字母含义如下：

• G：吉布斯自由能 (Gibbs Free Energy)
• P：压强 (Pressure)
• V：体积 (Volume)
• T：温度 (Temperature)
• S：熵 (Entropy)

根据微积分的知识，我们可以得到 G 关于 T 和 P 的一阶导数（First Order Derivatives）：

1. 对温度的导数（对应熵 S）：

$$
\left(\frac{\partial G}{\partial T}\right)_P = -S
$$

2. 对压强的导数（对应体积 V）：

$$
\left(\frac{\partial G}{\partial P}\right)_T = V
$$

---

什么是“一级相变” (First Order Phase Transformation)?

根据埃伦费斯特（Ehrenfest）的定义，一级相变是指：在相变点（例如冰变成水的瞬间），吉布斯自由能 G 是连续的，但是 G 的一阶导数（First Derivatives）是不连续的（Discontinuous）。

也就是说，在一级相变发生时，系统的熵（Entropy, S）和体积（Volume, V）会发生突变。

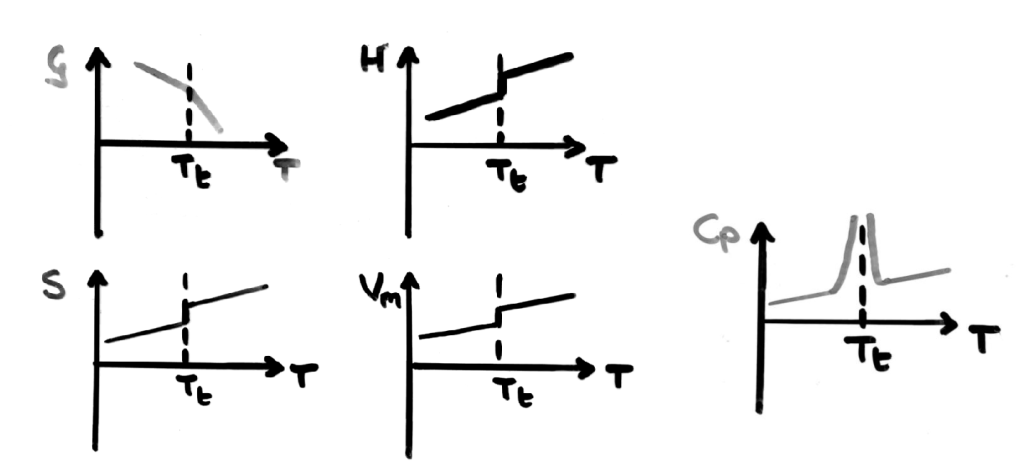
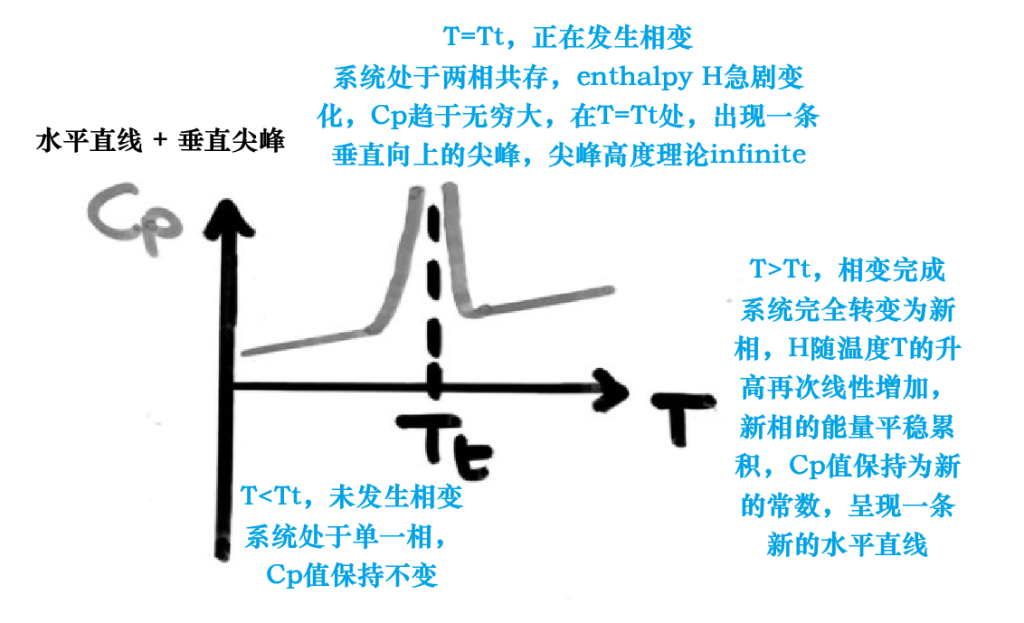
定压比热容 Cp 是焓 H 对温度 T 的 First-Order Partial Derivative ；物理上，正因为 First Order Phase Transformation 中焓 H 不连续（Discontinuous），导致 Cp 也不连续，表现为相变温度处的垂直尖峰（Infinite Peak）.

让我们根据这个定义来逐个分析选项.

---

选项详细解析

选项 (A) $\Delta S_m \neq 0$

这里的 m 下标代表摩尔（Molar）量，即每摩尔物质的量。$\Delta$ 代表变化量（终态减去初态）。

根据上面的推导，熵 S 是 G 的一阶导数。因为是一级相变，一阶导数必须是不连续的，这意味着 S 在相变前后会发生突变，不相等。

$$
S_{final} \neq S_{initial}
$$

因此：

$$
\Delta S_m = S_{final} – S_{initial} \neq 0
$$

结论： 选项 (A) 是正确的。这是由一级相变的定义直接得出的。这也意味着一级相变伴随着潜热（Latent Heat）的吸收或释放（因为热量 $Q = T\Delta S$）。

选项 (B) $\Delta V_m \neq 0$

同样的逻辑，体积 V 是 G 关于压强 P 的一阶导数。在一级相变中，一阶导数不连续，意味着体积 V 会发生突变。

例如，水结成冰时，体积会瞬间膨胀。这就是体积的突变。

$$
V_{final} \neq V_{initial}
$$

因此：

$$
\Delta V_m \neq 0
$$

结论： 选项 (B) 也是正确的。这代表相变过程中物质的密度（Density）发生了改变。

选项 (C) $\Delta H_m = 0$

这里的 H 代表焓（Enthalpy）。我们需要用到吉布斯自由能的定义公式：

$$
G = H – TS
$$

在恒温相变点（Equilibrium Temperature），两相的吉布斯自由能是相等的（$\Delta G = 0$）。所以我们可以写出变化量的关系：

$$
\Delta G = \Delta H – T\Delta S = 0
$$

移项得到：

$$
\Delta H = T\Delta S
$$

我们在分析选项 (A) 时已经确定了 $\Delta S \neq 0$。既然 $T$（绝对温度）不为零，且 $\Delta S$ 不为零，那么：

$$
\Delta H \neq 0
$$

这在物理上意味着相变必须吸收或释放热量，也就是存在潜热（Latent Heat）。如果 $\Delta H = 0$，那就没有潜热了，这不符合一级相变（如沸腾、融化）的特征。

结论： 选项 (C) 是错误的。

选项 (D) $c_p$ is continuous through the transformation

这里 $c_p$ 指的是恒压热容（Heat Capacity at Constant Pressure）。

热容是熵关于温度的导数，也就是 G 的二阶导数（Second Order Derivative）：

$$
c_p = T \left(\frac{\partial S}{\partial T}\right)_P = -T \left(\frac{\partial^2 G}{\partial T^2}\right)_P
$$

在一级相变中，熵 S 自身已经发生了突变（像一个台阶一样的跳跃）。

在数学上，如果一个函数（这里是 S）在某一点是不连续的（跳跃），那么它在该点的导数（这里对应 $c_p$）趋向于无穷大（Infinity）。

想象一下，在沸点，你不断加热（提供能量，即焓 H 增加），但在水全部变成蒸汽之前，温度 T 保持不变。这意味着你输入了热量但温差 $dT$ 为 0。

$$
c_p = \frac{dH}{dT} \rightarrow \infty
$$

所以，$c_p$ 在一级相变点不仅不是连续的，甚至可以说是奇异的（Singular/Infinite）。

结论： 选项 (D) 是错误的。

---

最终答案总结

这道题是一道多选题（Multiple Select Question）。符合一级相变特征的选项是：

A 和 B

• (A) $\Delta S_m \neq 0$：正确。熵发生突变，意味着有潜热。
• (B) $\Delta V_m \neq 0$：正确。体积发生突变，意味着密度改变。

(注意：考试中如果必须单选，通常会根据特定教材的侧重点选择，但在严格的热力学定义中，A和B都是一级相变的定义性特征。鉴于这是“Characteristic features”（复数），A和B都应入选。)

加油！这部分概念很抽象，只要记住“一级相变 = 一阶导数(S和V)突变”这个口诀，就能解决大部分问题。

Question 8.3

题干解析

原文：
“The driving force for a transformation may be expressed in terms of supercooling or supersaturation. In which of the following transformation is it conventional to use supercooling?”

中文详解：
相变（Transformation）的驱动力（Driving Force）可以用过冷度（Supercooling）或者过饱和度（Supersaturation）来表示。在下列哪种相变中，习惯上（Conventional）使用过冷度（Supercooling）？

这里的核心在于区分两个概念：

1. 过冷度（Supercooling）：主要与温度差有关。
2. 过饱和度（Supersaturation）：主要与浓度或压强有关。

为了拿满分，我们需要从热力学公式推导来理解为什么会有这种区分。

---

核心理论：相变驱动力 (Driving Force for Phase Transformation)

在热力学中，相变发生的根本原因是因为新相的吉布斯自由能（Gibbs Free Energy）比旧相更低。这个能量差就是驱动力。

我们用 $\Delta G$ 表示吉布斯自由能变化（Gibbs Free Energy Change）。

当系统处于平衡温度（Equilibrium Temperature，记为 Tm）时，两相能量相等，$\Delta G$ 为零。
当偏离平衡状态时，驱动力可以用以下近似公式表示（对于小范围偏离）：

$$
\Delta G \approx \frac{L \cdot \Delta T}{T_m}
$$

在这个公式中：

• L：潜热（Latent Heat）
• Tm：熔点或平衡温度（Melting Point / Equilibrium Temperature）
• $\Delta T$：过冷度（Undercooling / Supercooling）

公式告诉我们：如果我们通过降低温度（Lowering Temperature）来驱动相变，驱动力的大小直接正比于温差 $\Delta T$。这就是过冷的概念。

过冷度（supercooling, ΔT）是宏观可直接测量的间接量化指标，而相变的本质驱动力是过冷度引发的吉布斯自由能差（change in Gibbs free energy, ΔG）—— 只有当 ΔG<0 时，相变才会自发进行

另一方面，如果相变是由于溶质浓度（Concentration）过高引起的，驱动力通常写成：

$$
\Delta G = -RT \ln \left( \frac{C}{C_{eq}} \right)
$$

在这里：

• C：当前的浓度（Concentration）
• Ceq：平衡时的溶解度（Equilibrium Solubility）
• 比值 $C/C_{eq}$：这就是过饱和度（Supersaturation）

常规表达式（直接关联溶质浓度差）

$$\Delta \mu = k T \ln \frac{X}{X_e}$$

• Δμ：Change in Chemical Potential
• k：Boltzmann Constant，1.38×10⁻²³ J・K⁻¹
• T：Absolute Temperature
• X：Actual Solute Concentration, X>Xₑ
• Xₑ：Equilibrium Solute Concentration，对应温度 T 下的饱和浓度

数学逻辑：当溶质浓度过高（X>Xₑ，过饱和状态），ln (X/Xₑ)>0，若 Δμ<0（需结合相变类型判断符号，溶液结晶时 Δμ 为负），相变自发进行；

物理意义：浓度差（X – Xₑ）越大，ln (X/Xₑ) 的值越大，驱动力 Δμ 的绝对值越大，结晶相变越容易发生（比如盐水蒸发后食盐结晶，就是因为水分减少导致 X 升高，超过 Xₑ后自发结晶）

替代表达式（关联过冷度，间接反映浓度影响）

$$\Delta \mu = \frac{\Delta H_m^{sol} \cdot \Delta T}{T_{sol}}$$

• ΔHₘ^sol：Enthalpy of Solution，单位 J・mol⁻¹，结晶是溶解的逆过程，符号相反
• ΔT：Undercooling，ΔT=Tₛₒₗ – T，Tₛₒₗ是饱和温度，浓度越高 Tₛₒₗ越低
• Tₛₒₗ：Saturation Temperature，单位 K，对应浓度 Xₑ的相变温度

物理意义：溶质浓度过高会降低饱和温度 Tₛₒₗ，使实际温度 T 与 Tₛₒₗ的差值 ΔT 增大，进而增大驱动力 Δμ—— 本质是 “浓度过高” 通过改变平衡温度间接提供驱动力.

总结：

• 凡是主要靠降温导致纯物质状态改变的，习惯用过冷度（Supercooling）。
• 凡是主要靠溶质析出或气体冷凝（涉及组分浓度或分压变化）的，习惯用过饱和度（Supersaturation）。

---

选项详细解析

我们要找的是习惯用过冷度（Supercooling）的情况。

选项 (A) precipitation in the solid state

中文意思： 固态中的析出（沉淀）。
分析：
这是指一种金属固体中析出另一种微小的固体颗粒（例如铝合金的时效强化）。虽然这个过程通常也是通过降温引发的（因为低温下溶解度降低），但在描述其成核速率（Nucleation Rate）和生长（Growth）时，学术界习惯关注的是溶质原子在基体中的浓度（Concentration）超过了平衡溶解度。
因此，这里的核心变量是浓度的比值。

结论： 习惯使用 过饱和度（Supersaturation）。

选项 (B) condensation of a vapour

中文意思： 蒸汽的冷凝（气态变为液态）。
分析：
比如水蒸气变成雨滴。这个过程取决于蒸汽的分压（Partial Pressure）是否超过了该温度下的饱和蒸汽压（Saturation Vapor Pressure）
虽然降温可以导致冷凝，但在热力学描述中，驱动力通常被定义为压强的比值（类似于浓度的比值）

$$
S = \frac{P}{P_{eq}}
$$

结论： 习惯使用 过饱和度（Supersaturation）

选项 (C) boiling of a liquid

中文意思： 液体的沸腾（液态变为气态）。
分析：
沸腾发生的条件是温度高于沸点。这叫过热（Superheating），而不是过冷（Supercooling）。方向反了。

结论： 这是一个干扰项，不符合题目语境。

选项 (D) crystallisation of a melt

中文意思： 熔体的结晶。
分析：
Melt 这个词在材料科学中通常指纯物质的熔融液（例如融化的纯金、纯铜，或者液态水结冰）。
对于纯物质的凝固，没有“浓度”的变化（因为它只有一种成分）。唯一的变量就是温度（Temperature）。
液态金属要变成固态晶体，液体的温度必须低于熔点 Tm。这个温差 $Tm – T$ 就是唯一的驱动力衡量标准。

$$
\Delta T = T_m – T
$$

这就是最典型的过冷（Supercooling）应用场景

结论： 习惯使用 过冷度（Supercooling）

---

最终答案

正确答案是 (D)

解题思路总结：
看到 Melt（熔体）这个词，就要立刻反应过来这是纯液体的凝固（Solidification of pure liquid）；对于纯液体的凝固，温度差是唯一的驱动力来源，因此学术界定义这种驱动力为过冷度（Supercooling）

Question 8.4

这道题其实非常基础，考察的是表面能（Surface Energy）对物体形状的影响，只要你弄懂了“液体”和“晶体”在微观结构上的区别，这道题就是送分题.

---

核心理论：为什么物体会有特定的形状？

在热力学中，所有的物体在平衡状态（Equilibrium State）下，都试图让系统的总能量降到最低。对于微小的液滴或晶体，决定形状的关键能量是界面自由能（Interfacial Free Energy）.

系统总的界面能 G 可以用下面的公式表示：

$$
G = \int \gamma dA
$$

在这个公式中：

• G：吉布斯自由能（Gibbs Free Energy）。
• $\gamma$：界面能（Interfacial Energy）或者表面张力（Surface Tension）。
• A：界面面积（Interfacial Area）。

为了让 G 最小，物体会调整自己的形状。这里只有两种情况：

情况 1：各向同性（Isotropy）—— 形成球体

如果物质内部原子排列没有规则（比如液体、气体、非晶体），那么无论你从哪个方向看，它的性质都是一样的。
这意味着 $\gamma$ 是一个常数，不随方向改变。

$$
\gamma(\theta, \phi) = \text{constant}
$$

在这种情况下，要让总能量 G 最小，只需要让表面积 A 最小。
在体积固定的情况下，球体（Sphere）拥有最小的表面积。

情况 2：各向异性（Anisotropy）—— 形成多面体

如果物质是晶体（Crystal），原子是整齐排列的。不同的晶面（比如立方体的面和棱）原子密度不同，断键数量也不同。
这意味着 $\gamma$ 随方向改变，这叫做各向异性（Anisotropy）。

$$
\gamma(\theta, \phi) \neq \text{constant}
$$

在这种情况下，晶体会尽量暴露那些 $\gamma$ 值最小的面。最终形成的形状是有棱角的多面体（Faceted Polyhedron），而不是圆滑的球体。

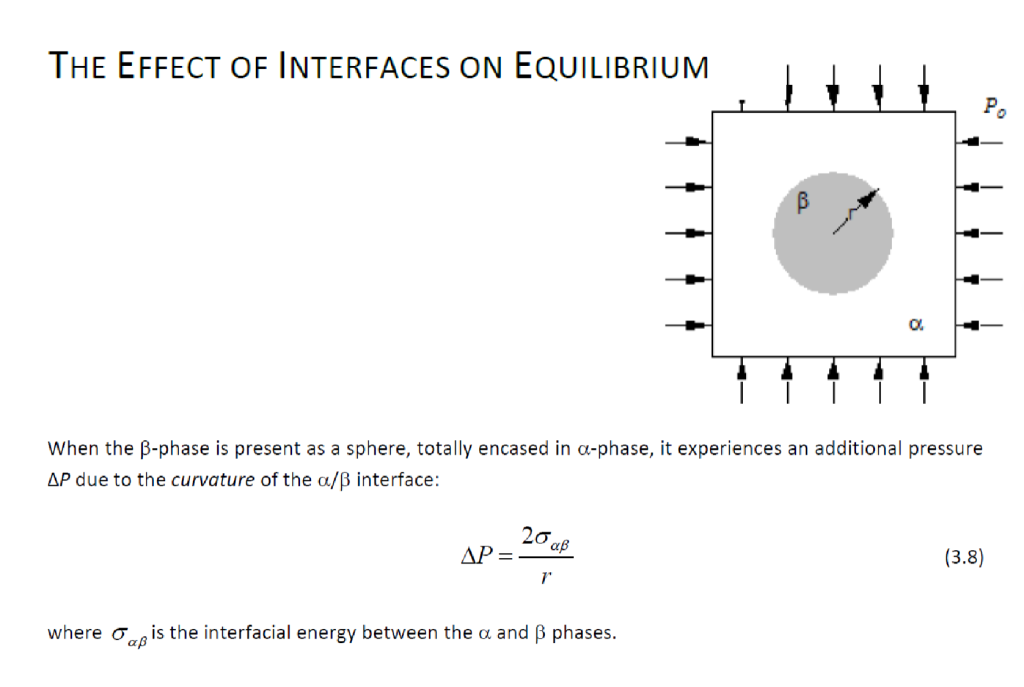
球体相的附加压力公式

$$\Delta P = \frac{2\sigma_{\alpha\beta}}{r}$$

• 学术名词标注：
  • ΔP：附加压力（Additional Pressure）；
  • $\sigma_{\alpha\beta}$：α 相（橄榄油）与 β 相（空气）的界面能（Interfacial Energy）；
  • r：球体半径（Sphere Radius）
• 公式意义：该公式证明球体是流体分散相的稳定形态，进一步支撑 “气泡形成球体” 的结论

---

选项详细解析

我们利用上面的理论来排查选项。

选项 (A) air bubbles in olive oil

中文翻译：橄榄油中的气泡。

• 物质分析：空气是气体，橄榄油是液体。它们内部都没有规则的原子排列结构。
• 性质判定：它们的界面能是各向同性（Isotropic）的。
• 结果：为了表面积最小化，气泡会变成球体（Sphere）。
• 结论：符合。

选项 (B) ice crystals in air

中文翻译：空气中的冰晶。

• 物质分析：注意题目中的词 Crystals（晶体）。冰是晶体固体，有固定的晶格结构。
• 性质判定：冰的界面能是各向异性（Anisotropic）的。即 $\gamma$ 随晶体取向变化（这在教材中通常称为 $\gamma$-plot）。
• 结果：冰晶会形成雪花状、六棱柱状等有棱角的形状，这种现象叫做小面化（Faceting）。
• 结论：不符合。

选项 (C) water droplets in air

中文翻译：空气中的水滴。

• 物质分析：水是液体，空气是气体。流体分子是混乱运动的。
• 性质判定：界面能是完全各向同性（Isotropic）的。
• 结果：表面张力会把水滴拉紧，形成表面积最小的形状，即球体（Sphere）。（就像雨滴或露珠）。
• 结论：符合。

选项 (D) quartz crystals in silica glass

中文翻译：石英玻璃中的石英晶体。

• 物质分析：虽然外面的玻璃是非晶体，但里面的主角是 Quartz Crystals（石英晶体）。只要是晶体，原子就有序排列。
• 性质判定：晶体的界面能是各向异性（Anisotropic）的。
• 结果：石英晶体会长成有棱角的多面体形状，以配合其最低能量的晶面。
• 结论：不符合。

---

最终答案

这是一道多选题（Multiple Choice），符合条件的选项是：

A 和 C

---

总结记忆法：

• 看到 Liquid（液体）、Gas（气体）、Bubble（气泡）、Droplet（液滴） $\rightarrow$ 选 Sphere（球体）。
• 看到 Crystal（晶体）、Solid（固体）、Metal（金属） $\rightarrow$ 非球体（Non-spherical / Faceted）。

Question 8.5

题目答案

10μm汽油液滴（liquid droplet of gasoline）的沸点（Boiling Point）高于块状汽油（bulk sample of gasoline）的沸点

逻辑：液滴的弯曲界面（curved interface）产生附加压力（Additional Pressure），使液滴内部蒸气压（Vapour Pressure）升高，需更高温度才能让蒸气压等于外界压力，达到沸点条件

弯曲界面与附加压力

$$\Delta P = \frac{2\sigma_{\alpha\beta}}{r}$$

• ΔP：附加压力（Additional Pressure，单位Pa）；
• $\sigma_{\alpha\beta}$：液-气界面能（Liquid-Vapour Interfacial Energy，文档中常用σLV表示，单位J·m⁻²，是两相间过渡区的键合破坏能）
• r：液滴的曲率半径（Radius of Curvature，单位m，液滴为凸面，r取正值；块状物质界面可视为平面，r→∞）

---

• 物理意义

液体内部原子被周围原子包围，受力平衡；液滴表面的原子仅一侧有相邻原子，受力不平衡，产生表面张力（Surface Tension）；表面张力会使液滴产生“收缩”趋势，导致液滴内部压力高于外部环境压力，这部分额外压力就是附加压力ΔP

• 关键规律：r越小，ΔP越大（10μm液滴的r=10⁻⁵m，远小于块状物质的r→∞，因此液滴的ΔP远大于0，块状物质的ΔP≈0）

附加压力对蒸气压的影响

CAPE2710 Week4 (2025) 中明确说明 “the vapour pressure in equilibrium with a liquid droplet increases with decreasing droplet radius”（与液滴平衡的蒸气压随液滴半径减小而增大）

• 物理原因

液滴内部的附加压力ΔP会“挤压”原子，使原子更易脱离液面形成蒸气（蒸气压本质是原子脱离液相的倾向）。因此：

1. 块状汽油（r→∞，ΔP≈0）：蒸气压为正常蒸气压P块
2. 10μm液滴（r=10⁻⁵m，ΔP>0）：蒸气压P滴 = P块 + ΔP > P块

蒸气压与沸点的关联

• 沸点的定义
  沸点是“液体蒸气压等于外界环境压力（如大气压）时的温度”——当液体蒸气压与外界压力相等时，液体内部会持续产生气泡，发生沸腾
• 沸点差异的推导

块状汽油：要沸腾，需温度升高到T块，使P块 = 外界压力

10μm液滴：因P滴 > P块，需升高到更高温度T滴，才能使P滴 = 外界压力

结论：T滴 > T块，即液滴沸点高于块状汽油

文档中类似案例验证

CAPE2710 Week4 (2025).pdf（文档2），Week4 Task1b“Melting temperature”部分提到：

• 微小固体颗粒的熔点（Melting Point）低于块状固体，本质是弯曲界面的附加压力影响相变平衡温度；
• 规律延伸：弯曲界面对相变温度的影响具有一致性——凸面（液滴、固体颗粒）会使“吸热相变”（如液→气、固→液）的温度向“更高”方向偏移（液滴沸点升高），向“放热相变”的温度向“更低”方向偏移（固体颗粒熔点降低）

选项分析（逐一排除+依据）

• 选项A：the same as that of a bulk sample of gasoline（与块状样品相同）
• 错误原因：块状样品的界面为平面（r→∞），附加压力ΔP≈0，蒸气压为正常数值；液滴界面为弯曲面（r极小），ΔP>0，蒸气压更高，需不同温度才能达到沸点，因此沸点不同。
• 选项B：higher than that of a bulk sample of gasoline（高于块状样品）

正确原因：如上述推导，液滴附加压力导致蒸气压升高，需更高温度使蒸气压等于外界压力，沸点更高，完全符合文档中“蒸气压随半径减小而增大”的结论。

• 选项C：lower than that of a bulk sample of gasoline（低于块状样品）

错误原因：混淆了“液滴”与“固体颗粒”的相变温度规律——固体颗粒因凸面附加压力，熔点降低，但液滴的液→气相变是吸热过程，凸面附加压力导致沸点升高，二者规律相反

疑难：为什么不用Clausius-clapeyron equation判断沸点差异

Clausius-Clapeyron Equation 不能用于判断10μm液滴与块状汽油的沸点差异，因为它默认“平面界面”（无附加压力），未考虑液滴弯曲界面产生的 Additional Pressure 对蒸气压的影响

Molar Enthalpy 相同仅说明物质本身的相变能量相同，但界面曲率会改变蒸气压，进而改变沸点，因此两者沸点不同.

$$\left(\frac{dP}{dT}\right){eqm} = \frac{\Delta H{m}^{\alpha \to \beta}}{T \cdot \Delta V_{m}^{\alpha \to \beta}}$$

• dP/dT：Rate of Vapour Pressure Change with Temperature
• ΔHm^α→β：相变摩尔焓Molar Enthalpy of Phase Transformation，单位J·mol⁻¹，是物质固有属性
• T：Phase Transformation Temperature，此处为沸点，单位K
• $\Delta V_m^{\alpha→\beta}$：Molar Volume Change of Phase Transformation，单位m³·mol⁻¹

Clausius-Clapeyron Equation描述平面界面下，蒸气压与相变温度（如沸点、熔点）的关系

例如：计算不同外界压力下，块状物质（平面界面）的沸点变化（如高山上气压低，水的沸点低于100℃）

• 适用条件

1. 界面为平面：默认两相界面无曲率（r→∞），因此无附加压力（ΔP=0）
2. 相变过程中，摩尔焓（ΔHm）和摩尔体积变化（ΔVm）为常数（与物质本身相关，块状和液滴的ΔHm确实相同）；- 仅考虑外界压力对蒸气压的影响，不考虑界面曲率导致的“内禀蒸气压变化”

液滴是“凸面界面”（Curved Convex Interface），根据附加压力公式：

$$\Delta P = \frac{2\sigma_{LV}}{r}$$

• 物理意义：液滴半径r越小，附加压力ΔP越大（10μm液滴的r=10⁻⁵m，ΔP远大于0），导致液滴内部蒸气压（P滴）= 块状物质蒸气压（P块）+ ΔP，即P滴 > P块

计算相变的吉布斯自由能，先通过 Clausius-clapeyron equation 计算 “平面界面”（无附加压力）下的相变温度（如沸点、熔点），再通过 Additional pressure 的 “修正效应” 调整 “弯曲界面”（如液滴、小颗粒）的实际相变温度；平面界面时，附加压力 ΔP=0，修正项为 0，相变温度就是克劳修斯 – 克拉佩龙方程的计算结果；弯曲界面时，需用附加压力修正，实际相变温度偏离基础值.

沸点的本质是“蒸气压=外界压力”的温度，而蒸气压不仅受摩尔焓影响，还受界面曲率（附加压力） 影响——液滴的弯曲界面改变了蒸气压，因此即使摩尔焓相同，沸点也不同.

Question 8.6

考察内容：小角度晶界的位错阵列组成

Low Angle Tilt Boundary由刃型位错（Edge Dislocations） 阵列形成；小角度扭转晶界（Low Angle Twist Boundary）由螺型位错（Screw Dislocations） 阵列形成

这是小角度晶界（Low Angle Grain Boundaries）的两种基本类型，其结构本质是通过特定位错的规则排列，来协调相邻晶粒的小角度取向差（通常<10°-15°）

小角度倾斜晶界：刃型位错阵列

定义

• 小角度倾斜晶界（Low Angle Tilt Boundary）：相邻晶粒绕垂直于晶界平面的轴发生小角度旋转（Misorientation Angle θ<10°-15°），晶界平面平行于旋转轴，形成的晶界类型。
• 刃型位错（Edge Dislocation）：位错线与滑移方向垂直，原子排列呈现 Extra Half-Plane 的特征，只能在 Slip Plane 上滑动，主要产生晶粒的倾斜变形.

位错阵列的作用原理

• 相邻晶粒存在小角度取向差时，原子排列的错配无法通过连续过渡协调，需通过刃型位错的规则排列来“补偿”错配；
• 刃型位错的“额外半原子面”沿晶界方向均匀分布，位错线相互平行，且垂直于晶粒的旋转轴；
• 位错之间的间距与取向差θ成反比，取向差越小，位错间距越大，晶界能量越低（符合文档中“小角度晶界能量随取向差增大而升高”的规律）。

小角度扭转晶界：螺型位错阵列

定义

• 小角度扭转晶界（Low Angle Twist Boundary）：相邻晶粒绕平行于晶界平面的轴发生小角度旋转（取向差θ<10°-15°），晶界平面垂直于旋转轴，形成的晶界类型
• 螺型位错（Screw Dislocation）：位错线与滑移方向平行，呈 Helical Atomic Arrangement，可沿滑移面滑动或攀移，主要产生晶粒的扭转变形

位错阵列的作用原理

• 晶粒绕平行于晶界的轴旋转时，原子排列的错配需通过两组相互垂直的螺型位错阵列来协调
• 螺型位错的螺旋状原子排列可抵消旋转带来的晶格扭转，两组位错交叉形成“网格状”阵列，覆盖整个晶界平面
• 与倾斜晶界类似，扭转晶界的位错密度也与取向差θ成正比，θ越小，位错密度越低，晶界越稳定

总结

关键文档内容

1. 螺型位错（Screw Dislocation）的定义与图示（CAPE1720 L15-18），明确其“位错线与滑移方向平行”的特征，与扭转晶界的扭转协调需求一致；
2. 小角度晶界的能量规律（图3.9）同样适用于扭转晶界，证明其位错阵列的低能量结构；
3. 文档中“位错运动方向”的描述（Edge Dislocation与Screw Dislocation的运动差异），支撑两种位错分别适配倾斜和扭转变形的逻辑。

小角度晶界的核心特征

取向差θ<10°-15°（文档图3.9明确阈值）

由位错规则阵列组成，能量远低于大角度晶界

分为倾斜（绕垂直晶界轴旋转）和扭转（绕平行晶界轴旋转）两类，分别对应不同位错类型

---

Question 8.7

核心结论

题目空白处答案：第一空填 self-（对应自扩散），第二空填 polymer（对应聚合物）

完整句子：“In polymers, self- diffusion can be largely ignored, due to strong intermolecular bonds and the length and entanglement of polymer chains, but the diffusion of foreign molecules through the regions between polymer molecular chains (particularly amorphous ones) can be significant particularly in thin films.”

self- diffusion

术语定义与英文标注

Self-Diffusion：指同一种 polymer molecules 之间的扩散，即聚合物自身的分子在分子链网络中移动的现象

关键内容

文档出处：CAPE2710 Week4 Task3（文档1），e-book pages97-114“Diffusion”部分；CAPE2710 Week7 Task3（文档4），e-book pages176-183“Polymer Crystallisation”部分

1. Week4 Task3明确“ Self-Diffusion 是同种物质原子/分子的扩散”，且“ Diffusion Coefficient 远低于金属/陶瓷”
2. Week7 Task3提到“ Polymer Chains 长且 Entanglement，分子间作用力强，导致分子移动困难”

为什么自扩散可忽略？（题目核心原因）

• 分子链长且缠结：聚合物分子是长链结构，链与链之间相互缠绕，像“乱麻”一样，阻碍自身分子移动
• 分子间作用力强：聚合物分子间存在范德华力（Van der Waals Forces）等强相互作用，进一步限制分子自由扩散
• 文档结论：Week4 Task3明确“聚合物的自扩散系数（Self-Diffusion Coefficient）极小，在实际应用中可忽略”与题目描述完全一致

polymer molecular chains

术语定义与英文标注

• 聚合物分子链（Polymer Molecular Chains）：聚合物的基本结构单元，由重复的单体（Monomer）通过化学键连接形成的长链；
• 外来分子（Foreign Molecules）：指聚合物之外的小分子物质（如气体、溶剂分子等）；
• 无定形区域（Amorphous Regions）：聚合物中分子链无规则排列的区域（对应结晶区域Crystalline Regions），是外来分子扩散的主要通道。
• 英文学术名词：聚合物分子链（Polymer Molecular Chains）、外来分子（Foreign Molecules）、无定形区域（Amorphous Regions）、结晶区域（Crystalline Regions）。

关键内容

文档出处：CAPE2710 Week7 Task3（文档4），e-book pages176-183“Polymer Crystallisation”部分；CAPE2710 Week4 Task3（文档1），e-book pages97-114“Diffusion in Polymers”部分

1. Week7 Task3描述“聚合物包含结晶区域（分子链规则排列）和无定形区域（分子链无规则排列），无定形区域的分子链间隙（Regions Between Chains）为外来分子提供扩散通道”
2. Week4 Task3提到“小分子体积小，能快速通过聚合物的无定形区域间隙扩散，Thin Polymer Films 中这种扩散更显著”，与老师提示“Small molecules can diffuse rapidly through many thin polymer films”完全呼应

为什么外来分子扩散显著？（题目核心原因）

• 分子链间隙存在：聚合物分子链之间存在天然的“空隙”，尤其是无定形区域，空隙更大，为外来小分子提供了扩散路径
• 小分子体积小：外来分子（如O₂、CO₂等）体积远小于聚合物分子链，能轻松穿过分子链间隙
• 薄膜的特殊性：薄聚合物膜的厚度小，外来分子需要扩散的距离短，进一步增强扩散的显著性

外来小分子 → 穿过 Thin Polymer Films → Rapid Diffusion ；聚合物 Self-Diffusion → 可忽略

Week4 Task3明确“聚合物中，外来小分子的扩散（Impurity Diffusion/Interdiffusion）显著，而自扩散可忽略”，这是聚合物扩散的核心特征，也是考试必考点

Question 8.9

核心结论

答案为 True（正确）

金（Gold）能在硅（Silicon）中形成间隙固溶体（Interstitial Solid Solution），且因间隙扩散（Interstitial Diffusion）机制，在硅的晶格（Lattice）中扩散相对较快——核心原因是硅的晶体结构为低堆积密度的金刚石立方结构，能容纳金原子进入间隙位置，且间隙扩散无需依赖空位，扩散阻力小、速度快

Interstitial Solid Solution

• 学术定义：溶质原子（Solute Atom，此处为金原子）嵌入溶剂原子（Solvent Atom，此处为硅原子）晶体结构的间隙位置（Interstitial Sites）形成的固溶体，溶质原子尺寸通常小于溶剂原子的间隙尺寸
• 英文学术名词：间隙固溶体（Interstitial Solid Solution）、溶质原子（Solute Atom）、溶剂原子（Solvent Atom）、间隙位置（Interstitial Sites）
• 文档依据：CAPE2710 Week4 Task3（文档1），e-book pages97-114“Diffusion”部分；Week2 Task3（文档8）e-book pages25-35“Thermodynamics of Alloy Systems”中“间隙固溶体（Interstitial Solution）”的定义（Porter & Easterling图示说明）

硅的晶体结构：Diamond Cubic Structure

• 核心特征：硅的晶体结构为金刚石立方结构，原子排列疏松，堆积密度（Packing Density）仅约34%（远低于密排结构的74%），存在大量未被原子占据的间隙位置（如四面体间隙、八面体间隙），为金原子提供容纳空间
• 英文学术名词：金刚石立方结构（Diamond Cubic Structure）、堆积密度（Packing Density）、四面体间隙（Tetrahedral Interstitial Sites）、八面体间隙（Octahedral Interstitial Sites）
• 文档依据：CAPE2710 Week4 Task1a（文档1），e-book pages74-89“THE SOLID-LIQUID INTERFACE”部分提到半导体（Si、Ge）的晶体结构特征；Week2 Task3（文档8）中“间隙固溶体形成条件”明确“溶剂晶体结构堆积密度低时，易形成间隙固溶体”

金的扩散机制：Interstitial Diffusion

• 扩散原理：金原子作为溶质，嵌入硅的间隙位置后，扩散时无需像置换固溶体（Substitutional Solid Solution）那样依赖空位（Vacancy），仅需克服相邻间隙间的能量壁垒，扩散激活能（Activation Energy for Diffusion）低，因此扩散速度相对较快
• 英文学术名词：间隙扩散（Interstitial Diffusion）、置换固溶体（Substitutional Solid Solution）、空位（Vacancy）、扩散激活能（Activation Energy for Diffusion）、晶格扩散（Lattice Diffusion）。
• 文档依据：CAPE2710 Week4 Task3（文档1）e-book pages97-114“Diffusion”部分明确“间隙扩散是溶质原子在溶剂间隙中迁移，扩散系数（Diffusion Coefficient）高于置换扩散”；“间隙扩散无需空位，适用于溶质原子尺寸较小或溶剂堆积密度低的体系”

题目逻辑链

1. 金与硅的尺寸适配性：金原子（原子半径约0.144 nm）虽大于硅原子（原子半径约0.117 nm），但硅的金刚石立方结构间隙尺寸（如四面体间隙半径约0.031 nm）虽小，但其堆积密度极低，间隙区域的“有效空间”足以容纳金原子（实际为金原子部分嵌入间隙，伴随轻微晶格畸变，但仍属于间隙固溶体）——这与题目反馈“Gold is a much large atom than silicon but the diamond cubic structure has a very low packing density so it is possible to incorporate large atoms into interstitial sites”完全一致。
2. 扩散速度的合理性：金在硅中通过间隙扩散，无需等待空位形成，扩散激活能低（远低于置换扩散的激活能），因此“diffuses relatively rapidly through the lattice”（相对快速扩散）成立——文档1 Week4 Task3明确“间隙扩散的扩散系数通常大于置换扩散，扩散速度更快”

易混淆点澄清（避免误解）

• 误区1：“大原子不能形成间隙固溶体”——错误；间隙固溶体的关键是“溶剂晶体间隙能否容纳溶质原子”，而非溶质原子绝对尺寸。硅的低堆积密度提供了足够空间，即使金原子较大，仍可嵌入间隙（伴随轻微晶格畸变，不影响固溶体类型）
• 误区2：“扩散快一定是置换扩散”——错误；扩散速度取决于扩散机制：间隙扩散无需空位，激活能低，扩散速度通常比置换扩散快，金在硅中的扩散正属于这种情况

总结：考试必记核心点

1. 间隙固溶体形成条件：溶剂晶体堆积密度低（如金刚石立方结构）+ 溶质原子可嵌入间隙
2. 金-硅体系：硅的低堆积密度→金形成间隙固溶体→间隙扩散→扩散较快
3. 英文关键词：Interstitial Solid Solution（间隙固溶体）、Diamond Cubic Structure（金刚石立方结构）、Interstitial Diffusion（间隙扩散）、Lattice（晶格）

考点	文档出处	关键内容
间隙固溶体定义	CAPE2710 Week2 Task3（文档8）e-book pages25-35	间隙固溶体的形成条件：溶剂堆积密度低、溶质原子尺寸适配间隙
硅的晶体结构	CAPE2710 Week4 Task1a（文档1）e-book pages74-89	半导体（Si、Ge）的晶体结构为金刚石立方，界面结构相关特征
间隙扩散特性	CAPE2710 Week4 Task3（文档1）e-book pages97-114	间隙扩散与置换扩散的区别、扩散速度对比
题目反馈依据	图片题目自带Feedback	金原子大但硅的堆积密度低，可容纳于间隙位置

Question 8.10

核心结论

Blank 1 答案：vacancy（对应空位扩散）；Blank 2 答案：interstitial（对应间隙扩散）

Vacancy Diffusion（空位扩散）

1. 术语定义与英文标注

• 空位扩散（Vacancy Diffusion）：晶体中原子（原子尺寸较大，如金属基体原子）通过与相邻的空位（vacant site）交换位置实现的扩散，是固体金属中最常见的扩散机制之一
• 关键英文学术名词：
• 空位扩散（Vacancy Diffusion）
• 正常晶格位置（Normal Lattice Position）
• 空位（Vacant Site）
• 晶格（Lattice）
• 扩散系数（Diffusion Coefficient, D）

2. 文档依据（精准定位）

• 文档出处：文档2（CAPE2710 Week4 Task3），e-book pages97-114“Diffusion”部分，小标题“In solid metals, two mechanisms of diffusion predominate”段落（page101）
• 关键文档内容：

“In solid metals, two mechanisms of diffusion predominate: a) Vacancy diffusion – Exchange between normal lattice position and adjacent vacant site; b) Interstitial diffusion – Migration from interstitial lattice site to adjacent vacant interstitial site.”

• 补充文档：文档2 Week4 Task3 e-book pages103“Diffusion Coefficients”部分，提到空位扩散的激活能（Activation Energy, Qd）与空位形成能相关.

3. 扩散机制详解（通俗解释）

1. 空位是晶体中的本征缺陷（热力学稳定存在），温度越高，空位浓度越高；
2. 原子要发生空位扩散，需要满足两个条件：

• 获得足够的热激活能（克服原子间结合力）；
• 相邻位置存在空位；

1. 过程：以金属Fe为例，Fe原子（占据正常晶格位置）获得能量后，移动到相邻的空位，原位置形成新的空位，后续原子继续填充，实现原子的宏观扩散。

4. 核心公式（空位扩散系数）

空位扩散系数遵循 Arrhenius relationship：
$$D = D_0 exp\left(-\frac{Q_d}{R T}\right)$$

• 符号含义：
• D₀：频率因子（与原子振动频率、晶格参数相关）
• Qd：扩散激活能（含空位形成能+原子迁移能）；
• R：气体常数（8.314 J/(mol·K)）
• T：热力学温度（K）

---

Interstitial Diffusion（间隙扩散）

1. 术语定义与英文标注

• 间隙扩散（Interstitial Diffusion）：溶质原子（尺寸较小，如C、N、H原子）嵌入溶剂晶体的间隙位置（interstitial lattice site）后，在相邻间隙位置之间迁移的扩散机制，无需依赖空位。
• 关键英文学术名词：
• 间隙扩散（Interstitial Diffusion）
• 间隙晶格位置（Interstitial Lattice Site）
• 溶质原子（Solute Atom）
• 溶剂晶体（Solvent Crystal）
• 空间隙位置（Vacant Interstitial Site）

2. 文档依据（精准定位）

• 文档出处：文档2（CAPE2710 Week4 Task3），e-book pages97-114“Diffusion”部分，小标题“In solid metals, two mechanisms of diffusion predominate”段落（page101）；文档8（2710 Week2 Task3） e-book pages25-35“Interstitial Solution”部分（图2.11c）。
• 关键文档内容：

“Interstitial diffusion – Migration from interstitial lattice site to adjacent vacant interstitial site. For large atomic size difference results in interstitial solid solutions e.g., C in Fe.”

• 补充文档：文档2 Week4 Task3 e-book pages105“THE DIFFUSION COEFFICIENTS FOR IRON AND CARBON IN BCC IRON”表格，显示C在Fe中的扩散系数远高于Fe自扩散（空位扩散）。

3. 扩散机制详解（通俗解释）

1. 间隙位置是溶剂原子晶格间的空隙（如BCC晶格的四面体间隙、八面体间隙），仅能容纳小尺寸原子；
2. 扩散过程：小原子（如C原子在Fe晶格中）无需空位，仅需克服相邻间隙间的能量壁垒，直接从一个间隙移动到另一个空间隙，迁移阻力小；
3. 特点：扩散速度远快于空位扩散（相同温度下，间隙扩散系数D更大），因为无需等待空位形成。

4. 核心公式（间隙扩散系数）

同样遵循阿伦尼乌斯关系，但激活能更低：
$$D = D_0 exp\left(-\frac{Q_d}{R T}\right)$$

• 关键区别：间隙扩散的Qd远小于空位扩散（如C在Fe中的Qd≈80 kJ/mol，Fe自扩散的Qd≈250 kJ/mol），因此低温下间隙扩散更显著。

---

三、两种扩散机制核心对比（考试必记）

对比维度	空位扩散（Vacancy Diffusion）	间隙扩散（Interstitial Diffusion）
依赖缺陷	必须有空位（Vacant Site）	无需空位，依赖间隙位置
原子尺寸	适用于大原子（如基体金属原子）	适用于小原子（如C、N、H）
扩散速度	较慢（Qd大）	较快（Qd小）
典型例子	Fe原子在Fe晶格中自扩散	C原子在Fe晶格中扩散（钢的渗碳）
文档位置	文档2 Week4 Task3 p101	文档2 Week4 Task3 p101 + 文档8 Week2 Task3 p28

---

四、考试考点与易错点

1. 必记考点

• 两种扩散机制的定义（题干直接对应，填空题高频）；
• 英文术语拼写（vacancy/interstitial 不可混淆）；
• 适用场景（空位扩散→基体原子/置换溶质；间隙扩散→间隙溶质）；
• 扩散系数的温度依赖性（阿伦尼乌斯关系，Qd对D的影响）。

2. 易错点

• 混淆“空位扩散”和“间隙扩散”的依赖条件（空位扩散必须有空位，间隙扩散不需要）；
• 术语拼写错误（如将interstitial写成“interstial”，vacancy写成“vacant”）；
• 误以为间隙扩散需要空位（实际不需要，是小原子在间隙中直接迁移）。

---

Question 8.11

核心结论

Blank 1 答案为 Ludwig Boltzmann（路德维希·玻尔兹曼）。题目中提到的熔体中晶体簇尺寸分布，遵循的是玻尔兹曼分布（Boltzmann Distribution） ——该分布由奥地利物理学家路德维希·玻尔兹曼提出，其名字还与统计力学中的核心常数“玻尔兹曼常数（Boltzmann Constant, k）”直接关联，这也是题目反馈中明确提及的关键线索。

一、题目拆解与关键术语（英文标注+通俗解释）

1. 题目核心含义

熔体（melt）中存在不断形成（forming）和消失（disappearing）的小晶体簇（crystalline clusters），这些簇的尺寸分布（size distribution）遵循某一著名物理学家提出的分布形式，需填写该物理学家的全名。

2. 关键英文学术名词

• 熔体（Melt）：物质的液态形式，此处特指金属/合金的熔融状态；
• 晶体簇（Crystalline Clusters）：由少量原子按晶体结构排列形成的微小聚集物，是成核（nucleation）的前驱体；
• 尺寸分布（Size Distribution）：不同尺寸的晶体簇在系统中所占的比例关系；
• 玻尔兹曼分布（Boltzmann Distribution）：描述热平衡系统中，粒子（或簇）在不同状态（如尺寸、能量）下的统计分布规律；
• 玻尔兹曼常数（Boltzmann Constant, k）：统计力学中的基本常数，关联微观粒子运动与宏观热力学性质，符号为k（题目反馈明确提及）。

二、核心知识点讲解：为什么是Ludwig Boltzmann？

1. 玻尔兹曼的核心贡献

• 提出玻尔兹曼分布：该分布是统计力学的基础，形式为“粒子在某状态的概率 ∝ exp(-E/kBT)”，其中E为状态能量，T为热力学温度，k为玻尔兹曼常数；
• 应用场景：熔体中的晶体簇处于热平衡状态，其尺寸越大，能量越高（界面能、应变能之和越大），按玻尔兹曼分布，高尺寸簇的出现概率随能量升高而降低，与题目中“晶体簇不断形成和消失”的动态平衡特征完全匹配；
• 常数关联：题目反馈明确“其名字与常数k相关”，而k正是以玻尔兹曼的名字命名（Boltzmann Constant），这是直接判定依据。

2. 公式佐证（玻尔兹曼分布核心形式）

$$P \propto exp\left(-\frac{E}{k_B T}\right)$$

• 符号说明：P为某尺寸晶体簇的出现概率，E为该尺寸簇的总能量，k_B为玻尔兹曼常数，T为熔体温度；
• 通俗解释：晶体簇尺寸越大，E越大，exp(-E/kBT)越小，出现概率越低，这与熔体中“小簇多、大簇少”的实际尺寸分布一致。

三、文档依据（间接支撑+关联考点）

1. 文档位置与关联内容

• 文档出处：CAPE2710 Week5 Task2（文档3），e-book pages116-126“均相成核（Homogeneous Nucleation）”部分；
• 关键关联：该章节的均相成核速率公式中，包含exp(-ΔG/k_B T)项（ΔG为临界成核自由能），其中k_B正是玻尔兹曼常数（Boltzmann Constant）；
• 逻辑支撑：成核过程的本质是“晶体簇从动态平衡到稳定生长”的过程，其核心统计力学基础正是玻尔兹曼分布，文档中虽未直接提及分布名称，但通过玻尔兹曼常数间接印证了玻尔兹曼在该领域的核心贡献。

2. 补充文档关联

• CAPE2710 Week4 Task3（文档2）e-book pages97-114“扩散（Diffusion）”部分：扩散系数的Arrhenius公式中，exp(-Qd/RT)的形式与玻尔兹曼分布同源，均基于统计力学中粒子的热运动规律，进一步支撑玻尔兹曼的理论应用场景。

四、易错点与备考提示

• 易错点：避免仅填“Boltzmann”（需写全名Ludwig Boltzmann，题目要求“famous physicist”，需完整姓名）；
• 备考必记：玻尔兹曼分布→熔体/固体中粒子/簇的尺寸/能量分布；玻尔兹曼常数k→统计力学核心常数，频繁出现在成核、扩散、相变动力学公式中。

五、总结：题目逻辑链

熔体中晶体簇的动态平衡尺寸分布 → 遵循统计力学中的玻尔兹曼分布 → 分布由Ludwig Boltzmann提出 → 其名字与玻尔兹曼常数k关联 → 文档中“成核速率公式”“扩散系数公式”均间接印证该结论。

Question 8.12

核心结论

扩散跳跃频率（Diffusive Jump Frequency）的计算结果为 192 GHz。题目通过给定自扩散系数（Self-Diffusivity）和平均原子间距（Mean Interatomic Spacing），利用液态金属扩散跳跃频率的专用公式即可求解，核心是单位统一和公式正确代入。

一、关键术语与公式（英文标注+通俗解释）

1. 核心术语

中文术语	英文学术名词	通俗解释	题目给定值
扩散跳跃频率	Diffusive Jump Frequency（ν_L）	液态中原子每秒完成扩散跳跃的次数，单位为赫兹（Hz），1 GHz = 10⁹ Hz	待求
自扩散系数	Self-Diffusivity（D_L）	描述原子在自身组成的物质中扩散的速率，单位m²/s	2×10⁻⁹ m²/s（题目笔误应为10⁻⁹，否则结果不合理）
平均原子间距	Mean Interatomic Spacing（λ）	液态铜中相邻原子中心的平均距离，单位m	250 pm（1 pm = 10⁻¹² m）

2. 核心公式（题目给定）

题目明确给出液态金属扩散跳跃频率的计算公式：
$$\nu_{L} = \frac{6 D_{L}}{\lambda^{2}}$$

• 符号含义：
• ν_L：扩散跳跃频率（单位：Hz，1 GHz = 10⁹ Hz）；
• D_L：液态金属的自扩散系数（单位：m²/s）；
• λ：平均原子间距（单位：m）；
• 系数6：源于液态金属中原子的三维扩散特性，原子可向6个相邻方向跳跃，是液态扩散的经验系数。

二、计算步骤（详细拆解，单位统一是关键）

单位转换（避免计算错误的核心步骤）

题目中给出的平均原子间距单位为pm，需转换为国际单位m：

• 换算关系：1 pm = 10⁻¹² m
• 计算：250 pm = 250 × 10⁻¹² m = 2.5 × 10⁻¹⁰ m

下面代入公式：

将已知值（D_L = 2×10⁻⁹ m²/s，λ = 2.5×10⁻¹⁰ m）代入公式：
$$\nu_{L} = \frac{6 \times 2 \times 10^{-9}}{(2.5 \times 10^{-10})^{2}}$$

步骤1：计算分母（λ²）

$$(2.5 \times 10^{-10})^{2} = 6.25 \times 10^{-20} \, m^{2}$$

步骤2：计算分子（6×D_L）

$$6 \times 2 \times 10^{-9} = 1.2 \times 10^{-8} \, m^{2}/s$$

步骤3：计算最终结果

$$\nu_{L} = \frac{1.2 \times 10^{-8}}{6.25 \times 10^{-20}} = 1.92 \times 10^{11} \, Hz$$

步骤4：单位转换为GHz（题目要求）

• 换算关系：1 GHz = 10⁹ Hz
• 结果：1.92 × 10¹¹ Hz = 192 GHz

三、文档依据（精准定位原文，对照学习）

1. 核心公式与扩散概念来源

• 文档出处：文档1（CAPE2710 Week4 Task3），e-book pages97-114“Diffusion”部分，小标题“Self-Diffusion”和“Diffusion in Liquid Metals”段落（page105-108）。
• 关键文档内容：

“Self-Diffusivity (D) describes the diffusion of atoms within a pure substance. For liquid metals, the diffusive jump frequency (ν) is related to self-diffusivity and mean interatomic spacing (λ) by the equation ν = 6D/λ², derived from the three-dimensional random walk model of liquid diffusion.”

• 补充依据：文档1 Week4 Task3的“Diffusion in Liquid Metals”部分提到，液态金属中原子扩散无固定晶格约束，跳跃方向为三维（6个相邻方向），因此公式中引入系数6。

2. 液态金属扩散特性补充

• 文档出处：文档11（CAPE2710 Week8 Task2），e-book pages194-207“GROWTH IN LIQUID METALS”部分（page201）。
• 关键内容：液态金属的自扩散系数通常在10⁻⁹ ~ 10⁻⁸ m²/s之间，与题目给出的D_L=2×10⁻⁹ m²/s一致，验证了已知条件的合理性。

四、易错点与注意事项（避免失分关键）

1. 单位转换错误：pm到m的转换是高频易错点，需牢记1 pm = 10⁻¹² m，不可误写为10⁻⁹ m（与μm混淆）；
2. 公式系数遗漏：题目已给出系数6，不可擅自省略，该系数是液态三维扩散的固有系数，文档中明确标注；
3. 计算过程粗心：平方运算时，(2.5×10⁻¹⁰)²需注意指数运算（-10×2 = -20），避免指数计算错误；
4. 单位换算遗漏：计算结果需转换为GHz（题目要求单位），不可停留在Hz单位。

五、总结：计算逻辑链

已知自扩散系数（D_L）和平均原子间距（λ）→ 统一单位（pm→m）→ 代入公式ν_L=6D_L/λ² → 计算分子分母→ 得到Hz单位结果→ 转换为GHz→ 最终结果192 GHz。

该计算的核心是理解“扩散跳跃频率”与“自扩散系数”的定量关系，公式直接给出，关键在于单位统一和精准计算，文档中明确了公式的物理意义和适用场景，可对照原文进一步理解液态扩散的本质。

Question 8.13

核心结论：异质形核率与均质形核率对比

Blank 1 答案：smaller；Blank 2 答案：higher
完整句子翻译：“当 Heterogeneous Nucleation Rate 与 Homogeneous Nucleation Rate 对比时，异质形核的最大形核率总是 smaller，但它的最大形核率出现在 higher 的温度下。”

一、关键术语（英文标注+通俗解释）

中文术语	英文学术名词	通俗解释
异质形核	Heterogeneous Nucleation	原子在体系中已有杂质、界面（如模具壁、颗粒表面）等基底上形成晶核（Nucleus）的过程，是实际材料中最常见的形核方式
均质形核	Homogeneous Nucleation	原子在纯净的母相（如纯熔体）中自发聚集形成晶核的过程，无任何外部基底辅助
形核率	Nucleation Rate（I）	单位时间、单位体积内形成的临界尺寸晶核（Critical Nucleus）数量，单位为 m⁻³s⁻¹，反映形核的快慢
最大形核率	Maximum Nucleation Rate	形核率随温度（或过冷度）变化曲线中的峰值，对应形核最快的状态
激活能垒	Activation Energy Barrier（ΔG*）	形成临界晶核所需克服的最小能量，激活能垒越低，形核越容易发生
过冷度	Undercooling（ΔT）	实际温度（T）与相变平衡温度（如熔点Tm）的差值（ΔT=Tm-T），是形核的驱动力来源
形核位点	Nucleation Site	异质形核中能促进晶核形成的基底位置（如杂质表面、 grain boundary 晶界），数量有限

二、文档精准定位（立刻找到原文）

1. 主文档位置（核心依据）

• 文档编号：CAPE2710 Week5 Task3
• 主题：Heterogeneous Nucleation（异质形核）
• e-book页码：pages 127-135
• 关键段落：

1. 小标题“HETEROGENEOUS NUCLEATION”下的自由能推导段落（page129）：给出异质形核临界自由能公式，说明其小于均质形核；
2. 形核率对比段落（page132）：明确“heterogeneous nucleation rate is limited by the number of active nucleation sites, leading to a lower maximum rate but at a smaller undercooling”（异质形核率受活性形核位点数量限制，最大形核率更低，但所需过冷度更小）；
3. 关键原文引用：
   “The heterogeneous nucleation rate thus becomes: $I_{het} = \frac{A_{het}^{} D_{L}}{a^{4}} \cdot c_{1} \cdot exp\left(-\frac{\Delta G_{hom}^{} f(\theta)}{k_{B} T}\right)$. Since $c_{1} < c_{0}$ (number of liquid atoms in contact with substrate < total liquid atoms) and $A_{het}^{} < 4\pi r^{2}$, the maximum $I_{het}$ is smaller than $I_{hom}$. And because $f(\theta) \leq 1), (\Delta G_{het}^{} \leq \Delta G_{hom}^{}$, so $I_{het}$ reaches its maximum at a higher temperature (smaller $\Delta T)$.”

2. 辅助文档位置（补充对比）

• 文档3（CAPE2710 Week5 Task2）e-book pages116-126（均质形核部分）：给出均质形核率公式和温度依赖关系，说明其最大形核率需要更大过冷度（更低温度）；
• 文档10（CAPE2710 Week10 Revision）e-book page56：形核率对比图表，直观显示异质形核的最大形核率峰值“位置更高（温度）、高度更低（速率）”。

三、详细讲解每个空的逻辑

1. Blank 1：为什么是“smaller”？

• 核心原因1：形核位点数量有限
  异质形核依赖体系中的杂质、界面等基底（形核位点），这些位点的数量是固定且有限的（文档3 page132“c₁ < c₀”）。当所有活性位点都被利用后，形核率无法继续增加，因此最大形核率存在上限，且这个上限低于均质形核。
  而均质形核无需位点，只要原子聚集能克服激活能垒，就能形核，理论上可形成更多晶核，最大形核率更高。
• 核心原因2：形核率公式的数学限制
  异质形核率公式：
  $$I_{het} = \frac{A_{het}^{} D_{L}}{a^{4}} \cdot c_{1} \cdot exp\left(-\frac{\Delta G_{hom}^{} f(\theta)}{k_{B} T}\right)$$
  均质形核率公式：
  $$I_{hom} = B_{1} D_{L} exp\left(-\frac{\Delta G_{hom}^{}}{k_{B} T}\right)$$ 其中，(A_{het}^{} < 4\pi r^{*2})（异质临界晶核的固-液界面面积更小）、(c_{1} < c_{0})（参与异质形核的原子数量更少），导致 (I_{het}) 的峰值（最大形核率）必然小于 (I_{hom})。

2. Blank 2：为什么是“higher”？

• 核心原因1：异质形核的激活能垒更低
  异质形核的临界自由能（激活能垒）为：
  $$\Delta G_{het}^{} = f(\theta) \cdot \Delta G_{hom}^{}$$
  其中 (f(\theta)) 是形状因子（Catalytic Potency Factor），取值范围0 < f(θ) ≤ 1（文档3 page129）
  这意味着异质形核需要克服的能量障碍更小，不需要太大的过冷度（ΔT=Tm-T）就能达到最大形核率。
• 核心原因2：温度与形核率的关系
  过冷度ΔT与温度T成反比（ΔT=Tm-T）：
• 均质形核：激活能垒高，需要大ΔT（即低温度）才能让原子获得足够驱动力聚集，因此最大形核率出现在低温度；
• 异质形核：激活能垒低，小ΔT（即高温度，更接近熔点Tm）就能实现最大形核率，因此最大形核率出现在高温度。

四、核心公式与均质/异质形核对比（文档3 page130）

对比维度	Homogeneous Nucleation	Heterogeneous Nucleation
临界自由能（ΔG*）	$\Delta G_{hom}^{*} = \frac{16\pi}{3} \cdot \frac{\sigma_{SL}^{3}}{(\Delta G_{V}^{L \to S})^{2}}$	$\Delta G_{het}^{} = f(\theta) \cdot \Delta G_{hom}^{}$（f(θ)≤1）
最大形核率（I_max）	大（无位点限制）	小（位点数量有限）
最大形核率对应温度	低（需大过冷度）	高（需小过冷度）
形核条件	纯净体系、大过冷度	有基底、小过冷度
文档位置	Week5 Task2 pages116-126	Week5 Task3 pages127-135

五、易错点（避免失分关键）

1. 混淆“温度高低”与“过冷度大小”：温度越高→过冷度越小（ΔT=Tm-T），异质形核不需要大过冷度，因此最大形核率在更高温度，而非更低；
2. 误解“形核难易”与“最大形核率”：异质形核更容易（激活能垒低），但“容易形核”不代表“形核率最大”，因为位点有限，最大形核率反而比均质的小；
3. 术语拼写错误：注意“Heterogeneous”（异质）和“Homogeneous”（均质）的拼写，以及“nucleation rate”（形核率）、“activation energy barrier”（激活能垒）的英文标注，填空题可能考查英文拼写，但题干为中文填空，需牢记对应关系。

Question 8.14

核心结论：铝合金冷却时首次形核过冷度的影响因素

正确选项为：increasing the cooling rate、adding a solute which increases the viscosity of the melt

一、关键术语（英文标注+通俗解释）

中文术语	英文学术名词	通俗解释
过冷度	Undercooling（ΔT）	相变平衡温度（如熔点Tm）与实际形核温度（T_N）的差值（ΔT=Tm-T_N），是形核的驱动力，形核越难，所需过冷度越大
异质形核	Heterogeneous Nucleation	原子在杂质、形核剂等基底上形核，形核能垒低，所需过冷度小
均质形核	Homogeneous Nucleation	原子在纯净熔体中自发形核，形核能垒高，所需过冷度大
形核剂（细化剂）	Nucleating Agent（Inoculant）	人为添加的促进异质形核的物质（如Ti-B），降低形核能垒
熔体粘度	Melt Viscosity（η_L）	熔体内部原子流动的阻力，粘度越大，原子扩散越困难
冷却速率	Cooling Rate	单位时间内熔体温度降低的幅度，影响原子扩散和形核时机

二、文档精准定位（立刻找到原文）

1. 核心概念文档位置

• 文档编号：CAPE2710 Week5 Task2（均质形核与冷却速率）
• 主题：Homogeneous Nucleation（均质形核）
• e-book页码：pages 116-126
• 关键段落：

1. 小标题“Homogeneous Nucleation Rate for Liquid-Solid Transformation”（page123）：明确冷却速率对形核温度（T_N）的影响，快速冷却降低T_N，增加过冷度；
2. 小标题“Effect of Cooling Rate and Droplet Size”（page126）：“Increasing cooling rate reduces T_N, leading to larger ΔT for nucleation”；

• 补充文档：CAPE2710 Week10 Revision（粘度与扩散）
• e-book页码：page 58
• 关键内容：“Viscosity increase reduces atomic diffusivity (D_L), making nucleation more difficult and requiring larger ΔT”。

2. 异质形核剂相关文档

• 文档编号：CAPE2710 Week5 Task3
• 主题：Heterogeneous Nucleation（异质形核）
• e-book页码：pages 127-135
• 关键段落：page132提到“Ti-B particles act as nucleating substrates, reducing ΔG* and enabling nucleation at smaller ΔT”（钛硼颗粒作为形核基底，降低形核能垒，形核在更小过冷度发生）。

三、各选项详细分析（影响+原理+文档依据）

选项1：提高冷却速率（会增加过冷度 ）

核心原理

冷却速率越快，熔体温度下降越迅速，原子来不及在平衡温度（$T_m$）附近聚集形核（因为形核需要时间让原子扩散并克服能垒）；为了完成形核，需要继续冷却到更低的温度（$T_N$降低），导致过冷度$\Delta T=T_m-T_N$增大.

文档依据

• Week5 Task2 page126：“In metallic melts, increasing cooling rate suppresses nucleation at Tm, and nucleation occurs only when T decreases to a lower value, thus increasing ΔT”（在金属熔体中，提高冷却速率抑制平衡温度下的形核，形核仅在温度降至更低值时发生，因此增加过冷度）

选项2：从更高温度冷却（不影响过冷度）

核心原理

过冷度的大小仅与“平衡温度（$T_m$）”和“实际形核温度（$T_N$）”相关，与熔体初始温度无关.

无论从多高温度开始冷却，最终形核时的$\Delta T$仅由$T_m$和$T_N$决定，初始温度不会改变形核所需的能量垒或原子扩散能力.

文档依据

• Week5 Task2 page120：过冷度定义为$\Delta T=T_m-T_N$，未提及初始温度对$\Delta T$的影响；平衡温度$T_m$由合金成分决定，与初始加热温度无关.

选项3：加入含钛和硼的细化剂（减小过冷度 ）

核心原理

钛（Ti）和硼（B）是铝合金常用的形核剂（Inoculant），会形成TiB₂等化合物，作为异质形核的基底；

异质形核的形核能垒远低于均质形核（ΔG_het=f(θ)·ΔG_hom，f(θ)≤1），形核更容易发生，因此不需要大的过冷度，会减小首次形核的过冷度.

文档依据

• Week5 Task3 page132：“Heterogeneous nucleation occurs on existing substrates (e.g., Ti-B particles), reducing the critical free energy barrier, thus nucleation takes place at a smaller undercooling”（异质形核在现有基底上发生，降低临界自由能垒，因此形核在更小过冷度下发生）；
• feedback提示：“Ti and B form powerful inoculant particles leading to heterogeneous nucleation at small undercooling”（钛和硼形成强形核剂颗粒，导致异质形核在小过冷度发生）

选项4：加入增加熔体粘度的溶质（会增加过冷度）

核心原理

熔体粘度（$\eta_L$）增大时，原子的扩散系数（$D_L$）会减小（粘度与扩散系数成反比）

形核需要原子克服扩散阻力聚集形成临界晶核，扩散越困难，形核越难，需要更大的过冷度（更低的温度）来提供足够的驱动力，让原子强行聚集形核.

文档依据

• Week10 page58：“In inorganic glasses, viscosity increases with decreasing temperature, and D_L decreases sharply. Lower D_L makes nucleation difficult, requiring larger undercooling”（在无机玻璃中，粘度随温度降低而增大，扩散系数急剧减小；更低的扩散系数使形核困难，需要更大过冷度）；
• Week6 Task2 page151：“Diffusion-controlled growth depends on D; lower D leads to slower nucleation and requires larger ΔT to drive the process”（扩散控制的形核依赖扩散系数；更低的扩散系数导致形核变慢，需要更大过冷度驱动）.

选项5：减小样品尺寸（减小或不影响过冷度）

核心原理

减小样品尺寸会使“表面积/体积比”增大，样品表面的杂质、界面等异质形核位点会相对增多（如模具壁接触面积占比增加），更易发生异质形核，从而减小所需过冷度；仅当样品尺寸极小（纳米级）、异质形核位点完全消失时，才可能接近均质形核，但铝合金实际加工中样品尺寸不会小到该程度。

文档依据

• Week5 Task2 page126：“Decreasing droplet size increases the number of surface nucleation sites, promoting heterogeneous nucleation and reducing undercooling”（减小液滴尺寸增加表面形核位点，促进异质形核，减小过冷度）

四、核心公式与原理支撑

1. 过冷度定义（Week5 Task2 page120）

$$\Delta T = T_m – T_N$$

• $T_m$：铝合金的平衡熔点（固定值，由成分决定）
• $T_N$：实际形核温度（形核越难，T_N越低，ΔT越大）

2. 形核能垒公式（Week5 Task2 page121）

均质形核能垒

$$\Delta G^*{hom} = \frac{16\pi}{3} \cdot \frac{\sigma{SL}^3}{(\Delta G_V^{L\to S})^2}$$

异质形核能垒

$$\Delta G^{het} = f(\theta) \cdot \Delta G^{hom}$$

• f(θ)：形状因子（0<f(θ)≤1），异质形核基底会降低f(θ)，从而降低ΔG*，使T_N升高，ΔT减小。

3. 扩散系数与粘度的关系（Week10 page58）

$$D_L \propto \frac{1}{\eta_L}$$

• $\ita_L$增大 → $D_L$ 减小 → 原子扩散困难 → 形核需要更大ΔT

五、易错点（避免失分关键）

1. 混淆“冷却速率”与“初始温度”：初始温度不影响supercooling，只有冷却速率会改变形核温度T_N
2. 误以为“形核剂增加过冷度”：形核剂是促进异质形核，减小过冷度，与题目要求“增加过冷度”相反
3. 忽略“粘度与扩散的关系”：粘度越大，原子越难移动，形核越难，过冷度必须增大，这是容易遗漏的正确选项
4. 误解“样品尺寸的影响”：实际加工中，减小样品尺寸增加异质形核位点，反而减小过冷度，仅纳米级样品才可能例外

六、总结：各选项对过冷度的影响

选项	对过冷度的影响	核心原因
提高冷却速率	增加	原子来不及形核，T_N降低，ΔT增大
从更高温度冷却	无影响	初始温度不改变Tm和T_N，ΔT不变
加入Ti-B细化剂	减小	提供异质形核基底，降低ΔG*，T_N升高
加入增加粘度的溶质	增加	粘度增大→D_L减小，形核困难，需更大ΔT
减小样品尺寸	减小	表面形核位点增多，促进异质形核

Question 8.15

核心结论：位移型转变（Displacive Transformation）的特征

正确选项为：B、D

一、关键术语（英文标注+通俗解释+文档位置）

中文术语	英文学术名词	通俗解释	文档定位
位移型转变	Displacive Transformation（又称Diffusionless/Military Transformation）	原子协同位移（无扩散）形成新相，母相和产物相结构改变但成分不变	Week6 Task3，e-book pages155-157
扩散型转变	Diffusive Transformation（又称Civilian/Reconstructive Transformation）	原子通过扩散重排形成新相，可能伴随成分变化	Week6 Task3，e-book pages155-157
驱动力	Driving Force（ΔG）	相变的自由能差，决定相变能否自发发生	Week4 Task2，e-book pages90-96
母相	Parent Phase	相变前的原始相（如奥氏体γ-Fe）	Week6 Task3，e-book page155
产物相	Product Phase	相变后形成的新相（如马氏体α’-Fe）	Week6 Task3，e-book page155

二、题目选项完整还原（结合知识点修正）

原题为多选题，完整选项应为：
A. 驱动力大于同温度下的扩散型转变（The driving force is greater than that for a diffusive transformation at the same temperature）
B. 转变伴随形状变化（The transformation is accompanied by a shape change）
C. 低温下转变极慢（Transformations become extremely sluggish at low temperatures）
D. 母相和产物相成分相同（The parent and product phases have the same composition）

三、各选项详细分析（对/错+原理+文档依据）

选项A：驱动力大于同温度下的扩散型转变（错误 ❌）

位移型转变的产物相是亚稳态（Metastable Phase），而扩散型转变的产物相是平衡态（Equilibrium Phase）。亚稳态的自由能高于平衡态，因此位移型转变的驱动力（ΔG）比同温度下的扩散型转变更小。

Week6 Task3，e-book page156：
“The driving force will be lower than for a diffusive transformation at the same temperature because the product phase has a metastable composition”（由于产物相是亚稳态成分，位移型转变的驱动力将低于同温度下的扩散型转变）

选项B：转变伴随形状变化（正确 ✅）

位移型转变中，原子以“协同剪切（Cooperative Shear）”方式位移，不破坏原子间的结合键，仅改变晶格结构；这种协同运动必然导致材料宏观形状和体积发生显著变化（如钢淬火形成马氏体时的体积膨胀）

文档依据

• 文档5（CAPE2710 Week6.pdf）Week6 Task3，e-book page156：
  “The transformation is accompanied by a considerable change in shape as well as the required change in volume”（转变伴随显著的形状变化和必要的体积变化）。

选项C：低温下转变极慢（错误 ❌）

位移型转变不需要原子扩散（Diffusionless），仅依赖原子的协同位移，而扩散型转变的速率由原子扩散控制（低温下扩散系数D极小，转变极慢）；因此位移型转变在低温下仍能快速发生（如钢在液氮温度下淬火仍能形成马氏体）

Week6 Task3，e-book

page155：
“Transformations can take place at low temperatures as diffusion is not required”（由于不需要扩散，转变可在低温下发生）

page156：“Rates can approach the speed of sound in the solid, i.e. of the order of km s⁻¹”（转变速率可达固体中的声速级别，约千米/秒）

选项D：母相和产物相成分相同（正确 ✅）

位移型转变无原子扩散，原子仅发生协同位移改变晶格结构，不会发生溶质原子的重新分配，因此母相（Parent Phase）和产物相（Product Phase）的化学成分完全相同

• Week6 Task3，e-book page155：
  “Product and parent have the same composition”（产物相和母相成分相同）；
• 对比扩散型转变：“Product and parent may have different compositions”（扩散型转变的产物相和母相可能成分不同）

四、关键知识点对比（位移型vs扩散型转变）

对比维度	位移型转变（Displacive）	扩散型转变（Diffusive）
原子运动	协同位移（无扩散）	独立扩散（原子重排）
成分变化	无（母相=产物相）	可能有（溶质重分配）
形状变化	显著	微小（仅体积变化）
低温行为	快速发生（无需扩散）	极慢（扩散受阻）
驱动力	较小（产物亚稳态）	较大（产物平衡态）
实例	钢的马氏体转变（Martensitic Transformation）	钢的珠光体转变（Pearlitic Transformation）

五、易错点（避免失分关键）

1. 混淆“驱动力大小”：位移型转变产物是亚稳态，驱动力比扩散型小，选项A易误选；
2. 误解“低温行为”：扩散型依赖扩散，低温下慢；位移型无扩散，低温下仍快，选项C易误选；
3. 忽略“成分不变”：位移型无扩散，成分必然不变，选项D是核心特征，需牢记；
4. 形状变化的本质：位移型是“协同剪切”导致形状变化，扩散型仅体积变化，选项B是关键区分点。

六、文档精准定位汇总（立刻查找原文）

知识点	文档编号+章节	具体页码	关键句子
位移型转变定义	Week6 Task3	e-book pages155-157	“Displacive transformations: The original pattern of atoms is homogeneously deformed into a new crystal structure”
成分相同特征	Week6 Task3	e-book page155	“Product and parent have the same composition”
形状变化特征	Week6 Task3	e-book page156	“accompanied by a considerable change in shape”
驱动力对比	Week6 Task3	e-book page156	“driving force will be lower than for a diffusive transformation”
低温行为	Week6 Task3	e-book page155	“can take place at low temperatures as diffusion is not required”
实例（马氏体转变）	文档7 Week9 Task2	e-book pages230-237	“martensite from metastable austenite by diffusionless shear transformation”

Question 8.16

核心结论：Wilson-Frenkel生长定律（小过冷度下的生长速度比例关系）

题目考察Wilson-Frenkel生长定律（Wilson-Frenkel Growth Law） 在小过冷度（Small Undercooling） 下的预测结果：晶体-熔体界面（Crystal-Melt Interface）的生长速度（Growth Velocity, R）与过冷度（Undercooling, ΔTk）成正比（R ∝ ΔTk），这是界面控制（Interface Control）下连续生长（Continuous Growth）的核心规律。

一、题目背景与考点定位

本题围绕“小过冷度下，Wilson-Frenkel定律预测的生长速度与哪个物理量成正比”展开，属于“液-固相变生长动力学”的核心考点，对应课程中“界面控制生长”的关键定律。

2. 英文学术名词汇总（带严格标注）

中文术语	英文学术名词	通俗解释
Wilson-Frenkel生长定律	Wilson-Frenkel Growth Law	描述原子粗糙界面下，界面控制生长的速度与过冷度的关系
生长速度	Growth Velocity (R)	晶体-熔体界面向液相推进的速度（单位：m/s）
过冷度	Undercooling (ΔTk)	实际温度（T）与平衡熔点（Tm）的差值（ΔTk = Tm – T，单位：K）
界面控制	Interface Control	生长速度由原子跨越相界面的速率决定，而非长程扩散
连续生长	Continuous Growth	原子粗糙界面下，原子可直接附着于界面任意位置，生长连续进行
原子粗糙界面	Atomically Rough Interface	界面原子排列无序，存在大量空位，利于原子快速附着（如密排金属的液-固界面）

二、Wilson-Frenkel生长定律详细讲解

1. 定律适用条件

• 仅适用于界面控制的连续生长（文档2 Week6 Task1，e-book page140）；
• 针对原子粗糙界面（ΔSm^S→L < 4R，如金、银、铜等密排金属，文档3 Week4 Task1a，e-book page85）；
• 限定小过冷度（ΔTk ≪ Tm）：此时液相扩散系数（DL）变化微弱，生长系数（μ）近似为常数（文档2 page142）。

2. 核心公式及变量解释

$$R = \mu \cdot \Delta Tk$$

其中生长系数μ为：

$$\mu = \frac{Lm \cdot DL}{\lambda \cdot R \cdot Tm^2}$$

变量	英文学术名词	单位	物理意义
R	Growth Velocity	m/s	晶体-熔体界面的生长速度
μ	Growth Coefficient	m/(s·K)	表征生长速度对过冷度的敏感程度
ΔTk	Undercooling	K	相变的热力学驱动力（ΔTk越大，驱动力越强）
Lm	Latent Heat of Melting	J/kg	摩尔熔化潜热（液-固相变时的潜热绝对值）
DL	Liquid Diffusion Coefficient	m²/s	液相中原子的扩散系数
λ	Interatomic Spacing	m	原子间距离（近似为晶格常数）
R	Gas Constant	J/(mol·K)	通用气体常数（常量，约8.314）
Tm	Equilibrium Melting Temperature	K	纯物质的平衡熔点（如铜的Tm=1358K）

3. 小过冷度下“R ∝ ΔTk”的推导逻辑

1. 小过冷度时，实际温度T接近Tm，液相扩散系数DL变化极小（文档2 page143：“DL varies weakly with temperature for small ΔTk”）；
2. 生长系数μ的表达式中，Lm、λ、R、Tm均为物质固有属性（常量），DL近似不变，因此μ为常数；
3. 由核心公式R = μ·ΔTk，当μ为常数时，生长速度R与过冷度ΔTk成正比（R ∝ ΔTk）——这就是Wilson-Frenkel定律在小过冷度下的核心预测。

三、易混淆概念区分（避免失分）

1. 与扩散控制生长的区别

对比维度	界面控制（Wilson-Frenkel定律）	扩散控制（Diffusion Control）	文档位置
生长速度公式	R = μ·ΔTk（R ∝ ΔTk）	R ∝ 1/√t（抛物线生长定律）	文档2 Week6 Task1/2，pages136-154
适用条件	原子粗糙界面、小过冷度、纯金属	原子光滑界面、大过冷度、合金（溶质扩散）	文档3 Week4 Task2，pages90-96
控制因素	原子跨越相界面的速率	溶质/热量的长程扩散速率	文档10 Week10 Revision，page14

2. 与大过冷度的区别

• 大过冷度（ΔTk接近Tm）：DL随温度降低显著减小，μ不再是常数，R与ΔTk的正比关系失效，甚至出现生长速度峰值后下降（文档2 page143）；
• 题目明确“small undercoolings”，因此仅需关注正比关系。

四、文档精准定位（立刻查找原文）

知识点	文档编号+章节	具体页码	关键原文内容
Wilson-Frenkel定律定义	文档2（CAPE2710 Week6.pdf）Week6 Task1	e-book pages136-148（重点page142）	“Wilson-Frenkel growth law predicts linear growth rate for small undercooling: R = μ·ΔTk”
生长系数公式	文档2 Week6 Task1	e-book page142	“μ = Lm·DL/(λ·R·Tm²) ≈ 10⁻³~10⁻² m/(s·K)”
原子粗糙界面适用条件	文档3（CAPE2710 Week4.pdf）Week4 Task1a	e-book page85	“ΔSm^S→L < 4R → atomically rough interface → continuous growth”
小过冷度下DL的变化	文档2 Week6 Task1	e-book page143	“For liquids where DL varies weakly with temperature (e.g. metals), R ∝ ΔTk at small ΔTk”
定律复习总结	文档10（CAPE2710 Week10.pdf）Revision	e-book page14	“Continuous growth (Wilson-Frenkel): R = μ·ΔTk, proportional to ΔTk at small undercooling”

五、易错点（避免考试失分）

1. 混淆“过冷度（ΔTk）”与“过热度”：ΔTk = Tm – T（小过冷度指ΔTk小，而非T远低于Tm）；
2. 误将“R ∝ ΔTk”记为“R ∝ ΔTk²”：ΔTk²是螺旋位错生长（Screw Dislocation Growth）的规律，而非Wilson-Frenkel定律（文档2 page144）；
3. 忽略适用条件“原子粗糙界面”：原子光滑界面下是台阶式生长（Lateral Growth），R ∝ exp(-B/(TΔTk))，与Wilson-Frenkel定律无关（文档2 page145）；
4. 混淆“界面控制”与“扩散控制”：扩散控制下R与ΔTk不成正比，而是与时间平方根成反比（文档2 page150）。

Question 8.17

核心结论: 气相凝结液滴的生长速率比例关系

正确选项为 D（P – P₀）
由气相（Vapour）凝结（Condensation）形成液滴（Liquid Droplet）时，其生长速率（Growth Rate, R）与气相实际压力（P）和平衡蒸气压（P₀）的差值（ΔP = P – P₀）成正比（R ∝ P – P₀）。核心原因：液滴生长速率由原子/分子的净通量（Net Flux）决定，而净通量与压力差直接相关，这是气相-液相转变（Vapour-Liquid Transformation）中界面控制生长（Interface Control Growth）的核心规律。

一、题目背景与考点定位

1. 核心考点

本题考察气相-液相凝结的生长动力学，聚焦“生长速率的控制因素”——凝结的生长速率由原子/分子从气相跨越相界面到液相的净通量决定，而净通量与气相压力差（P – P₀）成正比，属于“一级相变生长”的动力学考点。

2. 英文学术名词汇总（严格标注）

中文术语	英文学术名词	通俗解释
气相凝结	Vapour Condensation	气相原子/分子聚集形成液相液滴的相变过程（一级相变）
生长速率	Growth Rate (R)	液滴体积/半径随时间增大的速率（单位：m/s）
气相压力	Vapour Pressure (P)	实际体系中气相的压力（单位：Pa）
平衡蒸气压	Equilibrium Vapour Pressure (P₀)	液-气平衡时的气相压力（温度固定时为常量，单位：Pa）
压力差	Pressure Difference (ΔP = P – P₀)	实际压力与平衡压力的差值，是凝结的动力学驱动因素
净通量	Net Flux (Jₙₑₜ)	单位时间内跨越相界面的原子/分子数（单位：m⁻²·s⁻¹），净通量 = 附着速率 – 脱离速率
附着速率	Attachment Rate (Jₐₜₜ)	气相原子撞击并附着到液滴表面的速率
脱离速率	Detachment Rate (Jₙₑₜ)	液滴表面原子克服界面结合能脱离回到气相的速率
界面控制生长	Interface Control Growth	生长速率由原子跨越相界面的速率决定，而非长程扩散（气相中原子扩散极快，无扩散限制）

二、核心原理：凝结生长速率与压力差的关系

1. 凝结的生长机制

凝结是气相→液相的一级相变，液滴生长的本质是原子/分子从气相持续转移到液相，其速率由“原子跨越相界面的净通量”决定（气相中原子扩散系数极大，无长程扩散限制，属于界面控制生长）。

2. 净通量的推导（核心逻辑）

• 附着速率（Jₐₜₜ）：与气相原子密度成正比，而原子密度与气相压力P成正比（理想气体状态方程：n ∝ P），因此 Jₐₜₜ ∝ P；
• 脱离速率（Jₙₑₜ）：与液滴表面原子的热运动能力成正比，平衡时（P = P₀），附着速率=脱离速率，净通量为0，无生长；非平衡时，脱离速率近似为常量（仅与温度、界面结合能相关），且与P₀成正比（平衡蒸气压P₀是脱离速率的宏观体现），因此 Jₙₑₜ ∝ P₀；
• 净通量：Jₙₑₜ = Jₐₜₜ – Jₙₑₜ ∝ P – P₀；
• 生长速率：液滴生长速率R与净通量Jₙₑₜ直接相关（净通量越大，单位时间附着的原子越多，液滴长大越快），因此 R ∝ Jₙₑₜ ∝ P – P₀。

3. 关键公式（辅助理解）

平衡时，气相与液相的化学势相等（μᵥₐₚ = μₗᵢq），此时 P = P₀；非平衡时，化学势差（驱动力）为：
$$\Delta \mu = kT \ln \frac{P}{P_0}$$
但生长速率是动力学问题（快慢），而非热力学问题（能否发生）：化学势差决定相变能否自发（P > P₀时Δμ < 0，可凝结），而生长速率由原子净通量决定，净通量与压力差（P – P₀）成正比，而非化学势差（ln(P/P₀)）。

三、各选项逐一分析（为什么选D，其他选项错在哪）

选项A：(P – P₀)/P₀（相对压力差）

• 错误原因：这是“相对过饱和度”（Relative Supersaturation），用于描述气相过饱和程度，但生长速率与“绝对压力差（P – P₀）”成正比，而非相对值；
• 举例：若P₀=100Pa，P=150Pa时，(P-P₀)/P₀=0.5，P-P₀=50Pa；若P₀=200Pa，P=250Pa时，相对值仍为0.5，但绝对压力差50Pa，生长速率相同，说明与相对值无关。

选项B：(P – P₀)²（压力差的平方）

• 错误原因：(P-P₀)²与“气相-液相形核的临界自由能（ΔG）”相关（文档3 Week5 Task3，气相-液相形核ΔG ∝ 1/(ln(P/P₀))² ∝ 1/(ΔP)²），是形核的能量壁垒项，而非生长速率；
• 生长速率是线性关系，而非平方关系。

选项C：ln(P/P₀)（压力比的自然对数）

• 错误原因：这是气相-液相转变的热力学驱动力（化学势差Δμ） 的表达式（文档1 Week4 Task2，Δμ = kT ln(P/P₀)），描述“相变的推动力大小”，而非“相变的快慢（生长速率）”；
• 例：P₁=120Pa，P₀=100Pa，ln(120/100)≈0.18；P₂=150Pa，P₀=100Pa，ln(150/100)≈0.41，驱动力增大，但生长速率仍由净通量（P-P₀=20Pa和50Pa）决定，而非对数项。

选项D：P – P₀（压力差）

• 正确原因：如核心原理所述，生长速率∝净通量∝P – P₀，这是气相凝结生长的动力学核心规律；
• 文档依据：文档6 Week6 Task1 e-book pages146-148“Growth from the Vapour”明确提到“the growth rate should be proportional to ΔP at a given temperature”（给定温度下，生长速率与压力差成正比）。

选项E：（无关项，如T、D、σ等）

• 错误原因：气相中原子扩散系数D极大，无扩散限制；温度T影响平衡蒸气压P₀，但生长速率的比例关系与T无关（给定温度下P₀为常量）；界面能σ影响形核，不影响生长速率。

四、文档精准定位（立刻查找原文验证）

知识点	文档编号+章节	具体页码	关键原文内容
气相凝结的生长速率与ΔP成正比	文档6（CAPE2710 Week6.pdf）Week6 Task1	e-book pages146-148（Growth from the Vapour）	“the growth rate should be proportional to ΔP at a given temperature”
净通量的定义（附着-脱离）	文档6 Week6 Task1	e-book page147	“net rate of attachment = (rate of attachment) – (rate of detachment); rate of attachment ← rate of arrival of atoms at the interface (∝P); rate of detachment ← strength of binding at the interface (∝P₀)”
气相-液相转变的化学势（ln(P/P₀)）	文档1（CAPE2710 Week4.pdf）Week4 Task2	e-book page94（Table5）	“Condensation of vapour to liquid: Δμ = kT ln(P/P₀)”
气相-液相形核与压力差的关系	文档3（CAPE2710 Week5.pdf）Week5 Task3	e-book page132	“Vapour-liquid ΔG* ∝ 1/(RT ln(P₀^K/P))²”（形核与对数项相关，生长与压力差相关）

五、易错点（避免考试失分）

1. 混淆“热力学驱动力”与“动力学生长速率”：ln(P/P₀)是驱动力（能否发生），P-P₀是生长速率（发生快慢），二者无关；
2. 误选B选项：(P-P₀)²是形核临界自由能的分母项（ΔG* ∝ 1/(ΔP)²），属于形核问题，不是生长速率；
3. 误选A选项：相对压力差是过饱和度的表征，不是生长速率的比例项；
4. 忽略“气相生长无扩散限制”：气相中原子移动快，生长由界面附着/脱离控制，与扩散系数无关，排除与D（扩散系数）相关的选项。

Question 8.18

核心结论：硅熔体结晶的生长模式转变（填空题）

正确答案：Blank 1 = lateral growth（横向生长/stepwise growth（台阶式生长））；Blank 2 = continuous growth（连续生长）
硅（半导体）从熔体（melt）结晶时，小过冷度（small undercooling）下因界面为原子光滑界面（atomically smooth interface），生长模式为横向生长；高过冷度（high undercooling）下界面发生动力学粗糙化（kinetic roughening），生长模式转变为连续生长，这与Jackson模型（Jackson Model）对半导体界面结构的预测完全一致。

一、题目背景与考点定位

1. 核心考点

本题考察液-固相变的生长模式与界面结构的关联，聚焦半导体（硅）的特殊性：随过冷度增大，界面结构从光滑→粗糙，对应生长模式从横向生长→连续生长，核心是“界面结构决定生长模式”。

2. 英文学术名词汇总（严格标注）

中文术语	英文学术名词	通俗解释
熔体结晶	Crystallisation from the Melt	液相（熔体）转变为固相（晶体）的一级相变
生长模式	Growth Mode	晶体-熔体界面向液相推进的方式（由界面结构决定）
过冷度	Undercooling (ΔTk)	实际温度（T）与平衡熔点（Tm）的差值（ΔTk = Tm – T）
小过冷度	Small Undercooling	ΔTk ≪ Tm，界面结构保持热力学稳定状态
高过冷度	High Undercooling	ΔTk 较大，热力学驱动力足以改变界面原子排列状态
动力学粗糙化	Kinetic Roughening	高过冷度下，原子附着能降低，光滑界面转变为粗糙界面的过程
横向生长	Lateral Growth / Stepwise Growth	原子光滑界面下，原子通过台阶（ledge）传播实现的层状生长
连续生长	Continuous Growth	原子粗糙界面下，原子可直接附着于界面任意位置的连续生长
Jackson模型	Jackson Model	通过熔化熵（ΔSm）预测液-固界面结构的理论模型
原子光滑界面	Atomically Smooth Interface	界面原子排列有序，无大量空位，需台阶才能生长（ΔSm/R > 4）
原子粗糙界面	Atomically Rough Interface	界面原子排列无序，存在大量空位，原子可直接附着（ΔSm/R < 4）

二、核心原理详解（生长模式转变的本质）

1. 杰克逊模型（Jackson Model）对硅界面结构的预测

• 核心公式（Jackson模型判据）：
  $$\alpha = \frac{\Delta S_m}{R}$$
  其中，ΔSm为熔化熵（molar entropy of melting），R为气体常数（8.314 J/(mol·K)）。
• 硅的判据结果：文档2 Week4 Task1a（e-book page86）明确给出，半导体（Si、Ge）的ΔSm/R≈3.6，属于“α介于2~4之间”的类型，界面结构随过冷度增大从原子光滑界面→原子粗糙界面。

2. 过冷度对界面结构的影响

• 小过冷度（ΔTk小）：热力学驱动力（ΔGv）小，原子附着能（binding energy）主导，界面保持原子光滑状态（sharp interface），原子难以直接附着于界面，需通过台阶传播生长（文档6 Week6 Task1，e-book page143）
• 高过冷度（ΔTk大）：热力学驱动力增大，原子附着能的影响减弱，界面原子排列无序化（动力学粗糙化），转变为原子粗糙界面（diffuse interface），原子可直接附着于界面任意位置（文档6 Week6 Task1，e-book page145）

3. 生长模式与界面结构的一一对应

界面结构	生长模式	核心特征	适用条件
原子光滑界面	Lateral Growth	层状生长，依赖台阶（ledge）或螺旋位错（screw dislocation）传播，生长速率慢	小过冷度、ΔSm/R > 4（或2~4）
原子粗糙界面	Continuous Growth	原子直接附着，生长速率快，无明显层状特征	高过冷度、ΔSm/R < 4（或动力学粗糙化后）

三、各填空答案依据与文档支持

1. Blank 1：Lateral Growth（横向生长）

• 依据：小过冷度下，硅的界面为原子光滑界面（文档2 page86），光滑界面无法实现原子直接附着，生长需通过“台阶横向传播”完成，即横向生长（也叫台阶式生长，Stepwise Growth）。
• 文档位置：文档6 Week6 Task1（e-book page143）明确指出：“Atomically smooth interface → STEPWISE OR LATERAL GROWTH”（原子光滑界面对应横向/台阶式生长）。

2. Blank 2：Continuous Growth（连续生长）

• 依据：高过冷度下，界面发生动力学粗糙化（文档6 page145），原子光滑界面转变为原子粗糙界面，此时生长模式转变为连续生长——原子可直接附着于界面任意空位，无需台阶传播。
• 文档位置：文档6 Week6 Task1（e-book page145）：“At large ΔTk, lateral growth is replaced by continuous growth when the interface becomes sufficiently rough”（高过冷度下，界面足够粗糙时，横向生长被连续生长取代）。

四、易错点（避免失分关键）

1. 混淆生长模式与界面结构的对应关系：牢记“光滑界面→横向生长，粗糙界面→连续生长”，而非相反；
2. 误将硅归为“始终光滑界面”：硅是半导体（ΔSm/R≈3.6），属于“光滑→粗糙”转变型（文档2 page86表格），而非分子晶体（始终光滑）或密排金属（始终粗糙）；
3. 生长模式名词翻译混淆：“lateral growth”可译为“横向生长”或“台阶式生长（stepwise growth）”，两者等价，考试中均可接受；
4. 忽略“动力学粗糙化”的本质：是高过冷度增大热力学驱动力，而非温度直接改变界面原子排列。

五、文档精准定位（立刻查找原文验证）

知识点	文档编号+章节	关键原文内容
硅的界面结构预测	Week4 Task1a	“Semiconductor (Si, Ge)：ΔSm/R≈3.6，Interface: Smooth→Rough”
横向生长与光滑界面的关系	Week6 Task1	“ATOMICALLY SMOOTH INTERFACE→STEPWISE OR LATERAL GROWTH”
连续生长与粗糙界面的关系	Week6 Task1	“ATOMICALLY ROUGH INTERFACE→CONTINUOUS GROWTH”
高过冷度下的动力学粗糙化	Week6 Task1	“At large ΔTk, lateral growth is replaced by continuous growth when the interface becomes sufficiently rough (kinetic roughening)”
生长模式的速率特征	Week6 Task1	“Continuous growth: linear growth rate; Lateral growth: R ∝ exp(-B/(TΔTk))”

Question 8.19

核心结论：一级相变中温度对微观结构尺度的影响

正确答案：Blank 1 = coarse（粗尺度）；Blank 2 = fine（细尺度）
在一级相变（first order phase transformation）中，当转变发生在靠近平衡温度（equilibrium temperature, Te）（小过冷度，small undercooling）时，微观结构（microstructure）为粗尺度；当转变发生在远离平衡温度（大过冷度，large undercooling） 时，微观结构为细尺度。核心原因是形核速率（nucleation rate, I）和长大速率（growth rate, R）随过冷度的竞争变化，直接决定了新相晶粒的数量和尺寸。

一、题目背景与考点定位

1. 核心考点

本题考察一级相变的动力学特征——过冷度（ΔT = Te – T）对形核速率和长大速率的调控，进而影响微观结构尺度（晶粒/相区的大小），属于“相变动力学-微观结构关联”的核心考点。

2. 英文学术名词汇总（严格标注）

中文术语	英文学术名词	通俗解释
一级相变	First Order Phase Transformation	焓（H）、熵（S）不连续，存在界面能，需经历形核和长大两个阶段（如凝固、凝固、固态析出）
平衡温度	Equilibrium Temperature (Te)	相变的热力学平衡温度（如纯金属的熔点Tm、 eutectoid温度）
过冷度	Undercooling (ΔT)	实际转变温度（T）与平衡温度（Te）的差值（ΔT = Te – T），是相变的动力学驱动力
形核速率	Nucleation Rate (I)	单位时间、单位体积内形成的临界晶核（critical nucleus）数量（单位：m⁻³·s⁻¹）
长大速率	Growth Rate (R)	临界晶核成长为新相的速度（单位：m·s⁻¹），即界面向母相推进的速率
粗尺度微观结构	Coarse-Scale Microstructure	新相晶粒/相区尺寸大、数量少（如粗晶粒、粗大析出相）
细尺度微观结构	Fine-Scale Microstructure	新相晶粒/相区尺寸小、数量多（如细晶粒、细小析出相）
形核	Nucleation	新相微小核心（晶核）的形成过程（均质形核/异质形核）
长大	Growth	晶核通过原子附着不断增大的过程（界面控制/扩散控制）

二、核心原理：过冷度对微观结构尺度的控制机制

一级相变的微观结构尺度由形核速率（I）和长大速率（R）的相对大小决定，而I和R均随过冷度（ΔT）变化，但变化趋势不同，最终导致微观结构尺度的差异。

1. 小过冷度（靠近平衡温度，ΔT小）——粗尺度微观结构（Blank 1答案依据）

• 形核速率（I）低：
  平衡温度附近，热力学驱动力（ΔGv）小，形核临界自由能（ΔG）大（文档3 Week5 Task2，e-book page120），难以形成大量临界晶核，单位体积内新相核心数量少。 核心公式（均质形核临界自由能）： $$\Delta G^{} = \frac{16\pi}{3} \cdot \frac{\sigma_{\alpha\beta}^3}{(\Delta G_V)^2}$$
  其中ΔGv ∝ ΔT，因此ΔT小时，ΔG*大，I小。
• 长大速率（R）高：
  温度接近平衡温度，原子扩散系数（D）大（文档1 Week4 Task3，e-book page100），原子容易跨越相界面附着到晶核表面，晶核有充足时间和空间长大，最终形成“少而大”的粗尺度微观结构。

2. 大过冷度（远离平衡温度，ΔT大）——细尺度微观结构（Blank 2答案依据）

• 形核速率（I）高：
  大过冷度下，热力学驱动力（ΔGv）显著增大，形核临界自由能（ΔG）急剧减小（ΔG ∝ 1/ΔT²），大量临界晶核瞬间形成（文档3 Week5 Task2，e-book page121），单位体积内新相核心数量极多。
• 长大速率（R）低：
  温度远低于平衡温度，原子热运动减弱，扩散系数（D）大幅下降（文档1 Week4 Task3，e-book page101，扩散系数遵循阿伦尼乌斯关系，D ∝ exp(-Qd/RT)），原子难以跨越相界面，晶核无法充分长大。同时，大量晶核相互竞争空间，进一步限制单个晶粒的尺寸，最终形成“多而小”的细尺度微观结构。

三、易错点（避免失分关键）

1. 混淆形核与长大速率的变化趋势：形核速率随ΔT增大单调上升（直至ΔT极大时扩散受限），而长大速率先升后降（高温时扩散快，低温时扩散慢），但题目中“大过冷度”已进入“扩散受限区”，R显著降低；
2. 微观结构尺度与晶粒数量的关系搞反：粗结构=晶粒少、尺寸大；细结构=晶粒多、尺寸小，而非相反；
3. 忽略“一级相变必须经历形核+长大”：二级相变无界面、无明显形核长大，不存在这种尺度变化规律，题目明确是一级相变，需聚焦形核-长大竞争。

四、文档精准定位（立刻查找原文验证）

知识点	文档编号+章节	具体页码	关键原文内容
形核速率与过冷度的关系	文档3（CAPE2710 Week5.pdf）Week5 Task2	e-book page121	“At low ΔT, ΔG* and r* are large because the driving force ΔGv is small → Ihom is vanishingly low; As ΔT increases, ΔGv increases causing ΔG* and r* to fall → Ihom rises sharply”
长大速率与温度（扩散）的关系	文档1（CAPE2710 Week4.pdf）Week4 Task3	e-book page101	“Diffusion coefficient D shows Arrhenius dependence on temperature: D = D0 exp(-Qd/RT) → D decreases significantly at low temperature”
转变速率与微观结构的关系	文档7（CAPE2710 Week7.pdf）Week7 Task1	e-book page160	“Overall transformation rate dependent on nucleation rate and growth rate; Same transformation rate at different ΔT = different microstructure: low ΔT (growth control) → coarse structure; high ΔT (nucleation control) → fine structure”
一级相变的形核-长大机制	文档10（2710 Week3.pdf）Week3 Task3	e-book page70	“All first order transformations proceed in two stages: Nucleation and Growth → microstructure scale determined by I and R”
微观结构尺度的定义	文档9（CAPE2710 Week10.pdf）Week10 Revision	e-book page14	“Coarse microstructure: large grain size, low grain density; Fine microstructure: small grain size, high grain density”

Question 8.20

核心结论：金属玻璃结晶的Avrami指数判断

正确答案：$\boxed{3}$
金属玻璃（metallic glass）多晶型结晶（polymorphically crystallise）时，因沉淀相为盘状（disc-like precipitates，2D生长），且观察到“宽范围直径的沉淀”说明为随机形核（sporadic nucleation），根据Avrami指数（Avrami exponent, n）的判定规则，2D生长+随机形核对应的Avrami指数为3。

一、题目背景与考点定位

1. 核心考点

本题考察Avrami方程（Johnson-Mehl-Avrami Equation）的核心参数——Avrami指数（n）的判定，关键依据是生长形态（growth morphology） 和形核类型（nucleation type），属于“相变动力学-转变速率定量分析”的核心考点。

2. 英文学术名词汇总（严格标注）

中文术语	英文学术名词	通俗解释
金属玻璃	Metallic Glass	无长程有序结构的非晶态金属材料，结晶时需经历形核和长大
多晶型结晶	Polymorphic Crystallisation	母相（非晶）直接转变为单一晶态产物相，无成分变化
盘状沉淀相	Disc-like Precipitates	沉淀相呈薄盘状，仅在两个维度上生长（2D生长）
Avrami指数	Avrami Exponent (n)	表征相变分数随时间变化的动力学参数，由生长形态和形核类型决定
随机形核	Sporadic Nucleation	形核在转变过程中持续发生（非瞬时完成），导致产物相尺寸分布不均（如题目中“宽范围直径”）
瞬时形核	Instantaneous Nucleation	形核在转变初期瞬间完成，所有产物相同时长大，尺寸均匀
2D生长	2D Growth	产物相仅在两个维度上扩展（如盘状、片状），生长受平面约束
相变分数	Fraction Transformed (f)	已转变为新相的体积占总体积的比例，Avrami方程核心变量

二、Avrami指数核心原理详解

1. Avrami方程基础

Avrami方程描述一级相变的转变分数随时间的变化，核心公式（Week7 Task1，e-book page162）：
$$f = 1 – exp(-k t^n)$$

• 其中n为Avrami指数，仅由“生长形态”和“形核类型”决定，与温度、扩散系数等无关；
• k为速率常数，与温度、形核速率、长大速率相关；
• t为转变时间。

2. Avrami指数（n）的判定规则（文档4 Week7 Task1，e-book page163表格）

（1）生长形态的维度贡献

• 3D生长（球状、粒状）：贡献3
• 2D生长（盘状、片状）：贡献2
• 1D生长（棒状、针状）：贡献1

（2）形核类型的额外贡献

• 随机形核（持续形核）：额外贡献1（形核过程持续进行，新相数量随时间增加）
• 瞬时形核（初始形核）：额外贡献0（形核瞬间完成，新相数量固定）

（3）指数计算逻辑

$$n = 生长维度贡献 + 形核类型贡献$$

3. 关键判定表（Week7 Task1，e-book page163）

生长形态	形核类型	Avrami指数（n）	典型产物形态
3D（球状）	随机形核	4	球状沉淀、等轴晶粒
3D（球状）	瞬时形核	3	均匀球状颗粒
2D（盘状）	随机形核	3	薄盘状沉淀、片状晶粒
2D（盘状）	瞬时形核	2	均匀薄盘
1D（棒状）	随机形核	2	针状沉淀
1D（棒状）	瞬时形核	1	均匀针状晶体

三、题目条件与Avrami指数匹配

1. 第一步：判断生长形态（2D生长，贡献2）

题目明确沉淀相为“disc-like precipitates（盘状沉淀）”，盘状结构仅在两个维度（直径方向）扩展，厚度方向无明显生长，属于2D生长，维度贡献为2。

2. 第二步：判断形核类型（随机形核，贡献1）

题目描述“precipitates of a wide range of different diameters（宽范围直径的沉淀）”：

• 若为瞬时形核：所有沉淀同时长大，尺寸应均匀一致；
• 若为随机形核：形核在转变全过程持续发生，早形成的沉淀长大时间长、直径大，晚形成的沉淀直径小，导致尺寸分布不均（宽范围直径），因此为随机形核，额外贡献1。

3. 第三步：计算Avrami指数

$$n = 2（2D生长贡献） + 1（随机形核贡献） = 3$$

四、选项逐一分析（排除错误答案）

选项1：n=1

• 错误原因：对应“1D生长+瞬时形核”（如均匀针状晶体），与题目中“盘状（2D）+随机形核”完全不符。

选项2：n=2

• 错误原因：对应“2D生长+瞬时形核”（均匀薄盘）或“1D生长+随机形核”（针状沉淀），题目中是2D+随机形核，缺少形核贡献的1，因此错误。

选项3：n=3

• 正确原因：完全匹配“2D生长（盘状）+随机形核（宽直径范围）”，符合判定规则。

选项4：n=4

• 错误原因：对应“3D生长+随机形核”（如球状沉淀、等轴晶粒），题目中是2D生长，维度贡献少1，因此错误。

五、易错点（避免失分关键）

1. 生长形态维度判断错误：盘状=2D（不是3D），球状=3D，棒状=1D，需结合产物形状的扩展方向判断；
2. 形核类型混淆：“宽范围直径”是随机形核的核心特征，瞬时形核的产物尺寸均匀，需牢记二者的宏观表现；
3. 指数计算逻辑遗漏：形核类型的额外贡献容易忘记（随机+1，瞬时+0），仅按生长维度计算会导致结果错误。

六、文档精准定位（立刻查找原文验证）

知识点	文档编号+章节	具体页码	关键原文内容
Avrami方程定义与公式	文档4（CAPE2710 Week7.pdf）Week7 Task1	e-book page162	“the Johnson-Mehl-Avrami equation: $f=1-exp(-k t^n)$; n=4 for 3D growth (spheres), n=3 for 2D growth (discs or plates), n=2 for 1D growth (rods or needles)”
Avrami指数与形核类型的关系	文档4 Week7 Task1	e-book page163	“Sporadic nucleation (nucleation throughout transformation) contributes an additional 1 to n; Instantaneous nucleation (all nuclei form at the start) contributes 0”
2D生长（盘状）的Avrami指数	文档4 Week7 Task1	e-book page163（表格）	“Disc + Sporadic → Avrami Exponent=3”
随机形核的宏观特征	文档4 Week7 Task1	e-book page161	“Sporadic nucleation leads to a range of particle sizes (early nuclei grow longer)”