
Double Integrals
1. Introduction
- 单变量积分(single-variable integral)表示曲线下的面积(曲线$f(x)$在$x=a$到$x=b$之间的面积):
$$\int_{a}^{b} f(x) dx$$ - 二重积分(double integral)表示曲面下的体积(曲面 $z=f (x,y) $ 与 $xy$ 平面之间、指定区域 $S$ 内的有符号体积):
$$\iint f(x, y) dxdy \quad \text{或} \quad \iint_S f(x, y) dS$$
其中 ( S ) 是 xy 平面上的区域,( dS ) 是面积微元(infinitesimal area element)
$f (x,y) dxdy$ 表示体积的无穷小柱体(infinitesimal column),积分过程就是将所有微元柱体累加.
2. How it works
- 二重积分通过迭代积分(iterated integration)计算:
$$\iint f(x, y) dxdy = \int \left( \int f(x, y) dx \right) dy$$ - 若积分限为常数,顺序可交换;若积分限含变量,顺序重要。
3. Simple Example
例1: 计算 ( f(x, y) = 1 ) 在区域 ( $2 \leq x \leq 5, 1 \leq y \leq 3$ ) 上的积分:
$$\int_{y=1}^{3} \int_{x=2}^{5} 1 dx dy = \int_{1}^{3} [x]_{2}^{5} dy = \int{1}^{3} 3 dy = [3y]_{1}^{3} = 6$$
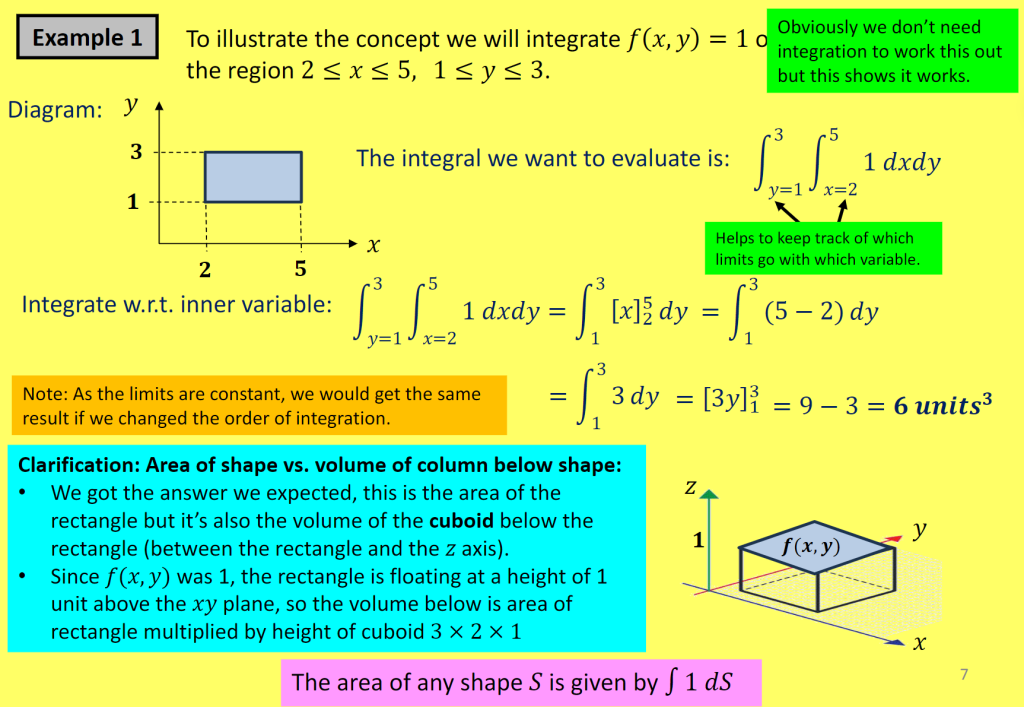
计算步骤:先积内层($x$ 方向):$\int_{x=2}^{5} 1 \, dx = x \big|_{2}^{5} = 5-2=3$;
再积外层($y$ 方向):$\int_{y=1}^{3} 3 \, dy = 3y \big|_{1}^{3} = 3×(3-1)=6$;
物理意义:结果既是矩形区域的面积($3×2=6$),也是 “高为 1 的长方体体积(面积 × 高 = 6×1=6)”
结论:常数限下,交换积分顺序结果不变(如先积 $y$ 再积 $x$,结果仍为 6)
结果表示矩形面积,也等于高为1的立方体体积.
4. Example: Constant Limits
例2a: 计算平面 ( $z = 1 + x + y$ ) 在矩形区域 ( $ 0 \leq x \leq 2, 0 \leq y \leq 1 $ ) 下的体积:
$$\int_{y=0}^{1} \int_{x=0}^{2} (1 + x + y) dx dy = \int_{0}^{1} \left[ x + \frac{x^2}{2} + yx \right]{0}^{2} dy = \int{0}^{1} (4 + 2y) dy = [4y + y^2]_{0}^{1} = 5$$
5. Example: Variable Limits
例3a: 计算 ( \iint_S x^2 y dS ),其中 ( S ) 是三角形区域(顶点为 (0,0), (1,0), (1,1)):
$$\int_{x=0}^{1} \int_{y=0}^{x} x^2 y dy dx = \int_{0}^{1} \left[ \frac{x^2 y^2}{2} \right]{0}^{x} dx = \int{0}^{1} \frac{x^4}{2} dx = \left[ \frac{x^5}{10} \right]_{0}^{1} = \frac{1}{10}$$
出处:L10 – Multiple Integration.pdf 第11页
6. Changing Order
例4: 计算:
$$\int_{0}^{1} \int_{y}^{1} 6y e^{x^3} dx dy$$
若先对 ( x ) 积分无法直接计算,改变顺序为:
$$\int_{x=0}^{1} \int_{y=0}^{x} 6y e^{x^3} dy dx = \int_{0}^{1} [3y^2]{0}^{x} e^{x^3} dx = \int{0}^{1} 3x^2 e^{x^3} dx$$
令 ( u = x^3 ),得:
$$\int_{0}^{1} e^u du = e – 1$$
7. Polar Coordinates
Polar coordinates 是二元变量替换中最常用的类型,专门用于处理圆域、圆环域或含\(x^2+y^2\)的被积函数,是考试核心内容.

- 极坐标变换公式:
$$x = r \cos \theta, \quad y = r \sin \theta$$ - 面积微元变换:
$$dxdy = r dr d\theta$$
例: 计算单位圆盘上的积分:
$$\iint_D \frac{1}{\sqrt{x^2 + y^2}} dxdy = \int_0^{2\pi} \int_0^1 \frac{1}{r} \cdot r dr d\theta = \int_0^{2\pi} \int_0^1 1 dr d\theta = 2\pi$$
Triple Integrals (不考)
1. 基本概念与计算
- 三重积分用于计算三维区域的体积或函数在空间中的积分:
$$\iiint_V f(x, y, z) dx dy dz$$
例: 计算立方体体积:
$$\int_{z=-1}^1 \int_{y=-1}^1 \int_{x=-1}^1 1 dx dy dz = 8$$
出处:L10 – Multiple Integration.pdf 第47页
2. Cylindrical & Spherical Coordinates
Cylindrical Polar Coordinates
$$x = r \cos \theta, \quad y = r \sin \theta, \quad z = z$$
体积微元:
$$dV = r dr d\theta dz$$
Spherical Polar Coordinates
$$x = r \sin \theta \cos \phi, \quad y = r \sin \theta \sin \phi, \quad z = r \cos \theta$$
体积微元:
$$dV = r^2 \sin \theta dr d\theta d\phi$$
出处:L10 – Multiple Integration.pdf 第56–59页
Average Value
定义
- 单变量函数平均值:
$$f_{\text{ave}} = \frac{1}{b – a} \int_a^b f(x) dx$$ - 二变量函数平均值:
$$f_{\text{ave}} = \frac{1}{A_R} \iint_R f(x, y) dA$$
例: 计算 ( $f(x, y) = e^{x+2y}$ ) 在三角形区域上的平均值。
L10 – Multiple Integration.pdf 第42–44页
物理意义
若 $f (x,y)\geq 0$,則 $A_R × f_{ave} = \iint_R f(x,y) dA$,即 “以 $R$ 为底、高为 $f_{ave}$ 的长方体体积,等于曲面 $z=f (x,y)$ 下的体积”;
类比:将曲面的 “山峰” 削平,填入 “山谷”,最终得到高度为 $f_{ave}$ 的平面.
Average value 的物理意义
想象一条曲线 $y = f(x)$ 在区间 $[a,b]$ 上的高度,平均值就是找到一个恒定高度,使得这个高度下的矩形面积等于曲线下的面积,相当于把”起伏不定”的曲线”拉平”到一个固定高度.
对于一维情况下的Av,想象一条曲线 $y = f(x)$ 在区间 $[a,b]$ 上的高度,平均值就是找到一个恒定高度,使得这个高度下的矩形面积等于曲线下的面积,相当于把”起伏不定”的曲线”拉平”到一个固定高度
对于二维情况下的 Av,假设 $f(x,y)$ 表示 temperature distribution,则 Av为平均温度;若为 density distribution,则 Av为平均密度;若为 stress distribution,则为 Av平均应力;若为 concentration distribution,则 Av为平均浓度. 公式 $A_R\times f_{ave}=\iint_Rf(x,y)dA$,这表示 $\text{底面积}\times\text{平均高度}=\text{总体积}$.
Change of Variables & Jacobian
1. 二变量变换
$$dudv = \left| \frac{\partial(u, v)}{\partial(x, y)} \right| dxdy$$
2. 三变量变换(不考)
$$dudvdw = \left| \frac{\partial(u, v, w)}{\partial(x, y, z)} \right| dxdydz$$
出处:L10 – Multiple Integration.pdf 第29–30、55页
Interpreting Types of Integrals (不考)
- 线积分:用于计算质量、功等
- 面积积分:用于计算总质量、电荷分布、热量等
- 体积积分:用于计算物体质量、通量密度等
出处:L10 – Multiple Integration.pdf 第6、62–63页
如果你需要我继续讲解某个具体例题、诊断题(Diagnostic Question)或变换过程,请告诉我,我会逐一详细解释。
0 条评论