Gibbs Free Energy

• 相变平衡应用：两相平衡（如固 – 液、液 – 气平衡）时，相变的吉布斯自由能变化Δtrs​G=0（平衡状态dG=0）；结合G=H−TS，可得：Δtrs​G=Δtrs​H−Ttrs​Δtrs​S=0⟹Δtrs​S=Ttrs​Δtrs​H​其中，Δtrs​H为Enthalpy of Transition，Ttrs​为Transition Temperature

• Trouton’s Rule：多数有机液体的Entropy of Vaporization Δvap​S约为85 – 88 $\text{J}\cdot\text{K}^{-1}\cdot\text{mol}^{-1}$，可用于估算未知液体的Δvap​H

大多数 non-associative liquids，比如苯、汽油，分子间不形成氢键，变成气体时的混乱度变化（\(\Delta_{\text{vap}} S\)）几乎一样，大概在\(85 \sim 88 \, \text{J·mol}^{-1}·\text{K}^{-1}\)之间；因此只要知道液体的沸点，就能估算它变成气体需要的能量（汽化焓）

Gibbs free energy的differential form

Variation of $G$ with $T$

$$(\frac{\partial G}{\partial T}​)p​=−S$$

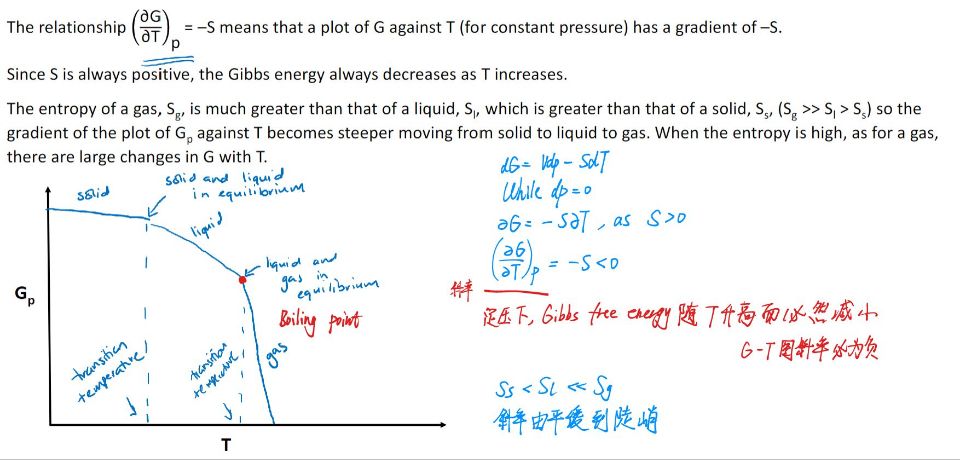
Variation of $G$ with $p$

$$(\frac{\partial G}{\partial p}​)T​=V$$

不同相态的Molar Gibbs Free Energy

以恒温的条件为前提，即：

$$(\frac{\partial G}{\partial p}​)T​=V$$

Condensed Phases：solid / liquid

condensed phases压缩性小，可假设体积\(V_m\)不随 $p$ 变化，积分得：$$G_m = G_m^\ominus + V_m \Delta p$$
其中$G_m^\ominus$为standard molar Gibbs free energy，\(p^\ominus=1\ \text{bar}\)），\(\Delta p = p – p^\ominus\)

Gas Phase

假设为ideal gas，\(V_m = RT/p\)，积分得：$$G_m = G_m^\ominus + RT \ln\left(\frac{p}{p^\ominus}\right)$$

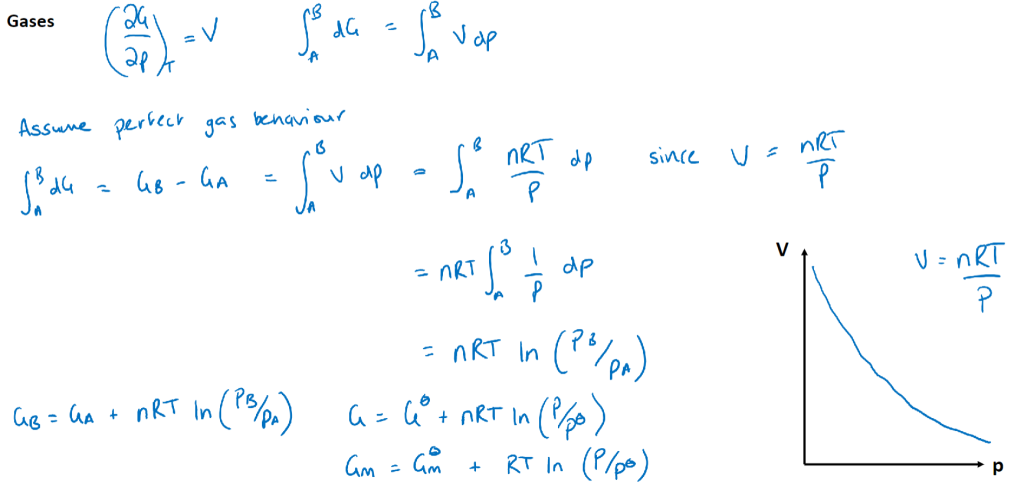
Phase transitions and equilibria

Definition

• Phase

物质中化学组成和物理状态均匀的部分.

• Vapour Pressure

condensed phase（固/液）与gas phase平衡时，气相产生的压强

气相压强在恒温下为定值

当vapour pressure等于外压时，液体开始沸腾，此时温度为boiling point $T_b$

• Phase Diagram $p-T$

以$p$为纵轴，$T$为横轴的图形，反应不同$p-T$条件下最稳定的相

Phase Rule

$$F=C-P+2$$

相律是为了计算$P$，其它量都会给出.

对于纯物质，Number of Components $C=1$

Number of Components是系统中Chemically Independent Species，即不能通过其它species的化学反应或浓度关系推导得到的species数量.

$$\boxed{C = S – R – R’}$$

• $S$：系统中所有物种的总数（如 “水 + 冰 + 水蒸气” 系统中，$S=1$，仅 $H_2O$）
• $R$：系统中 “独立的化学平衡反应数”（即不能由其他反应推导得到的化学反应）
• $R’$：系统中 “独立的浓度约束条件数”（如电荷平衡、浓度比例约束等）

示例：苯（A）+ 甲苯（B）的溶液 – 蒸气平衡

• 步骤 1：(S=2)（苯、甲苯，两相中物种相同）
• 步骤 2：无化学反应，(R=0)
• 步骤 3：无浓度约束（苯和甲苯比例可任意），$R’=0$

组分数 $C = 2 – 0 – 0 = 2$

相律 $F=2-P+2=4-P$，如单相时 F=3，可独立变 $ T$、$p$、浓度

相稳定性判断

$$G=H-TS$$

Gibbs Free Energy越小越稳定.

• 低温时：$TS$项影响小，Enthalpy占主导；固体 $G$ 最小，最稳定

• 高温时：$TS$项（负贡献）增大，Entropy主导；由于$S_{\text{固体}} < S_{\text{液体}} \ll S_{\text{气体}}$，气体 $G$ 最小，最稳定

• 高压时：$G=U+pV-TS$中，$pV$项主导，体积小（密度大）的相$pV$更小，$G $更低；例如：冰的$V_m$大于水（冰密度小），高压下水比冰稳定

Clapeyron Equation & Clausius-Clapeyron Equation

Proof of Clapeyron Equation

A, B两相平衡，则有$G_A=G_B$并且$dG_A=dG_B$；
由Gibbs Free Energy的differential表达式$dG=VdP-SdT$，代入得：

$$V_A dp – S_A dT = V_B dp – S_B dT$$

结合相变过程中熵的变化和体积的变化：

$$
\begin{cases}
&\Delta_{trs}S = S_B – S_A \\
&\Delta_{trs}V = V_B – V_A
\end{cases}
$$

最终得：

$$\frac{dp}{dT} = \frac{\Delta_{trs}S}{\Delta_{trs}V}$$

再结合相变平衡的$\Delta_{trs}S = \frac{\Delta_{trs}H}{T_{trs}}$，可改写为：

$$\frac{dp}{dT} = \frac{\Delta_{trs}H}{T_{trs}\Delta_{trs}V}$$

Properties of Clapeyron Equation

• 适用于所有类型的相变
• 物理含义：$\frac{dp}{dT}$是相边界的斜率，反映维持两相平衡时，$T$变化所需的$p$的变化率.

Clausius-Clapeyron Equation

推导（针对液 – 气相变）

对液 – 气相变（汽化），文档引入两个合理近似：

1. 液体体积远小于气体体积：\(V_{\text{液体}} \ll V_{\text{气体}} \implies \Delta_{vap}V \approx V_{\text{气体}}\)；
2. 气相近似为理想气体：\(V_{\text{气体}} = \frac{RT}{p}\)（摩尔体积）

把$\Delta_{\text{vap}} V_m \approx \frac{RT}{p}$和 Molar Enthalpy of Vaporization $\Delta_{\text{trs}} H_m = \Delta_{\text{vap}} H_m$代入克拉佩龙方程：

$$\frac{dp}{dT} = \frac{\Delta_{\text{vap}} H_m}{T \cdot \frac{RT}{p}}$$

整理后得到：

$$\frac{dp}{dT} = \frac{p \Delta_{vap}H_m}{RT^2}$$

积分形式

假设\(\Delta_{vap}H_m\)不随 T 变化，对\(\frac{dp}{p} = \frac{\Delta_{vap}H_m}{R} \cdot \frac{dT}{T^2}\)从\((T_A, p_A)\)到\((T_B, p_B)\)积分，得：

\(\ln\left( \frac{p_B}{p_A} \right) = -\frac{\Delta_{vap}H_m}{R} \left( \frac{1}{T_B} – \frac{1}{T_A} \right)\)

适用场景

• 仅适用于有气相参与的相变（液 – 气、固 – 气，即汽化、升华）
• 升华过程可类比，将\(\Delta_{vap}H_m\)替换为摩尔升华焓（Molar Enthalpy of Sublimation, \(\Delta_{sub}H_m\)），公式形式不变

Chemical Potential $\mu$

chemical potential可以理解为物质在系统中的 “逃逸倾向” 或 “转移能力”

物质从\(\mu\)高的区域自发向化学势\(\mu\)低的相或系统流动，直到各相 / 系统的化学势相等（达到平衡）

多相平衡时，同一组分在各相中的\(\mu\)相等，如冰 – 水平衡时$\mu_{冰} = \mu_{水}$

Single-Component System

单组分系统中，$G$ 与物质的量 $n$ 成正比（$G$ 是 Extensive property），定义Molar Gibbs Energy $G_m$为化学势：

$$\mu = G_m = \frac{G}{n}$$

对于single-component system，由于没有其它物质的影响，此时 $G$ 的微分式（含组成变化）为：

$$dG = Vdp – SdT + \mu dn$$

类比 Molar Volume

摩尔体积和化学势的定义，都是通过 “消除物质的量的影响”，将extensive property转化为intensive property

Multi-Component System

多组分系统有两种或更多物质（如盐水、空气），此时每个组分的化学势需考虑其他物质的影响，定义为偏摩尔吉布斯自由能.

partial molar Gibbs free energy

多组分系统（如 $A$、$B$ 混合物）中，$G$ 依赖 $p$、$T$ 及各组分的物质的量（$n_A, n_B,\cdots$），定义组分 $j$ 的化学势为：
$$\mu_j = \left( \frac{\partial G}{\partial n_j} \right)_{T, p, n_{i \neq j}}$$

$T, p, n_{i \neq j}$表示 “固定温度、压强，且其他组分的物质的量不变”；

物理意义

向系统中加入 1 mol 组分 $j$（其他条件不变）引起的 $G$ 变化，也称为Partial Molar Gibbs Energy.

Ideal Solution的chemical potential

理想溶液中，分子间作用力均匀，可通过 Mole Fraction \(x_i\) 描述浓度对化学势的影响：

• Solvent ，组分 A 的chemical potential

遵循Raoult’s Law：

$$\mu_A = \mu_A^* + RT \ln x_A$$

\(\mu_A^*\)：纯溶剂（\(x_A = 1\)）的chemical potential；\(x_A\)：溶剂的Mole fraction（\(0 < x_A < 1\)）；\(R = 8.314 \, \text{J·mol}^{-1}·\text{K}^{-1}\)；$T$：绝对温度（K）

• Solute，组分 B 的chemical potential

稀溶液中遵循Henry’s Law，有两种表达形式：

1. 以摩尔分数\(x_B\)表示：

$$\mu_B = \mu_B^\circ + RT \ln x_B$$

2. 以物质的量浓度\(c_B\)表示（\(c^\circ = 1 \, \text{mol·dm}^{-3}\)为标准浓度）：

$$\mu_B = \mu_B^{\circ, c} + RT \ln \frac{c_B}{c^\circ}$$

$mu_B^\circ$、$mu_B^{\circ, c}$为溶质的标准化学势，与浓度标度有关

系统类型	化学势公式	关键变量与说明
单组分系统	\(\mu = G_m\)	\(G_m\)：摩尔吉布斯自由能
	\(\left( \frac{\partial \mu}{\partial T} \right)_p = -S_m\)	\(S_m\)：摩尔熵；温度升高，化学势下降
	\(\left( \frac{\partial \mu}{\partial p} \right)_T = V_m\)	\(V_m\)：摩尔体积；压力升高，化学势上升
多组分理想溶剂	\(\mu_A = \mu_A^* + RT \ln x_A\)	\(\mu_A^*\)：纯溶剂化学势；\(x_A\)：溶剂摩尔分数
多组分理想溶质	\(\mu_B = \mu_B^\circ + RT \ln x_B\) 或 \(\mu_B = \mu_B^{\circ, c} + RT \ln \frac{c_B}{c^\circ}\)	\(x_B\)：溶质摩尔分数；\(c_B\)：溶质浓度；\(c^\circ = 1 \, \text{mol·dm}^{-3}\)
实际溶液	\(\mu_i = \mu_i^\circ + RT \ln a_i\)（\(a_i = \gamma_i x_i\)）	\(a_i\)：活度；\(\gamma_i\)：活度系数（\(\gamma_i = 1\)为理想）

在纯物质方程$dG = Vdp – SdT$基础上，加入组成变化的贡献：$dG = Vdp – SdT + \sum_j \mu_j dn_j$；

推广到其他热力学势（$U$,$ H$, $A$）：

$$dU = TdS – pdV + \sum_j \mu_j dn_j$$

$$dH = TdS + Vdp + \sum_j \mu_j dn_j$$

$$dA = -pdV – SdT + \sum_j \mu_j dn_j$$

不同势的化学势定义等价，仅偏导条件不同，考试重点为 $dG$ 的形式.

类比：电动势

离子化学势：\(\mu_j = \mu_j^\ominus + RT \ln a_j\)

电化学核心关系：\(\Delta G = -nFE\)

可以把 “电化学中的化学势” 理解为化学势在‘有电子转移的系统’中的应用；本质逻辑没变，只是多了 “电子” 这个参与物质，物质（包括离子、电子）都随化学势流动

Gibbs-duhelme equation

Appendix

考试易错点总结

混淆凝聚相与气相的 Gm 表达式

• 错误：用气相公式\(G_m = G_m^\ominus + RT \ln(p/p^\ominus)\)计算液体或固体的 G 变化；
• 正确：凝聚相用\(G_m = G_m^\ominus + V_m \Delta p\)（\(V_m\)小，\(\Delta G_m\)通常很小），气相用理想气体公式（\(\Delta G_m\)随 p 变化显著）。

相律中组分数$C$判断错误

• 错误：将混合物的 “物种数” 当作组分数（如 NaCl 水溶液，物种数为 3（NaCl、Na⁺、Cl⁻），但 C=2—— 物种数 – 1 个电离反应 = 3-1=2）；
• 正确：\(C = \text{物种数} – \text{独立化学反应数} – \text{浓度约束数}\)（纯物质\(C=1\)，无反应和约束）。

Clapeyron与Clausius-Clapeyron的适用场景混淆

• 错误：用克劳修斯 – 克拉佩龙方程计算固 – 液相变（如冰 – 水平衡）；
• 正确：
  • 克拉佩龙方程：适用于所有相变（固 – 固、固 – 液、液 – 气）；
  • 克劳修斯 – 克拉佩龙方程：仅适用于有气相的相变（液 – 气、固 – 气），且需满足\(V_{\text{凝聚相}} \ll V_{\text{气相}}\)。

化学势定义条件遗漏

• 错误：将\(\mu_j\)写成\(\left( \frac{\partial G}{\partial n_j} \right)_T\)（忘记固定 p 和\(n_{i \neq j}\)）；
• 正确：\(\mu_j = \left( \frac{\partial G}{\partial n_j} \right)_{T, p, n_{i \neq j}}\)—— 必须固定温度、压强和其他组分的物质的量，否则无物理意义

理想气体混合时误用总压代替分压

• 错误：计算\(G_{\text{最终}}\)时用总压 p 代替分压\(p_j\)（如\(G_{\text{最终}} = n_A (\mu_A^\ominus + RT \ln(p/p^\ominus)) + n_B (\mu_B^\ominus + RT \ln(p/p^\ominus))\)）；
• 正确：混合物中各组分的化学势由分压决定，\(p_j = x_j p\)，需代入\(p_j\)计算（如\(\ln(p_A/p^\ominus) = \ln(x_A p/p^\ominus)\)）

混合熵（\(\Delta_{mix}S\)）的符号错误

• 错误：认为\(\Delta_{mix}S < 0\)（误判\(\ln x_j\)的符号）；
• 正确：\(x_j < 1\)，\(\ln x_j < 0\)，故\(\Delta_{mix}S = -nR \sum x_j \ln x_j > 0\)（熵增，符合自发过程的熵增原理）