纯液体、理想溶液和非理想溶液

Chmical Potential of Pure Liquids

pure liquids与其自身vapour达平衡时，两者的chemical potential相等.

Input：pure liquid与vapour处于equilibrium

Algorithm：平衡时纯液体的化学势等于其蒸汽的化学势 $\mu^*(l) = \mu^*(g)$
将vapour pressure of pure liquid标记为 $p^*$，代入蒸汽相化学势公式；
替换分压 $p$ 为 $p^*$，得到纯液体化学势；

根据热力学基本方程，等温（\(dT=0\)）下\(dG_m = V_m dp\)，其中\(V_m\)为理想气体的摩尔体积，由理想气体状态方程\(V_m = \frac{RT}{p}\)代入，得：\(d\mu(g) = \frac{RT}{p} dp\)

积分结果为：\(\int_{\mu^\ominus(g)}^{\mu^*(g)} d\mu(g) = RT \int_{p^\ominus}^{p^*} \frac{dp}{p}\)

Output：$$\mu^*(l) = \mu^\ominus(g) + RT\ln\left(\frac{p^*}{p^\ominus}\right)$$
其中：\(\mu^*(l)\)（pure liquid chemical potential）、\(\mu^\ominus(g)\)（standard chemical potential of vapour，蒸汽相标准化学势）、\(p^*\)（vapour pressure of pure liquid）、\(p^\ominus\)（standard pressure，通常为 1 bar）；\(RT \ln\left(\frac{p^*}{p^\ominus}\right)\)：“偏离标准状态” 的修正项，反映蒸汽压\(p^*\)与标准压\(p^\ominus\)的差异对化学势的影响.

这种处理，利用相平衡将难以直接测量的纯液体化学势 \(\mu^*(l)\) 转化为可通过蒸汽压计算的蒸汽相化学势 \(\mu^*(g)\).

Ideal Solutions

intermolecular interactions

Raoult’s Law

Ideal Solutions中，某组分的蒸气压$p_A$等于其纯态蒸气压$p_A^{*}$与溶液中摩尔分数$x_A$的乘积：

$$p_A = x_A p_A^*$$

组分 A 的摩尔分数$x_{A}$是组分 A 的物质的量$n_{A}$ 与混合物总物质的量$n_{A}+n_{B}$ 的比值，namely：$$x_{A}=\frac{n_{A}}{n_{A}+n_{B}}$$

同时满足$x_{A}+x_{B}=1$.

所有组分的摩尔分数之和为 1，某一组分的摩尔分数变化必然伴随其他组分的反向变化；因此，Raoult’s Law反映了Ideal Solutions中组分蒸气压随组成的变化，加入溶质B使$x_A$减小，则$p_A$降低.

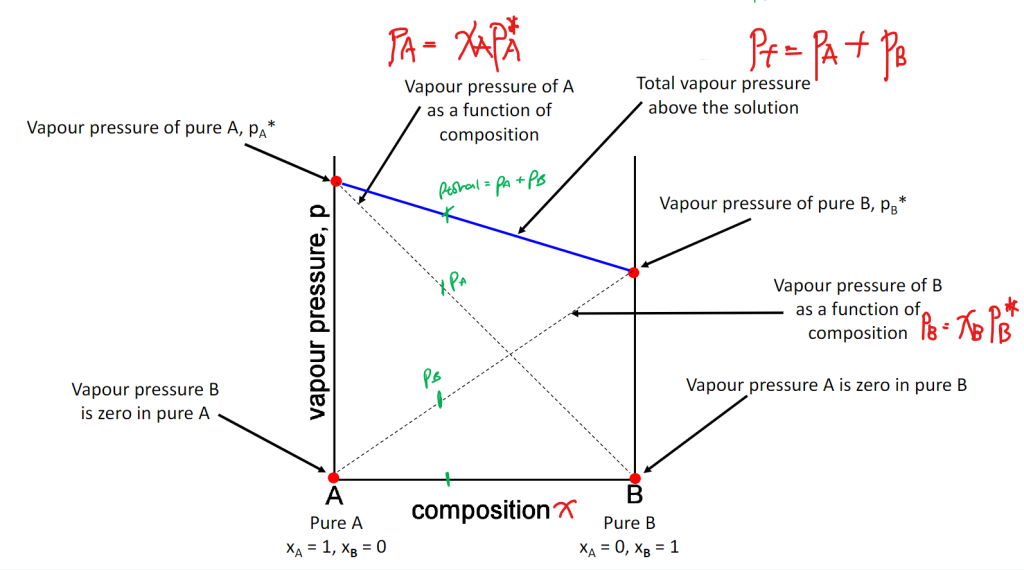
液相分子向气相的蒸发倾向被削弱；要么是难挥发溶质的 “物理阻碍 + 浓度稀释”，要么是非理想溶液中 “分子间强相互作用的束缚”，最终导致气相中分子数减少，蒸气压降低，也就是蓝线呈现出来的下降趋势.

Non-ideal Solutions

Deviation

非理想溶液中A-B相互作用与A-A, B-B差异显著，导致蒸气压偏离Raoult’s Law的预测：

• Positive Deviation

A-B 作用 < A-A/B-B 作用，分子易逸出，$p_A > x_A p_A^*$

如丙醇-水

• Negative Deviation

A-B 作用 > A-A/B-B 作用，分子难逸出，$p_A < x_A p_A^*$

如三氯甲烷 – 乙醚，形成氢键

Tips

溶质少，即$x_A$大，导致 $p_A$大：这是拉乌尔定律的正常现象，不是偏差；
溶质$x_A$ 固定，但$p_A$比$x_A p_A^*$大：这才是正偏差，根源是分子间作用变弱

Activity and Activity Coefficient

为将理想溶液化学势公式推广到非理想溶液，引入activity, $a_A$, 修正摩尔分数：

$$a_A = \gamma_A x_A$$

其中$\gamma_A$为activity coefficient，反映非理想程度：

• 理想溶液: $\gamma_A = 1$，$a_A = x_A$；
• 正偏差：$\gamma_A > 1$；
• 负偏差：$\gamma_A < 1$

非理想溶液组分化学势公式：

$$\mu_A(l) = \mu_A^{(l)} + RT\ln a_A = \mu_A^{(l)} + RT\ln(\gamma_A x_A)$$

Ideal Solubility & Thermodynamics of Mixing Ideal Solutions

Ideal Solubility

溶质化学势

理想溶解度指纯固体solute与溶液中溶质达平衡时的溶解度（饱和溶解度），此时纯固体化学势等于溶液中溶质化学势：

$$\mu_B^*(s) = \mu_B(sol)$$

其中$\mu_B^*(s)$为纯固体 B 的化学势

理想溶解度计算公式

结合理想溶液溶质化学势公式$mu_B(sol) = \mu_B^*(l) + RT\ln x_B$，代入平衡判据得：

$$\mu_B^(s) = \mu_B^(l) + RT\ln x_B$$

整理得：

$$\ln x_B = -\frac{\Delta_{fus} G}{RT}$$

其中$\Delta_{fus} G = \mu_B^{(l)} – \mu_B^{(s)}$为固体 B 的Gibbs energy of fusion.

Colligative Properties

Colligative Properties：仅依赖溶液中粒子相对数量，与粒子种类无关的性质，包括：lowering of vapour pressure, elevation of boiling point, depression of freezing point, osmotic pressure.

Elevation of Boiling Point

Depression of Freezing Point

纯物质的Melting Point (T_m)）是 solid 和 liquid 的 Chemical Potential (\mu)）相等的温度；当溶液中加入solute后，liquidoid（溶液）的化学势降低（Solute particles增加了体系的entropy，使gibbs free energy降低），但solidoid（Solid of pure solvent）的化学势不变

此时，只有降低温度，才能让固相的化学势也降低到与溶液的化学势相等，因此溶液的熔点 $T_{m,\text{sol}}$ 比纯溶剂的熔点 $(T_{m,\text{pure}}$ 低

熔点降低的程度可用以下公式定量描述：$$\Delta T_m = T_{m,\text{pure}} – T_{m,\text{sol}} = K_f \cdot b$$

其中：

• $\Delta T_m$：熔点降低值（纯溶剂与溶液的熔点差）
• (K_f)：Freezing Point Depression Constant，仅与溶剂的性质有关（如溶剂的摩尔凝固焓、摩尔质量等）
• $b$：溶质的质量Molality，定义为 “溶质的物质的量与溶剂的质量（kg）之比”

Osmotic Pressure