Classifying Crystal Structures
The Seven Crystal System
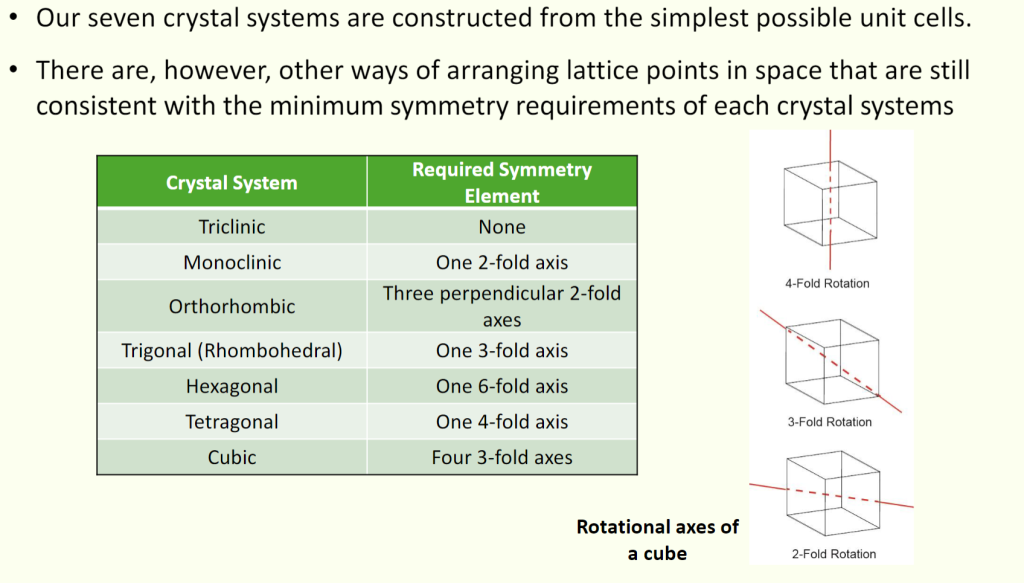
- Only SEVEN crystal system
There are only seven 3D unit cell shapes that can be packed together to be completely space-filling.
| Crystal System | Cell Parameters |
|---|---|
| Triclinic | $a \ne b \ne c$ ; $\alpha \ne \beta \ne \gamma \ne 90^{\circ}$ |
| Monoclinic | $a \ne b \ne c$ ; $\alpha = \gamma = 90^{\circ}, \beta \ne 90^{\circ}$ |
| Orthorhombic | $a \ne b \ne c$ ; $\alpha = \beta = \gamma = 90^{\circ}$ |
| Hexagonal | $a = b ≠ c$ ; $\alpha = \beta = 90^{\circ}$, $\gamma = 120^{\circ}$ |
| Trigonal (also called Rhombohedral) | $a = b = c$ ; $\alpha = \beta = \gamma ≠ 90^{\circ}$ |

Bravais Lattices
一定要理解这部分各个晶格的对称性问题
这个问题预计在这篇文章中详细阐述:http://www.adso2004.top/index.php/2025/10/20/symmetry-of-crystal-systems/
When combining 4 unit cell types with 7 crystal systems, we get only 14 unique Bravais lattices (not 4×7=28).
Why? Some combinations break the system’s symmetry, or result in the same lattice.
Representing Crystal Structures
- Clinographic view (斜视图): A 3D view to show the unit cell and atom positions.
- Plan view (平面图): A 2D view (looking down from one axis) to show atom positions in a layer.
- Coordination number (配位数): The number of adjacent atoms touching a central atom. For close-packed structures, it’s usually 12.
- Linking Polyhedra (多面体连接): Show how atoms form polyhedra (e.g., tetrahedra, octahedra) and how these polyhedra connect (e.g., ZnS structure links tetrahedra).
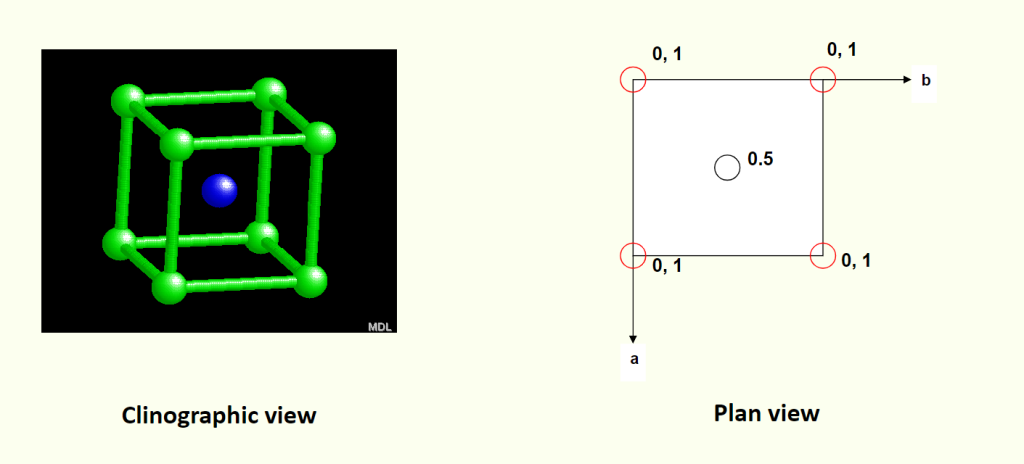
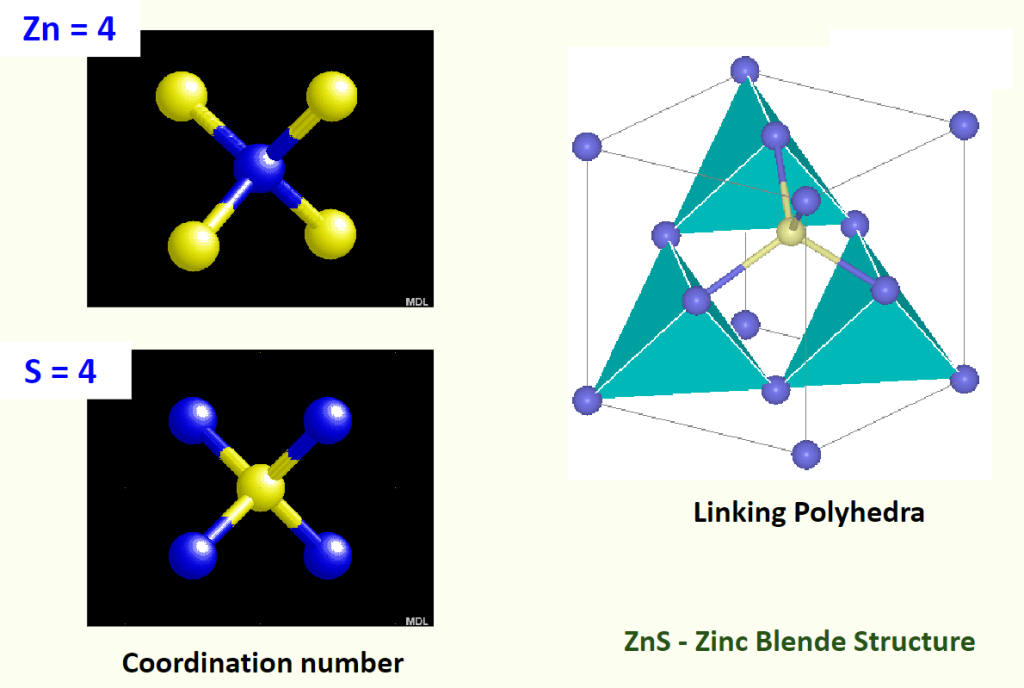
Assigning Coordinates to Atoms
Close-Packed Structures
Basic Concept
- 2D close packing
- 3D close packing
HCP Unit Cell
- Layer stacking order: ABABAB…
- Atom count in unit cell: 2
- Coordination number: 12
FCC Unit Cell
- Layer stacking order: ABCABC…
- Atom count in unit cell: 4
- Coordination number: 12
Other Cubic Cells
- Body-Centered Cubic
Found in alkali metals (e.g., Li, Na) and some transition metals.
It has 2 atoms per unit cell (8×1/8 + 1 = 2), coordination number = 8 (less tight than FCC/HCP)
- Simple Cubic
Only found in α-Polonium (α-Po).
It has 1 atom per unit cell (8×1/8 = 1), coordination number = 6 (very loose).
Packing Efficiency of FCC Unit Cell
$\text{Packing efficiency} = \frac{\text{Volume of atoms in unit cell}}{\text{Volume of unit cell}}$
0 条评论