Binomial Theorem

The binomial theorem expands expressions like $(a+bx)^n$ into a power series, there are two main cases:

$n$ is a positive integer

$n$ is a negative or fractional

形如$(a+bx)^n$的Binomial Power Series的指数$n$为negative或fractional时，该级数会成为infinite series，此时必须满足特定的收敛条件 —— 即存在Radius of Convergence，级数仅在收敛半径范围内收敛.

Maclaurin Series

Defination

Maclaurin series is a special power series, it expands a function $f(x)$ around $x=0$. To use it, the function must be differentialble many times.

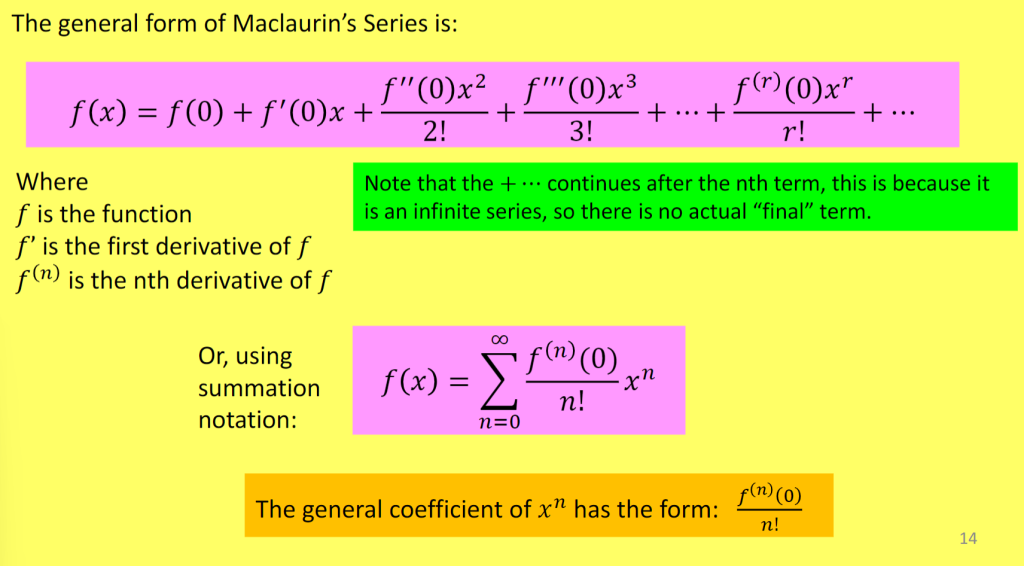
The general formula is:

$$f(x) = f(0) + f'(0)x + \frac{f”(0)x^2}{2!} + \frac{f”'(0)x^3}{3!} + \cdots + \frac{f^{(r)}(0)x^r}{r!} + \cdots$$

Tips: Taylor and Maclaurin

Taylor所有项围绕$(x-a)$的各次幂构建，依赖函数在$(x-a)$处的导数，核心有两种等价形式：

1. 展开 $f(x+a)$：$f(x+a) = f(a) + f'(a)x + \frac{f”(a)x^2}{2!} + \cdots + \frac{f^{(n)}(a)x^n}{n!} + \cdots$
2. 展开 $f(x)$：$f(x) = f(a) + f'(a)(x-a) + \frac{f”(a)(x-a)^2}{2!} + \cdots + \frac{f^{(n)}(a)(x-a)^n}{n!} + \cdots$

$a=0$时，即为Maclaurin series.

Common examples of Maclaurin series

Exponential function

All derivatives of $e^x$ are $e^x$, so $f(0) = f'(0) = f”(0) = 1$.

The series is: $e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \cdots$

Sine function

Derivatives of $\sin x$ cycle between $\cos x$, $-\sin x$, $-\cos x$, $\sin x$. At $x = 0$, only odd powers remain: $\sin x = x – \frac{x^3}{3!} + \frac{x^5}{5!} – \frac{x^7}{7!} + \cdots$

Big O Notation

When we truncate the Maclaurin series, there is an error. The Big notation describes the size of this error.

For example, if we write: $\sin x = x – \frac{x^3}{3!} + O(x^5)$

Here, $O(x^5)$ means: “The missing terms are all powers of $x$ equal to 5 or higher.”

麦克劳林级数的组合运算

Sum

将两个级数的同阶项相加 / 减，保留所需阶数：

示例：求 $\sin 2x – e^{-x}$ 到 $x^3$项的展开式

已知 $\sin 2x = 2x – \frac{(2x)^3}{3!} + \cdots = 2x – \frac{4x^3}{3}$ ；$e^{-x} = 1 – x + \frac{x^2}{2} – \frac{x^3}{6} + \cdots$

相减得：$\sin 2x – e^{-x} = (2x – \frac{4x^3}{3}) – (1 – x + \frac{x^2}{2} – \frac{x^3}{6}) = -1 + 3x – \frac{x^2}{2} – \frac{7x^3}{6} + \cdots$

Product

将两个级数相乘，仅保留所需阶数（高阶项乘积会超过目标阶，可忽略）。

示例：求 \(\ln(1-2x)\cos(3x)\) 到 \(x^3\) 项的展开式

已知 $\ln(1-2x) = -2x – 2x^2 – \frac{8x^3}{3} + \cdots$（收敛条件：$-\frac{1}{2} \leq x < \frac{1}{2}$）；

已知 $\cos(3x) = 1 – \frac{9x^2}{2} + \cdots$（收敛条件：所有 $x$）；

相乘得：$(-2x – 2x^2 – \frac{8x^3}{3})(1 – \frac{9x^2}{2}) = -2x – 2x^2 + \frac{19x^3}{3} + \cdots$；

收敛条件：取两者最严格的 $-\frac{1}{2} \leq x < \frac{1}{2}$

Taylor Series

这或许也应用了“从特殊到一般”的思想.

Maclaurin series only expands around $x=0$.

Taylor series is more general: it expands a function around any point $x=0$.

The general formula is: $$f(x) = f(a) + f'(a)(x – a) + \frac{f”(a)(x – a)^2}{2!} + \frac{f”'(a)(x – a)^3}{3!} + \cdots$$

Tips：$a$ in Taylor series

Taylor 级数的本质是将函数$f(x)$在某一特定点$x=a$附近展开为幂级数，这里的$a$就是“基准”.

Uses of Power Series

Calculate Limits

Taylor series本身围绕任意点$a$展开，但必须通过$t = x – a$，使$t \to 0$，从而使高阶项可忽略.

• 计算 $\lim_{x \to 0} \frac{\sin x}{x}$

问题：直接代入 $x=0$ 得 $\frac{0}{0}$（不定式）；

展开 $\sin x$：$\sin x = x – \frac{x^3}{3!} + \frac{x^5}{5!} + \cdots$；

代入极限：$\lim_{x \to 0} \frac{x – \frac{x^3}{3!} + \cdots}{x} = \lim_{x \to 0} \left(1 – \frac{x^2}{3!} + \cdots\right) = 1$

• 计算 $\lim_{x \to 1} \frac{3\ln x}{x^2 + 2x – 3}$

问题：直接代入 $x=1$ 得 $\frac{0}{0}$（不定式）；

展开 $\ln x$：令 $t = x – 1$（当 $x \to 1$ 时 $t \to 0$），则 $\ln x = \ln(1+t) = t – \frac{t^2}{2} + \frac{t^3}{3} + \cdots = (x-1) – \frac{(x-1)^2}{2} + \cdots$；

因式分解分母：$x^2 + 2x – 3 = (x+3)(x-1)$；

代入极限：$\lim_{x \to 1} \frac{3\left[(x-1) – \frac{(x-1)^2}{2} + \cdots\right]}{(x+3)(x-1)} = \lim_{x \to 1} \frac{3\left[1 – \frac{x-1}{2} + \cdots\right]}{x+3} = \frac{3}{4}$

Approximate Solutions to Equations

• 计算$\sin x = x – 0.1$的近似解（$x$接近 0）

展开$\sin x = x – \frac{x^3}{6} + O(x^5)$

代入方程：$x – \frac{x^3}{6} = x – 0.1 \Rightarrow x^3 = 0.6 \Rightarrow x \approx 0.843$

Solve Differential Equations

Radius of Convergence

这点不考.