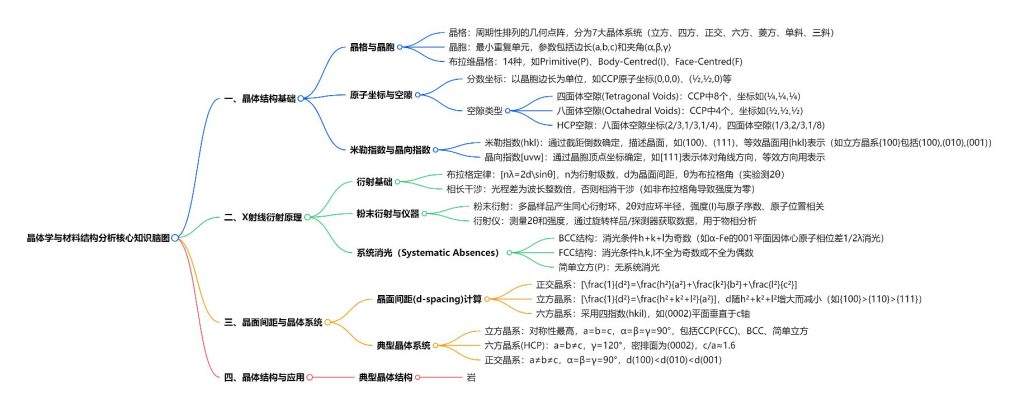
材科基这部分内容：

文档1：HCP空隙
文档2：六方晶胞与米勒指数
文档3：米勒指数与方向指数详解
文档2：晶体结构与分数坐标
文档3：米勒指数与晶面对称
文档4：晶体方向指数与离子晶体结构
文档5：晶面间距
L6：布拉格定律与X射线衍射基础
文档7：X射线衍射中的系统消光

Motifs

lattice (how to repeat)
motif (what to repeat)

$$\text{crystal}=\text{lattice}+\text{motif}$$

Plan Views

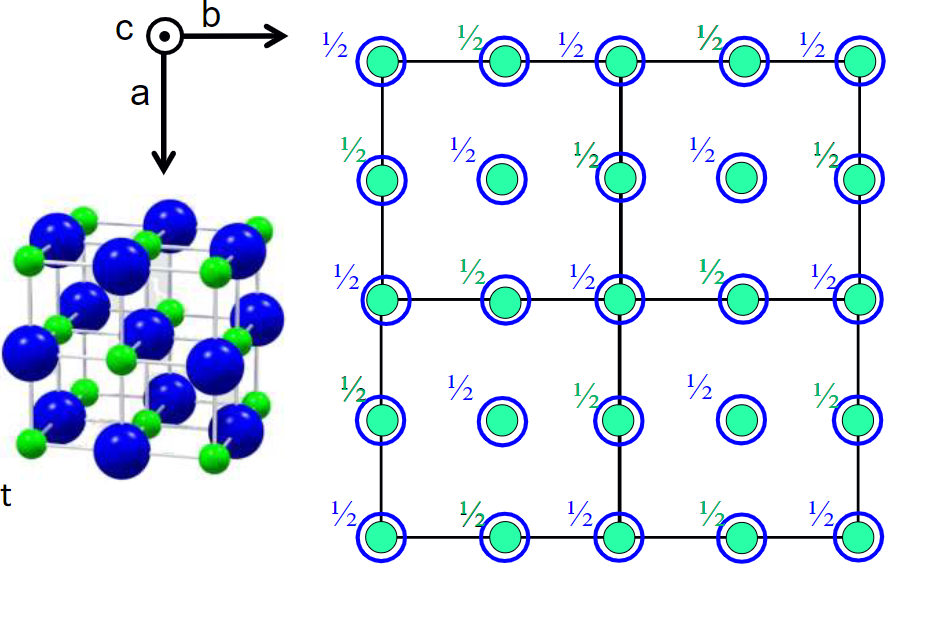
• “Standard” Lattice Plan Views

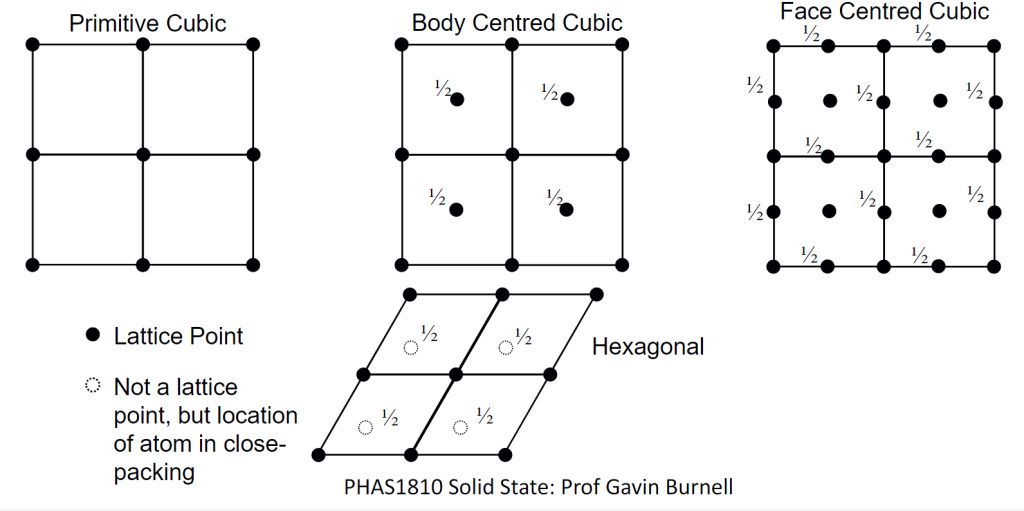
间隙原子的存在是附加特征，不改变主体晶格的类型；Lattice points的分布方式和对称性决定了其所属的 Bravais Lattices 类型.

• $\ce{CaF2}$

晶胞内有4个$\ce{Ca}$和8个$\ce{F}$，但化学式表示的是晶体中原子的最简整数比，而非晶胞内原子的绝对数目，因此化学式为$\ce{CaF2}$.

基矢

定义晶体坐标系，不一定是笛卡尔坐标系（夹角不一定为90°）

Planes in Lattices

Miller indices

http://www.adso2004.top/index.php/2025/04/14/miller-indices/

米勒指数是晶面截距倒数的最小整数比.

Interplanar Spacings (d-spacings)

Perpendicular distance between lattice planes

晶面间距由miller indices($hkl$)表征，与晶胞边长参数（$abc$）相关.

For orthogonal crystal system (all 90° angles)

$$\frac{1}{d^{2}} = \frac{h^{2}}{a^{2}} + \frac{k^{2}}{b^{2}} + \frac{l^{2}}{c^{2}}$$

For cubic crystal system: $ a = b = c $，$\frac{1}{d^2} = \frac{h^2 + k^2 + l^2}{a^2} $.

Sequence of planes of decreasing d-spacing

$h^2 + k^2 + l^2$的值越大，$\frac{1}{d^2}$ 越大，晶面间距 $d$ 越小l越大，$\frac{1}{d^2}$ 越大，晶面间距 $d$ 越小l

共面定律

$$Uh+Vk+Wl=0$$

Spatial Frequencies & Reciprocal Space

只要存在周期性，无论是时间上的循环（如四季更替、心跳）还是空间上的重复（如晶面排列、光栅条纹），都可以用频率来量化其重复的快慢程度.

• Wavenumber

https://www.youtube.com/watch?v=jGD6GyUP3uc

• 波数矢量的分量

波数矢量的分量由晶面的米勒指数（Miller Indices）\((hkl)\) 决定：

对于正交晶系（如立方晶系），波数矢量的模长满足： \[ |\underline{g}_{hkl}| = \frac{2\pi}{d_{hkl}} = \sqrt{\left( \frac{2\pi h}{a} \right)^2 + \left( \frac{2\pi k}{b} \right)^2 + \left( \frac{2\pi l}{c} \right)^2} \] 其中 \(a, b, c\) 为晶格参数

对于立方晶系（\(a = b = c\)），进一步简化为： \[ |\underline{g}_{hkl}| = \frac{2\pi}{a} \sqrt{h^2 + k^2 + l^2} \]

• 波数矢量的定义式

$$\underline{g}_{hkl} = \frac{2\pi}{d_{hkl}} \cdot \hat{n} $$

Wavenumber Vector\(\underline{g}\)）的模长 \(|\underline{g}| = \frac{2\pi}{d}\)，恰好是spatial frequency \(\frac{1}{d}\) 的 \(2\pi\) 倍，即 \(|\underline{g}| = 2\pi \times\) 空间频率

晶系、晶格

晶系类型（Crystal Systems）：房子的形状

根据房子的“长宽高（\(a,b,c\)）”和“墙角角度（\(\alpha,\beta,\gamma\)）”分类，共7种形状

布拉维晶格（Bravais Lattices）：房子里的家具摆放

在每种“房子形状（晶系）”里，原子（家具）可以放在不同位置，形成14种“摆放方式”

晶格类型：布拉维晶格的标签（P/I/F/C/R等）

布拉维晶格本质上是这些摆放方式的组合.

• 简单房（P）：原子只在房子的 8 个角落（顶点）
• 体心房（I）：角落 + 房子中心有原子（像房子中间有根柱子）
• 面心房（F）：角落 + 每个墙面中心有原子（像墙上挂装饰）
• 底心房（C）：角落 + 底面中心有原子（仅底面有装饰）

HCP

Voids

https://unacademy.com/content/neet-ug/study-material/chemistry/octahedral-voids/

Octahedral voids are voids enclosed by six spheres in octahedral configurations.

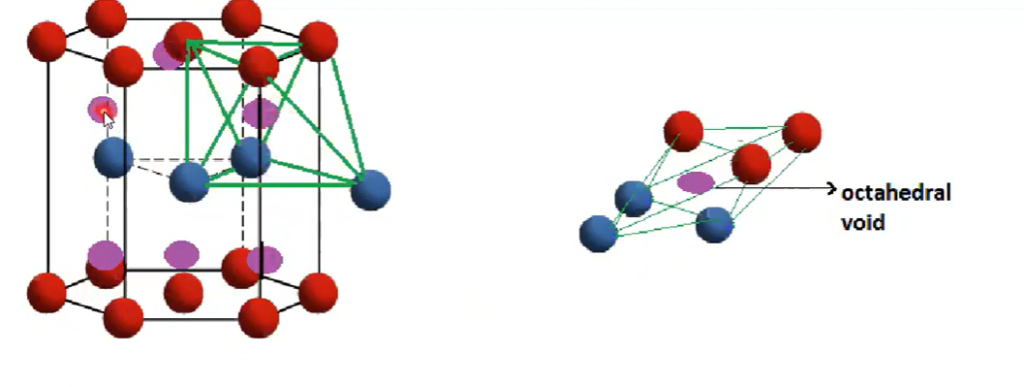
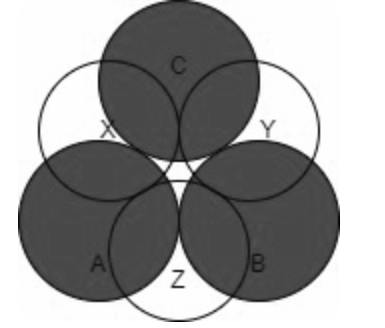
The number of octahedral voids is equal to n or half that of tetrahedral voids.

X-ray and Bragg’s law

Bragg’s law

\begin{aligned}
&AB+BC=n\lambda\\
&AB=BC=d\sin\theta\\
&\Rightarrow n\lambda=2d\sin\theta
\end{aligned}

X射线照射到晶体上时，晶体中大量原子会作为散射中心对X射线进行散射，这些散射波会相互干涉；干涉有两种结果，相长干涉和相消干涉，只有当干涉结果为前者，即波峰与波峰、波谷与波谷叠加时，散射波的振幅才会显著增大，从而形成可被探测到的衍射信号，因此有$AB+BC=n\lambda$.