U9

9.2 The Bonding in Organic Molecules

Hybridisation

• 杂化类型的判断方法

$$\text{杂化数} = \text{连接的原子数（和键数无关）}+ \text{孤对电子数}$$

$$\text{含双键就是} sp^2 \text{杂化},\text{含三键就是} sp \text{杂化}$$

杂化数（即杂化类型）决定了空间构型.

所谓双键、三键，之所以被称为“不饱和键”，就是因为它们是由未参与杂化的p轨道形成的.

HOMO and LOMO orbitals

并非独立于成键轨道、反键轨道之外的 “特殊分子轨道类型”，而是对分子轨道电子填充状态的一种描述. 它们反映了成键轨道和反键轨道在电子填充中扮演了怎样的角色.

9.3 Functional groups and oxidation level

• 基本官能团
• Oxidation and Reduction

氧化反应：得氧失氢、失电子
还原反应：失氢得氧、得电子

Inductive properties

诱导效应是电负性原子极化分子中 σ 键（σ – bonds）的方式

基本方式就是比较基团的电负性.

• 具有$-I$ electron-withdrawing effects的基团

Strong：$\ce{X-(X=F,Cl,Br,I)}$，$\ce{-O}$，$\ce{NH3}$

Weak：$\ce{OH-}$，$\ce{NH2-}$

• 具有$+I$ electron-donat ing effects的基团

$\ce{CH3+}$，$\ce{Li+}$，$\ce{MgBr+}$

Resonance

轨道离域（Orbital delocalisation）使 π 键电子（π -bonding electrons）能够在分子中移动，而非局限于某两个原子之间

当分子存在共轭体系（如多个双键交替排列）时，π 轨道相互重叠，形成离域的大 π 轨道，电子不再定域于单个双键，而是在整个共轭区域内离域

Carbocation Stability

Mesomeric properties

https://byjus.com/jee/mesomeric-effect

中介效应源于通过共振共轭（resonance conjugation）在分子的 π 体系（π – system）内的电子密度移动（the movement of electron density）

The group which shows the $–M$ effect includes：

$\ce{–NO2, –CN, –COX, –SO3H, – CHO, –CONH2, –COR, –COOH, –COOR}$ etc.

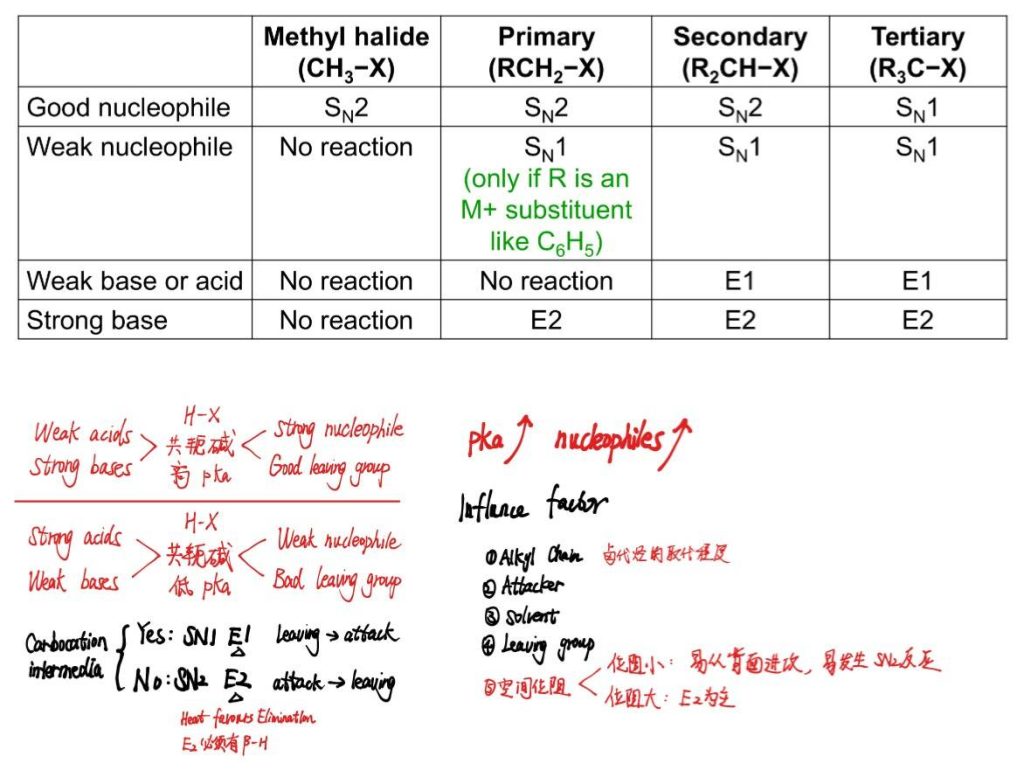
9.4 Nucleophilicity and Reaction Mechanisms

亲核反应机理：Nucleophile & Base

What Makes A Good Nucleophile?

U10 The Laws of Thermodynamics and Chemical Reactions

Basic

Extensive & Intensive Properties

• extensive：与amount相关
  质量、体积
• intensive：与amount无关
  温度、压力

$$\frac{\text{extensive properties}}{\text{amout}}=\text{intensive properties}$$

$$V_m=\frac{V}{n}$$

$2^{nd}$ Law of Thermodynamics

• Spontaneous processes

1. 热运动自发扩散不做功（Ideal mixing by diffusion）
2. 气体向真空膨胀不做功（Joule Gas Expansion）

仅靠吸放热，无法预测物理或化学变化过程是否自发，必须有第二个判据.

• Entropy Change of the Surroundings ($\Delta S_{surr}$)

热力学第二定律即是针对反应自发性的结论.

The size of the entropy change depends on the temperature: $$\Delta S_{\text{surr}}=\frac{-\Delta H}{T}$$

• $2^{nd}$ Law of Thermodynamics

In a spontaneous process the total entropy of the Universe increases.

$$\Delta S_{\text{sys}} + \Delta S_{\text{surr}} \geq 0$$

\begin{aligned}
\Delta S_{\text{sys}} – \frac{\Delta H}{T} &\geq 0\\
T\Delta S_{\text{sys}} – \Delta H &\geq 0\\
0 &\geq \Delta H – T\Delta S_{\text{sys}}
\end{aligned}

• $\Delta G$ and Spontaneity

Gibbs Free Energy, $\Delta G$, is the maximum work that can be obtained from a change without expansion of the system.

$$\Delta G = \Delta H – T\Delta S$$

$$\Delta G=-RT\ln K$$

1. $\Delta_r G<0$: The process is spontaneous.
2. $\Delta_r G=0$: The process is at equilibrium.
3. $\Delta_r G>0$: The reverse process is spontaneous.

A spontaneous process must have $\Delta G<0$ ,and $K>0$ (favouring products).

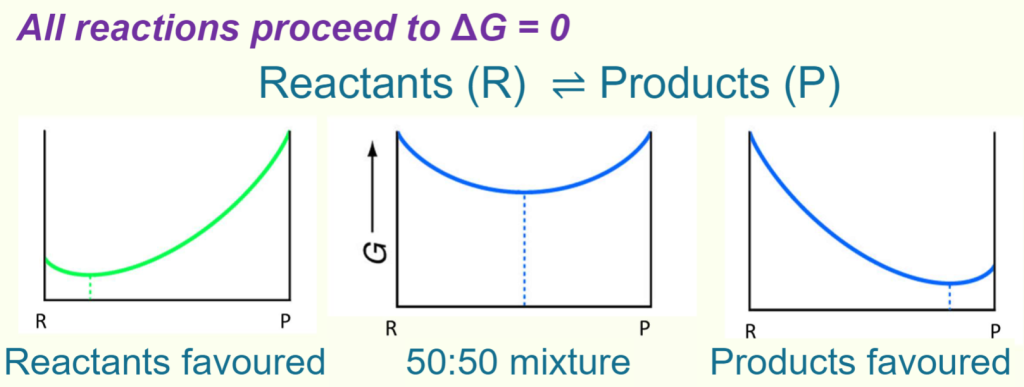
For an irreversible reaction, the equilibrium state is reached when all reactants are used up.

$Q$ – The Reaction Quotient

对于反应 $aA + bB \rightleftharpoons cC + dD$，其反应商 $Q_c$ 的表达式为：

$$Q_c = \frac{[C]^c [D]^d}{[A]^a [B]^b}$$

Gibbs Energy and Equilibria

$$G = G^\ominus + RT\ln Q$$

At equilibrium, $Q = K$

$\Delta G^\ominus = -RT\ln K$ and $\Delta G^\ominus = \Delta H^\ominus – T\Delta S^\ominus = 0$

$$\Delta H^\ominus – T\Delta S^\ominus = -RT\ln K$$

Heat, work and the First Law of Thermodynamics

The First Law of Thermodynamics

The First Law describes how the system interacts with the surroundings during a chemical change.

Internal Energy and Enthalpy

lecture10.2

• Work and Reversibility

在可逆过程中，系统能做 最大功（Maximum work）；这是因为该过程中，体积膨胀导致的内能损失（internal energy loss）被最小化

10.6 Redox Reactions and Electrochemistry

Redox Reactions and Ions in Solution

U11 Kinetics

$Chemistry^3$在小绿鲸中大概408页左右.

Fundamental

反应物与生成物反应速率呈镜像关系，在同一时刻，反应物消耗速率$-\frac{d|A|}{dt}$与产物生成速率$-\frac{d|P|}{dt}$数值相等，符号相反（same magnitude，opposite sign）

Rate Coefficients

反应速率常数$k$是反应的固有属性，不同反应$k$值也不同：

$$A \xrightarrow{k_1} P_1,B \xrightarrow{k_2} P_2$$

$$k_1\ne k_2$$

Enzyme Kinetics

Enzyme对substrate浓度$[S]$有复杂依赖，因底物结合和产物解离的平衡影响速率：
$$\text{E} + \text{S} \rightleftharpoons \text{ES} \rightarrow EP \rightarrow E+P$$

Elementary Reactions

• Unimolecular

单分子反应遵循一级反应动力学，即$-\frac{d|A |}{dt}\propto [A]$

由此推导出速率方程：

$$-\frac{d|A |}{dt}= k_{uni}[A]$$

对方程两边积分：
$$\int\frac{1}{|A |}d[A]=-\int k_{uni}dt$$
$$ln[A]t=-k_{uni}t+c$$

当$t=0$时，$c=ln[A]_0$，得到：

$$ln[A]_t=-k_{uni}t+ln{A}_0$$

Anti-log：

$$[A]t=[A]_0\exp(-k_{uni}t)$$

• Bimolecular

对于双分子反应$A+B\rightarrow P,-\frac{d|A |}{dt}\propto [A][B]$

由此推导出速率方程：

$$-\frac{d|A |}{dt}= k_{bi}[A][B]$$

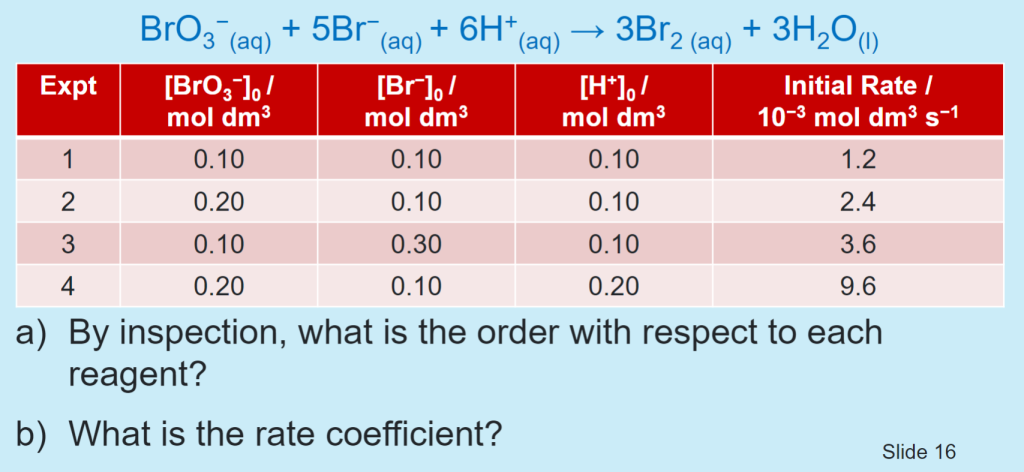
Measuring the Order of Reaction, and Parallel Reactions

Measuring the Order

当一种反应物大量过量时，可将原本的二级反应视作一级反应，这种情况称为 伪一级反应（pseudo – first – order reaction）

• Isolation Method

For the reaction: $aA + bB + cC \to P$

$$ \frac{-d[A]}{dt} = k[A]^a[B]^b[C]^c $$

If $[B]$ and $[C] \gg [A]$, the rate equation:

$$ \frac{-d[A]}{dt} = k[B]^b[C]^c $$

can be simplified by defining $k’ = k[B]^b[C]^c$, leading to:

$$ \frac{-d[A]}{dt} = k'[A]^a $$

This form is analogous to the simpler rate equations we encountered previously.

• Integral method

Solution

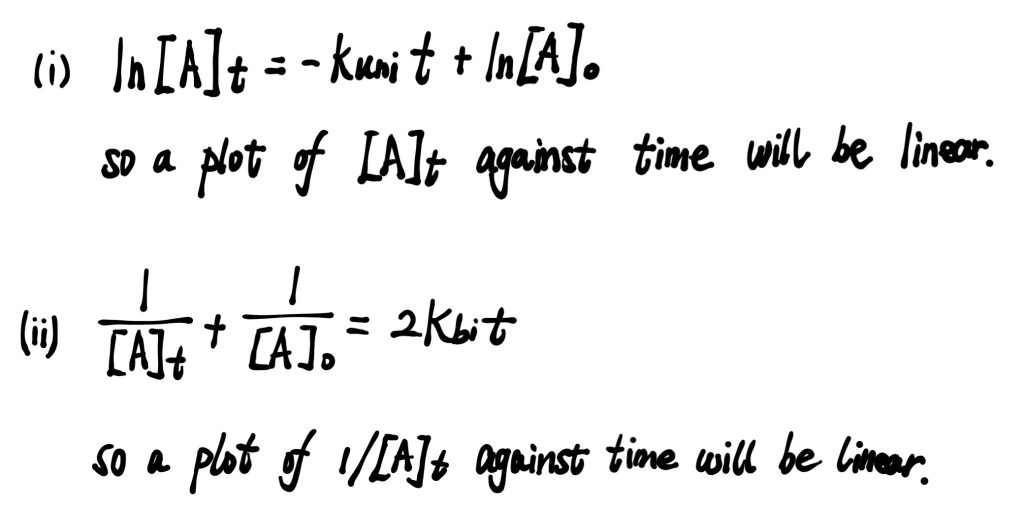
Where we determine the ‘shape’, or the relationship between $[A]$ and $t$.

1. If a graph of $\ln{[A]}_t$ against $t$ is a straight line, then $a = 1$.
2. If a graph of $\frac{1}{[A]_t}$ against $t$ is a straight line, then $a = 2$.

• Differential method

The differential of $[A]$ against $t$, is the gradient or rate.

We know that for elementary reactions: $\frac{d[A]}{dt} = k'[A]^a$, measuring gradients along one decay, and plot the gradients against $[A]$.

Or we take the initial gradient at $t = 0$, then repeat the experiment at different $[A]_0$ values.

11.3这部分，还需要复习一级反应和二级反应.

Solution

Transition Metal Chemistry

• 晶体场分裂

• 高低自旋

• 螯合效应

• CFAE 

Crystal Field Theory

过渡金属的性质无法用主族元素的价键理论来解释（如orbital hybridisation），而crystal field theory即是考虑ligands如何影响金属$d$轨道的能量.

自由金属离子的 5 个 $d$ 轨道$d_{xy}, d_{xz}, d_{yz}, d_{z²}, d_{x²-y²}$能量完全相同，称为五重简并；配体的存在打破对称性，通过静电排斥（负点电荷配体与 $d$ 电子的排斥）导致轨道能量分裂，简并度降低.

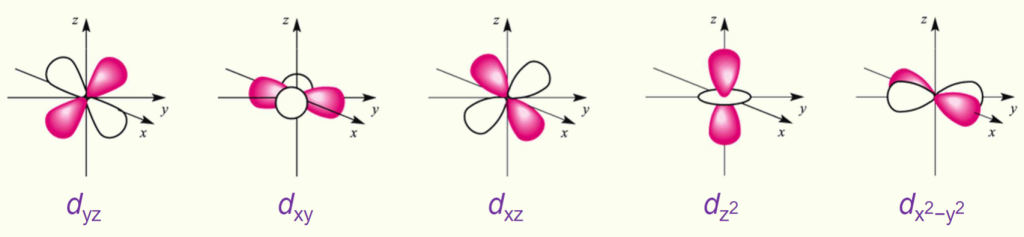
在晶体场理论中，将ligands视为negative point charges：

• 若配体是像$Cl^-$或$OH^-$这样的阴离子，其负电荷属性显而易见
• 若配体是像$H_2O$或$NH_3$这样的中性分子，负电荷则源于与孤对分子轨道（lone pair MO）相关的偶极（dipole）：以$NH_3$为例，氮原子上的孤对电子形成偶极，一端为$δ-$（负电端），一端为$δ+$（正电端）

Octahedral Complexes

6 个配体沿 (x, y, z) 轴的正负 6 个方向分布（位于正八面体的 6 个顶点），这样就导致了$d$轨道的分裂：

• $d_{z^2}) 和 (d_{x^2−y^2}$ 轨道的波瓣（lobes，轨道的空间伸展方向）直接指向负点电荷，它们与配体（ligands）的排斥力大，因此能量更高
• $d_{yz}$、$d_{xy}$ 和 $d_{xz}$轨道的波瓣指向配体之间的空隙，电子受配体排斥力较小，所以能量更低

由此可知，在octahedral environment中，过渡金属$d$轨道分裂成两组：

• 能量较低的三个轨道$t_{2g}$
• 能量较高的两个轨道$e_g$

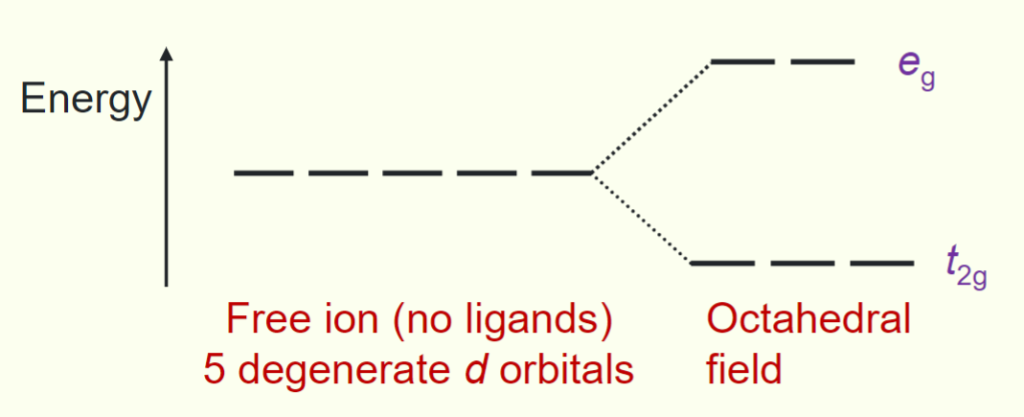
$\Delta_{oct}$ 表示晶体场分裂参数（crystal field splitting parameter）

• $t_{2g}$ 轨道的能量降低了 $-\frac{2}{5}\Delta_{oct}$（$t_{2g}$ orbitals are lowered in energy by $-\frac{2}{5}\Delta_{oct}$）；
• $e_g$ 轨道的能量升高了 $+\frac{3}{5}\Delta_{oct}$（$e_g$ orbitals are raised in energy by $+\frac{3}{5}\Delta_{oct}$）

从配合物形成时整体 $d$ 轨道的能量变化来看，
$(2 \times \frac{3}{5}\Delta_{oct}) – (3 \times \frac{2}{5}\Delta_{oct}) = 0$

这表明虽然 $d$ 轨道发生了分裂，但总体能量保持不变，符合能量守恒原理（The overall $d$-orbital energy change from complex formation is $(2 \times \frac{3}{5}\Delta_{oct}) – (3 \times \frac{2}{5}\Delta_{oct}) = 0$）

Tetrahedral Crystal Field

Square planar

$d$轨道与ligand（negative point charges）的空间位置关系，决定了配合物各条$d$轨道的能量差异.

• (d_{z^2}) 轨道：在与负电荷（配体，可视为负点电荷）相同的平面内有一个小的 轨道波瓣（orbital lobe），但轨道的大部分远离 点电荷（point charges），与负电荷的静电排斥作用较弱，因此能量略低（slightly lower in energy）
• (d_{xz}) 和 (d_{yz}) 轨道：离负电荷最远（furthest away from the negative charges），与负电荷的静电排斥作用最弱，因此具有 最低的能量（lowest energy），且二者是简并的（degenerate），即能量相同

Electron Configurations

The Spectrochemical Series and the Jahn-Teller Effect

晶体场理论回顾（Recap – Crystal Field Theory）

晶体场理论（Crystal Field Theory, CFT）指出，过渡金属的d轨道能量会被配体（ligands）形成的负电荷场分裂，分裂方式取决于配体的几何构型（如八面体、四面体、平面正方形）及配体与d轨道的静电排斥作用。例如：

• 八面体场（Octahedral）：d轨道分裂为能量较高的e_g轨道（d_{x²−y²}, d_{z²}）和能量较低的t_{2g}轨道（d_{xy}, d_{xz}, d_{yz}），分裂能记为Δ_oct。
• 四面体场（Tetrahedral）：分裂能Δ_tet约为Δ_oct的4/9，t₂轨道能量高于e轨道。
• 平面正方形场（Square planar）：分裂能Δsp最大，d{x²−y²}轨道能量最高。

晶体场稳定能（Crystal Field Stabilisation Energy, CFSE）影响过渡金属配合物的结构、磁性、颜色和反应动力学。当分裂能Δ大于电子成对能（spin pairing energy, P）时，形成低自旋（Low spin, LS）配合物；反之形成高自旋（High spin, HS）配合物。

分裂能（Δ）的影响因素（Factors Controlling the Size of Δ）

1. 金属氧化态（Metal oxidation state）
   金属离子电荷越高，对配体的吸引力越强，Δ越大。例如：

• [Fe(H₂O)₆]²⁺的Δ_oct为9400 cm⁻¹，
• [Fe(H₂O)₆]³⁺的Δ_oct为13700 cm⁻¹。
  高价态金属（如M(III)）更易形成低自旋配合物。

1. 过渡金属周期（Transition series of metal）
   同一族中，第二、三过渡系金属的Δ大于第一过渡系（如Rh³⁺ > Co³⁺），因其d轨道扩展，电子成对能P较低，故第二、三过渡系配合物通常为低自旋。
2. 同周期金属差异（Identity of the metal across a row）
   同配体、同氧化态时，第一过渡系金属的Δ变化不规律，例如：

• [Ti(H₂O)₆]³⁺的Δ_oct为20300 cm⁻¹，
• [Fe(H₂O)₆]³⁺的Δ_oct为13700 cm⁻¹。

1. 配合物几何构型（Geometry of the complex）

• 平面正方形（Square planar）Δ_sp最大，
• 八面体（Octahedral）Δ_oct居中，
• 四面体（Tetrahedral）Δ_tet最小（Δ_tet = 4/9 Δ_oct）。

1. 配体类型（Identity of the ligand）
   配体按分裂能从小到大排列形成光谱化学序列（Spectrochemical Series）：
   [
   I^{-} < Br^{-} < Cl^{-} < F^{-} < H_{2}O < NH_{3} < en < bpy < phen < PR_{3} < CO \approx CN^{-}
   ]
   弱场配体（Weak field ligands，如卤素离子）产生小Δ，强场配体（Strong field ligands，如CO、CN⁻）产生大Δ。晶体场理论无法解释该序列（如中性配体CO为强场），需结合分子轨道理论（MO theory）

配合物几何构型的预测（Understanding and Predicting Geometries）

• 四面体配合物（Tetrahedral Complexes）
  弱场配体（如Cl⁻）、第一过渡系金属（如Ni²⁺, d⁸）或d⁷电子构型（如Co²⁺）倾向形成四面体，因Δ小，CFSE贡献低，如[NiCl₄]²⁻。
• 平面正方形配合物（Square Planar Complexes）
  d⁸电子构型（如Ni²⁺、Rh(I)）在强场配体（如CN⁻）或第二、三过渡系金属中易形成平面正方形，如[Ni(CN)₄]²⁻，此时CFSE最大且电子构型稳定（全满d轨道）。
• 八面体配合物（Octahedral Complexes）
  多数d区金属形成八面体，因CFSE高，如[Ni(H₂O)₆]²⁺（Ni²⁺, d⁸）

Jahn-Teller效应（Jahn-Teller Effects）

理论核心：简并量子态会发生畸变以消除简并性

• Cu²⁺配合物（d⁹, t_{2g}⁶e_g³）
  e_g轨道（d_{z²}, d_{x²−y²}）上的电子分布不均导致简并，引发结构畸变：
• 若d_{z²}轨道填充2个电子，d_{x²−y²}填充1个电子，配合物沿z轴拉长（elongation）；
• 反之沿z轴压缩（compression）
  畸变使两个电子进入低能轨道，一个进入高能轨道，整体能量降低
• 典例
  [CuCl₆]⁴⁻、[CuBr₆]⁴⁻等八面体配合物常出现轴向拉长畸变。
• 适用电子构型
  八面体中e_g轨道电子数为奇数的构型（如d⁴高自旋、d⁷低自旋、d⁹），四面体配合物中t₂轨道电子数不均的构型也可能发生Jahn-Teller畸变

关键结论（Lecture 12.4 Learning）

1. 分裂能Δ的影响因素：金属氧化态、过渡系周期、配体类型及几何构型
2. 光谱化学序列：实验确定的配体强弱顺序，强场配体导致大Δ，易形成低自旋配合物

3.几何构型与电子构型：

• d⁸金属离子（如Ni²⁺）在强场下呈平面正方形；
• 弱场或d⁷构型倾向四面体

1. Jahn-Teller效应：消除简并态的结构畸变，常见于$e_g$轨道电子数不均的配合物（如Cu²⁺的d⁹构型）

通过上述因素，可预测配合物的磁性、结构及光谱性质，理解过渡金属化学的多样性