1 函数极限
- 函数极限的概念和极限的性质与计算
- 连续与间断点的概念和基本公式
- 等价无穷小常用的代换公式
- 函数极限与数列极限的区别
- 洛必达法则使用的条件
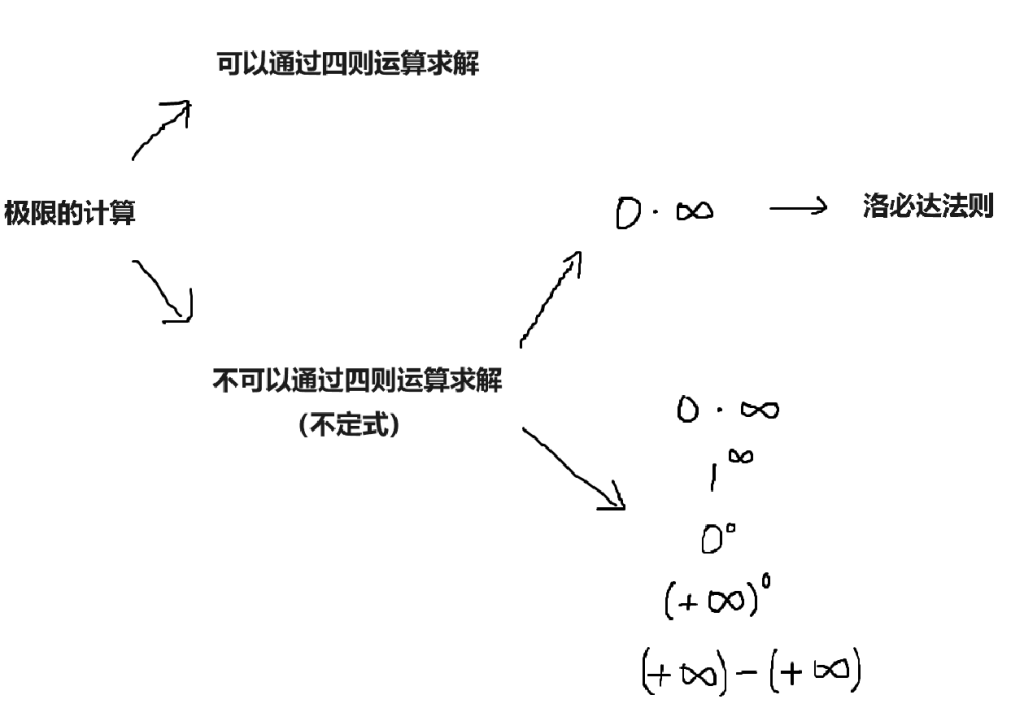
对于可以通过四则运算求解的极限，其要求为两个极限均存在.
1.1 基本方法
等价无穷小
$x\rightarrow0$时，
$$
\begin{aligned}
&\sin x \sim x \sim \sin x \sim \tan x \sim \arcsin x \sim \arctan x \sim (e^x-1) \\
&\ln x \sim (x-1) \\
& \ln(x+1)\sim x\\
& \log_a(1+x)\sim\frac{x}{\ln a}\\
& 1-\cos x \sim \frac{1}{2}x^2\sim x-\ln(1+x)\\
& x-\sin x\sim \arcsin x -x\sim \frac{1}{6}x^3\\
& \tan x -x\sim x-\arctan x \sim \frac{1}{3}x^3
\end{aligned}
$$
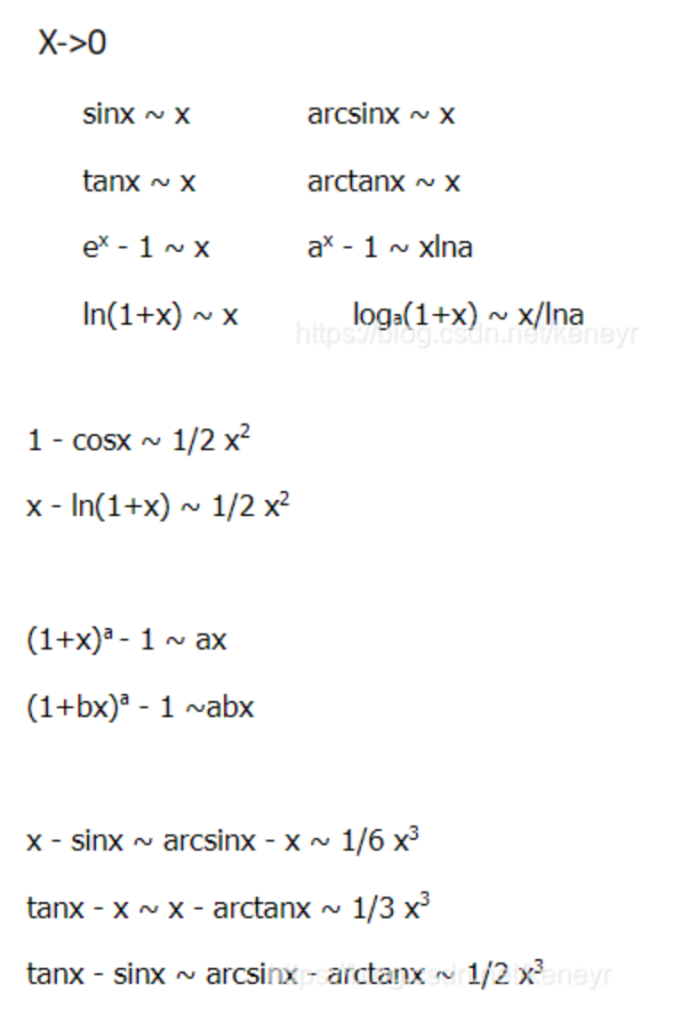
- 有关对数的等价无穷小
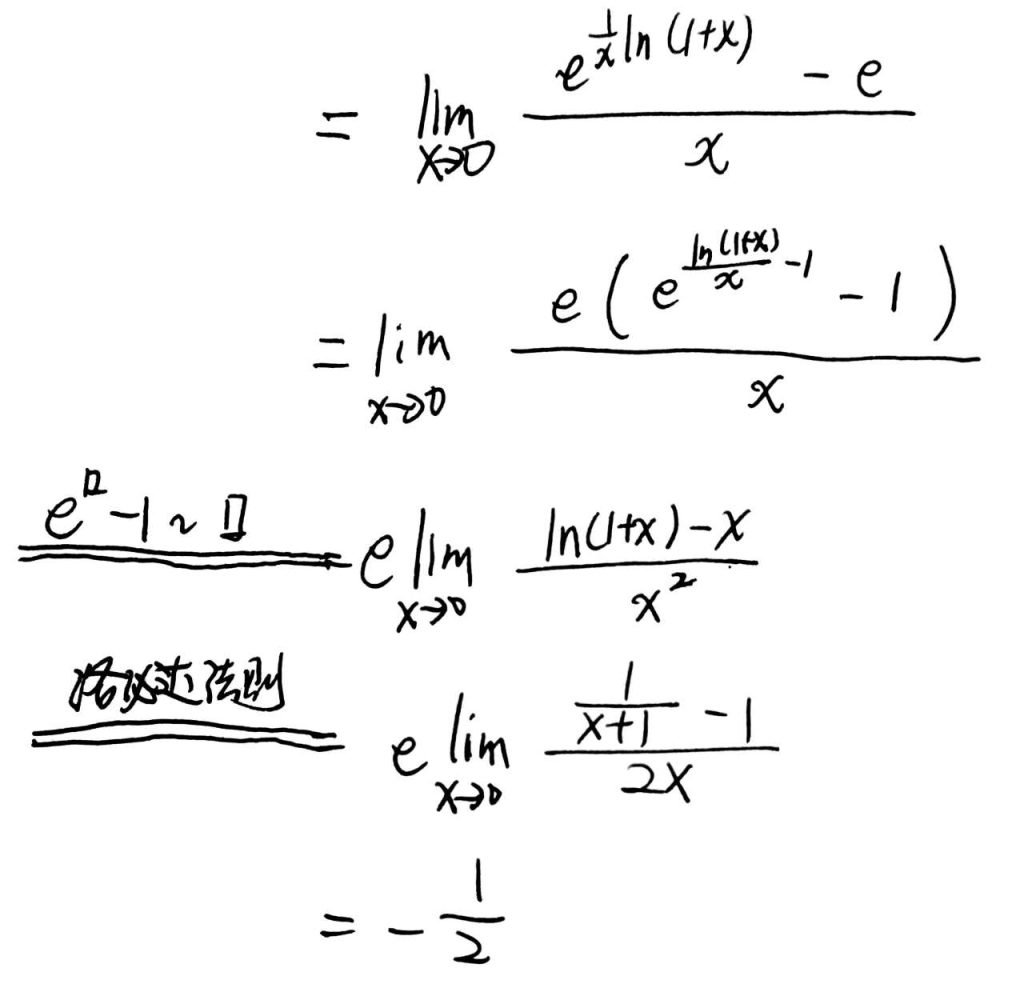
例题.
$$\lim_{x\rightarrow0}\frac{(1+x)^{\frac{1}{x}}-e}{x}$$
指数替换，再提出$e$，再用洛必达即可求解.
利用无穷小与无穷大的关系求极限
- 无穷小于无穷大的关系
$$\frac{1}{0}=\infty,\ \frac{1}{\infty}=0$$
无穷大$\infty$不允许出现在极限的四则运算中，因此必须通过变形将其转换为无穷小$0$.
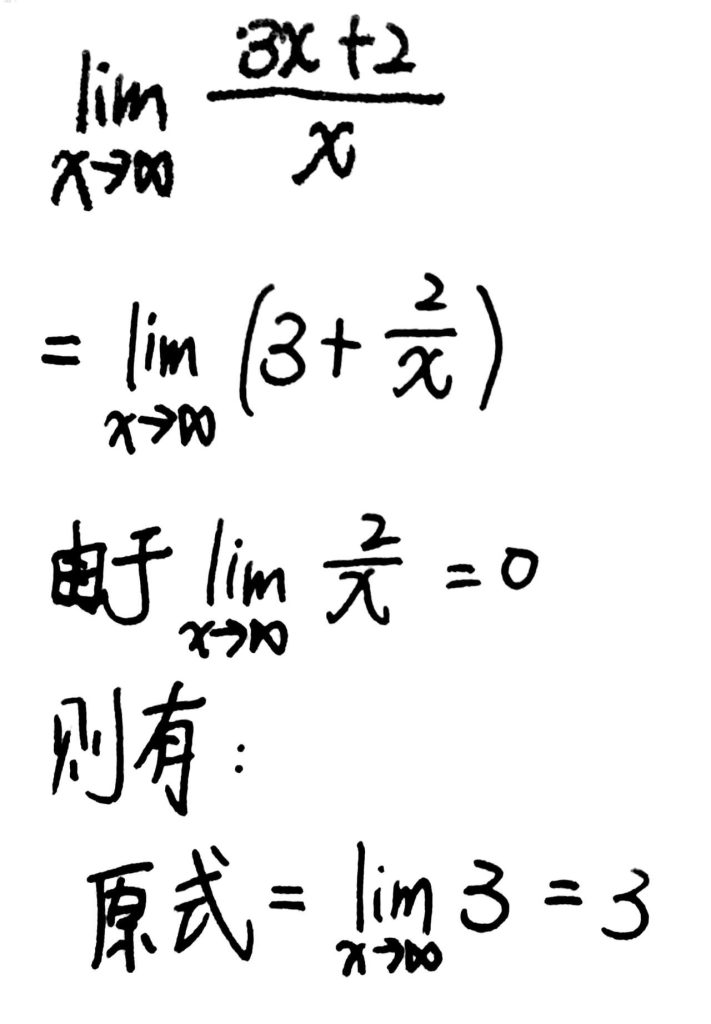
$$无穷小\times有界函数=无穷小$$
重要极限公式
- $\lim_{x\rightarrow\infty}{(1+\frac{1}{x})}^x=e$
例题. $\lim_{x\rightarrow\infty}\left(\frac{x+3}{x+2}\right)^{2x-1}$
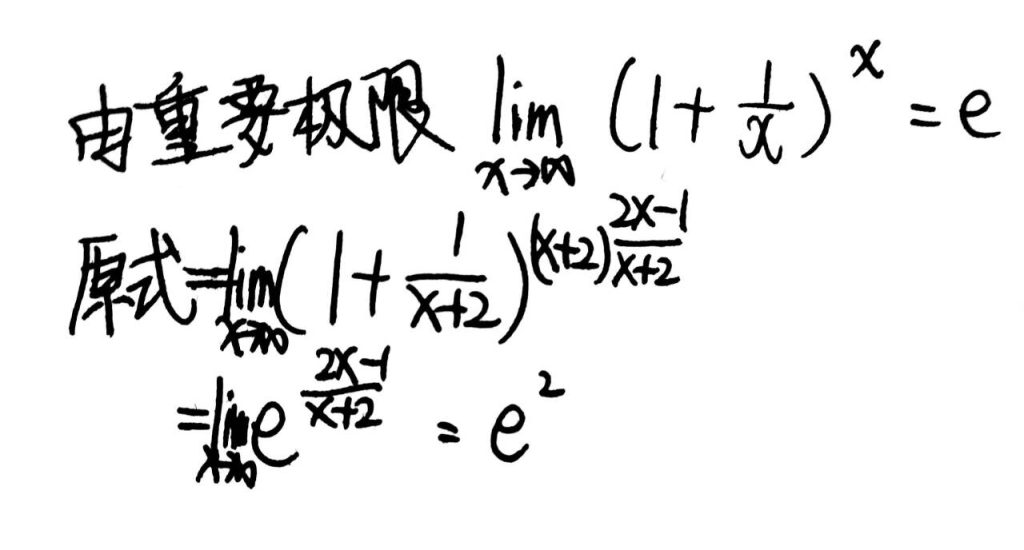
- $\lim f(x)^{g(x)}=e^{\lim g(x)\ln f(x)}$
若$\lim f(x)=1$，且$f(x)\ne1$，则$\lim f(x)^{g(x)}=e^{\lim g(x)[f(x)-1]}$.
以上这个推广变换形式，也是基于等价无穷小的：$x\rightarrow0,\ln x \sim x-1$.
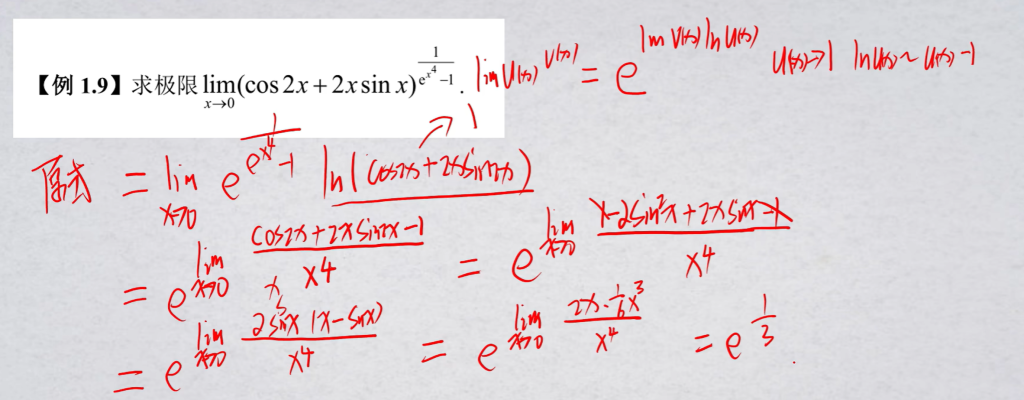
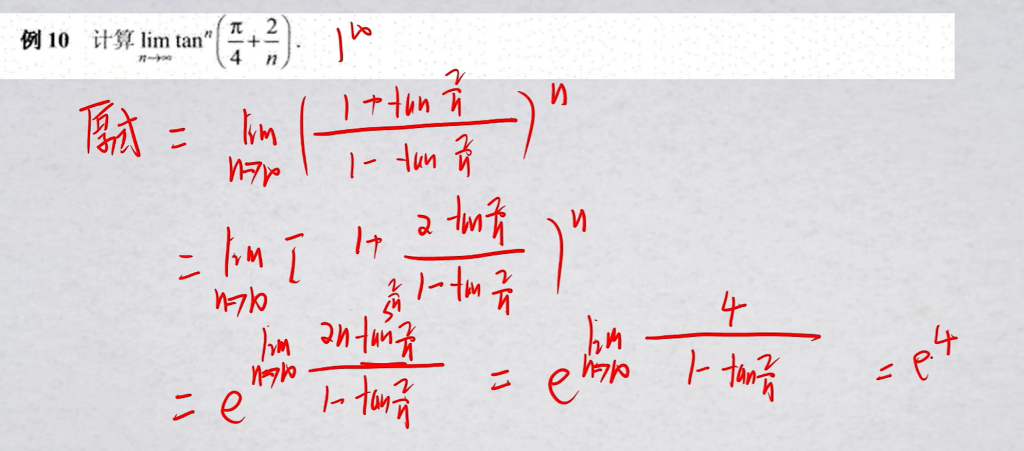
泰勒展开
泰勒公式的组成部分：
- Polynomials $\sum_{n=0}^{\infty}(x-a)^{n}$
- derivative $\sum_{n=0}^{\infty}f^{n}(a)$
- factorial $\sum_{n=0}^{\infty}\frac{1}{n!}$
$x=x_0$处，有近似
$$f(x)=\sum_{n}f(x_0)=\frac{f^{(n)(x_0)}}{n!}(x-x_0)^{(n)}$$
特别地，$x_0=0$时，称为麦克劳林展开式.
1.2 变形技巧
和式极限拆分
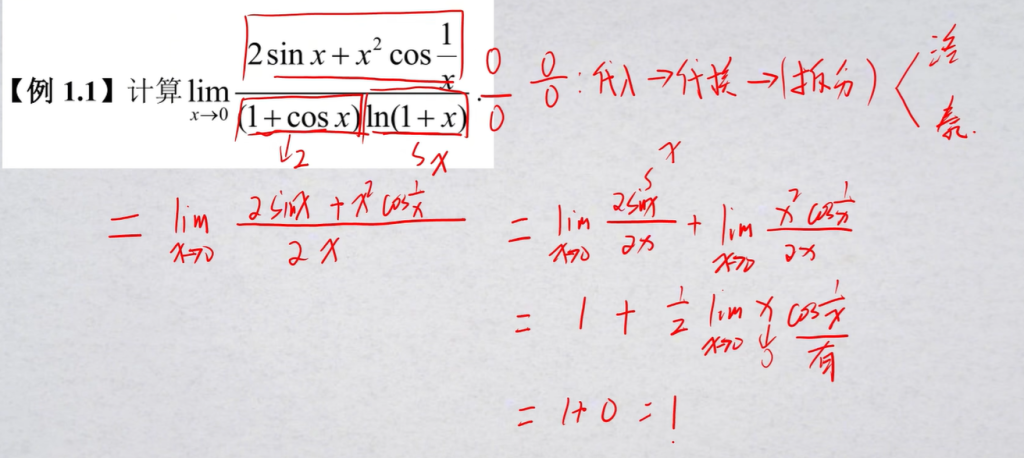
本题中，$\lim_{x\rightarrow0}x\cos\frac{1}{x}=0$，用到了重要概念：
$$无穷小\times有界=无穷小$$
同底指数代换
$$e^{b}-e^{a}=e^a(e^{b-a}-1)$$
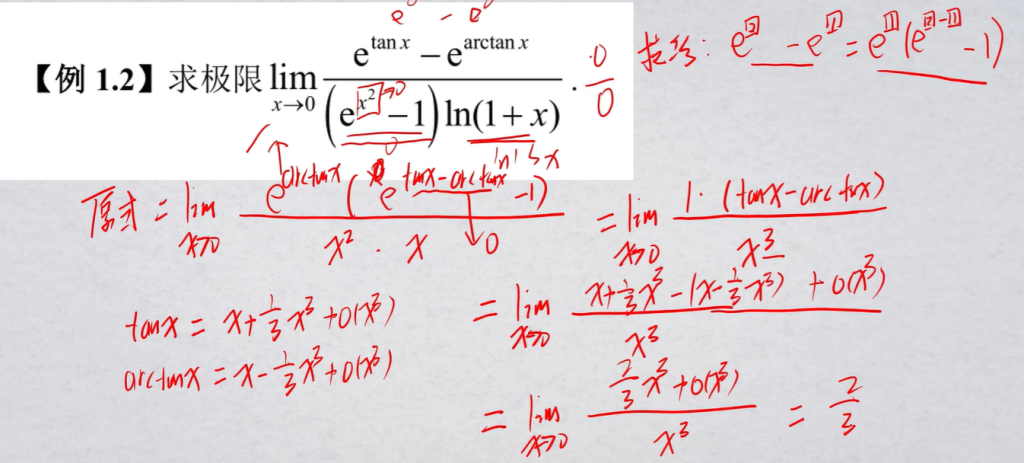
舍余项
低阶幂可以舍弃.
换元
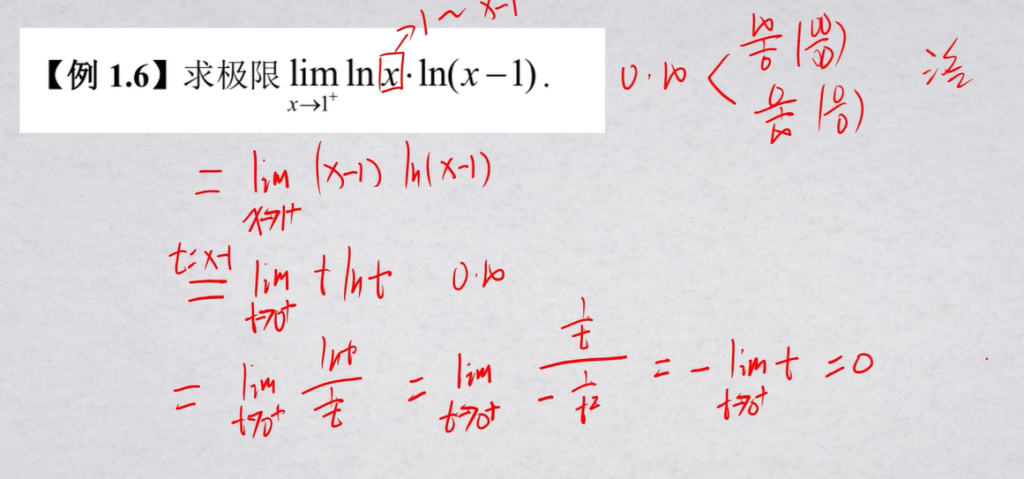
这道题同时考察了等价无穷小＋洛必达法则的应用.
换元和有理化可以互通，这道题用有理化也可解出.
第二步开始可以直接洛必达.
1.3 极限的其它问题
函数的连续
- 连续的定义
若$\lim_{x\rightarrow x_0}f(x)=f(x_0)$，则称函数$y=f(x)$在点$x_0$处连续. - 间断点
变限积分极限
$$
\left[\int_{u(x)}^{v(x)}f(t)dt\right]’=f[v(x)]v'(x)-f[u(x)]u'(x)
$$
无穷小的比较
- $\alpha$是$\beta$的高阶无穷小：$\lim_{x\rightarrow a}\frac{\alpha}{\beta}=0$，记为$\alpha=o(\beta)$
- $\alpha$是$\beta$的低阶无穷小：$\lim_{x\rightarrow a}\frac{\alpha}{\beta}=\infty$
- $\alpha$是$\beta$的同阶无穷小：$\lim_{x\rightarrow a}\frac{\alpha}{\beta}=c\ne0$
- $\alpha$是$\beta$的等价无穷小：$\lim_{x\rightarrow a}\frac{\alpha}{\beta}=1$，记为$\alpha\sim \beta$
- $\alpha$是$\beta$的$k$阶无穷小：$\lim_{x\rightarrow a}\frac{\alpha}{\beta^{k}}=c\ne0$
该题目中包含常用结论：
若$n>m>0$，则有：
- $o(x^m)+o(x^n)=o(x^{m})$
- $o(x^m)\cdot o(x^n)=o(x^{m+n})$
- $x^m\cdot o(x^n)=o(x^{m+n})$
- $c\ne0,cx^n+o(x^n)\sim cx^n$
极限的逆问题
- $\lim\frac{\alpha}{\beta}=\exists$ 且 $\lim\beta=0\Rightarrow \lim\alpha=0$
- $\lim\frac{\alpha}{\beta}=\exists,\beta\ne0$ 且 $\lim\alpha=0\Rightarrow \lim\beta=0$
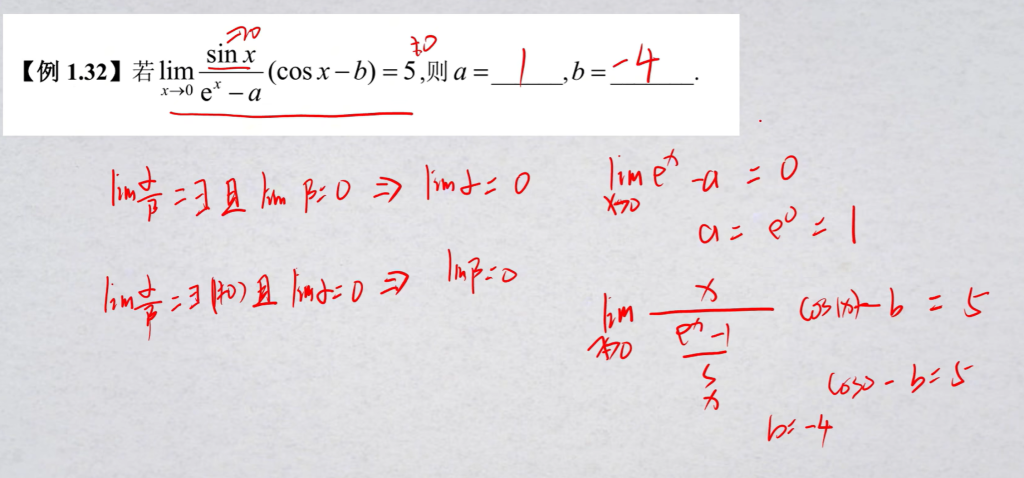
渐近线的求法
2 数列极限
2.1 夹逼准则
2.2 定积分定义
$$
\lim_{n\rightarrow\infty}\sum_{i=1}^{n}\frac{1}{n}f(\frac{i}{n})=\int_{0}^{1}f(x)dx
$$
对应关系：
$$
\begin{cases}
\lim_{n\rightarrow0}\sum\iff \int_{0}^{1}\\
\frac{1}{n}\iff dx\\
\frac{i}{n}\iff x
\end{cases}
$$
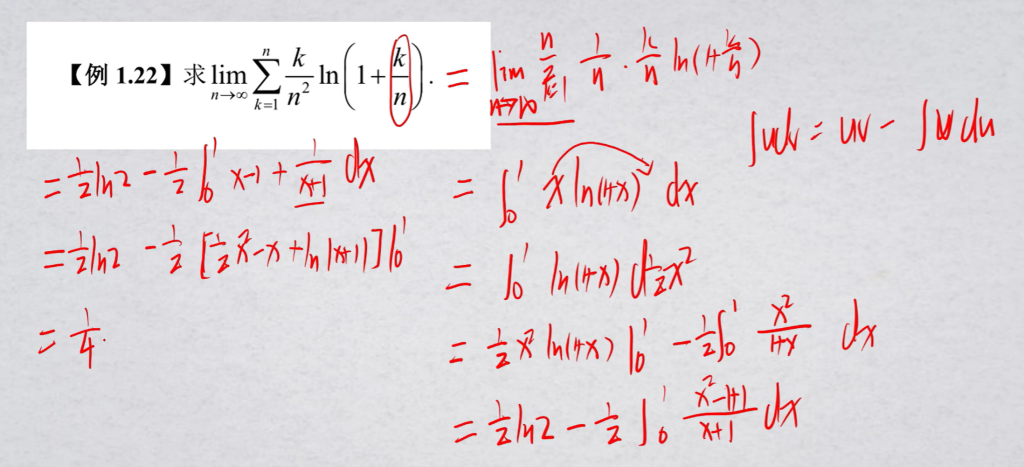
主要掌握转换方法即可.
2.3 单调有界准则
如果数列${x_n}$单调不减有上界（或单调不增有下界），则极限$\lim_{n\rightarrow\infty}x_n$一定存在.
3 导数与微分
3.1 求导
导数定义式
通过定义求解导数：
求某一点导数的时候，可以构造导数的定义式.
三角函数的求导
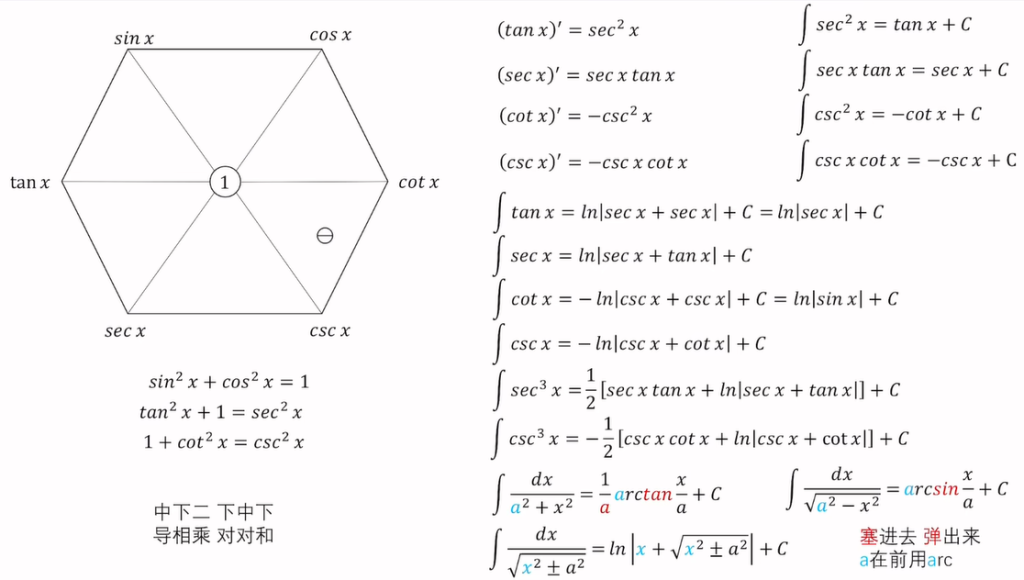
各类函数的求导方法
3.2 可微与可导
3.3 高阶导数的计算
常用高阶导数公式
$$y=e^{ax}, \ y^{(n)}=a^ne^{ax}$$
特别地，$(e^x)^{n}=e^x$
莱布尼茨公式
对于$u(x)\cdot v(x)$，若$n$阶导存在：
$$(uv)^{(n)}=C_{n}^{0}u^{(n)}v+C_{n}^{1}u^{(n-1)}v’+C_{n}^{2}u^{(n-2)}v”+\cdots+C_{n}^{n}uv^{(n)}$$
通过泰勒展开求高阶导
泰勒展开$n$阶，即可获得$n$阶导数.
4 中值定理
罗尔中值定理
若能找到两个点的函数值相等，就能找到某一点的导数为$0$.
对于证明题，连续和可导的条件基本都会给出，因此只需找到相等的两个端点以及原函数，然后对原函数使用罗尔中值定理.
- 基本步骤
- 移项
- 构造函数$F(x)$
构造原函数
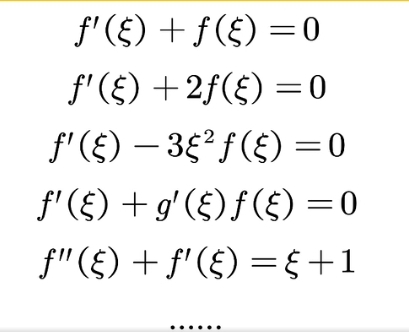
- 证明$f'(\xi)+f(\xi)=0$
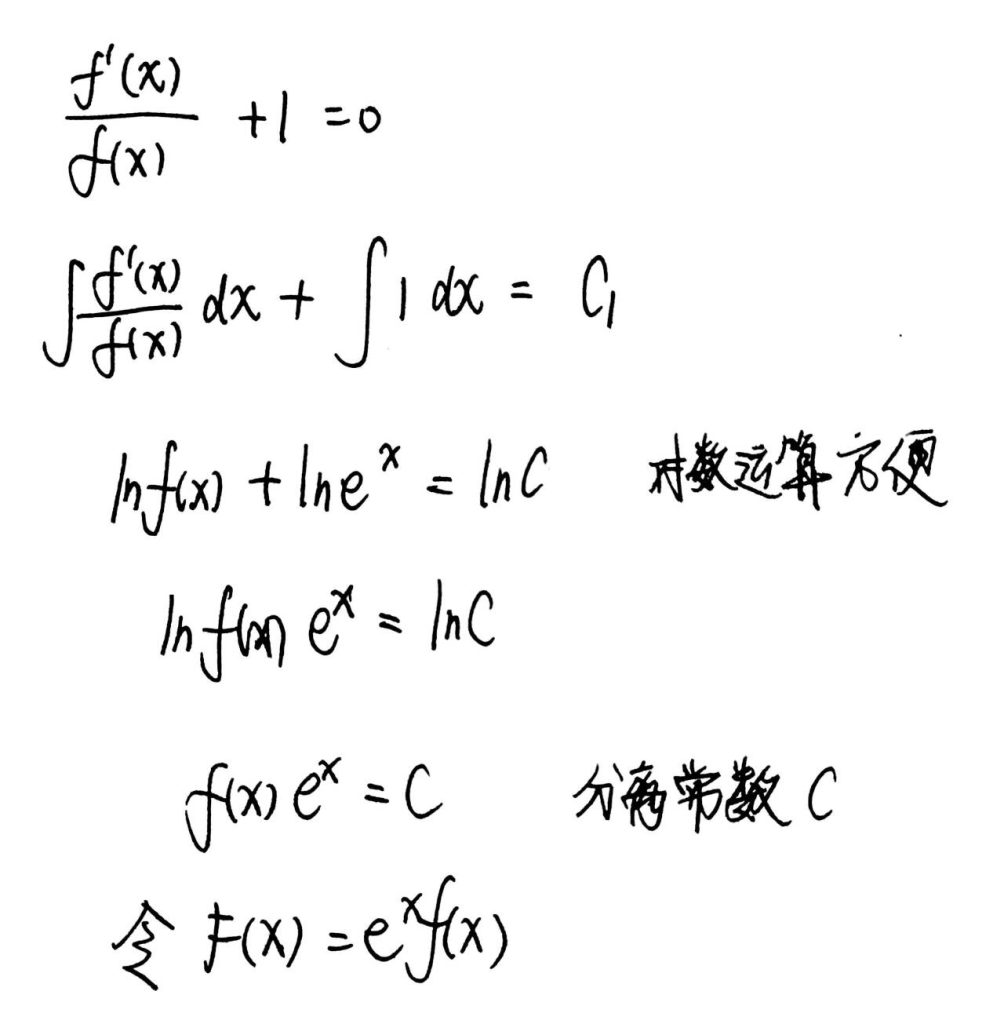
该模型可以拓展为 $f'(\xi)+g'(\xi)f(\xi)=0$ 的形式，其原函数为 $F(x)=e^{g(x)}f(x)$.
- 证明 $f”(\xi)+f'(\xi)=\xi+1$
积分中值定理
设函数$f(x)是[a,b]上的连续函数，则\exists \xi \in [a,b]$，使得
$$
\int_{a}^{b}f(x)dx=f(\xi)\cdot(b-a)
$$
定理证明
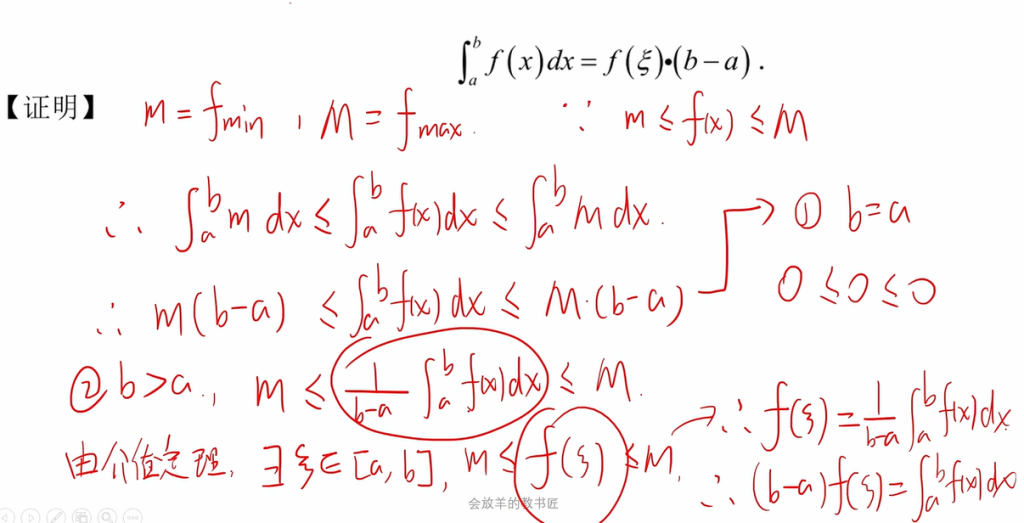
由连续函数的介值定理得证.
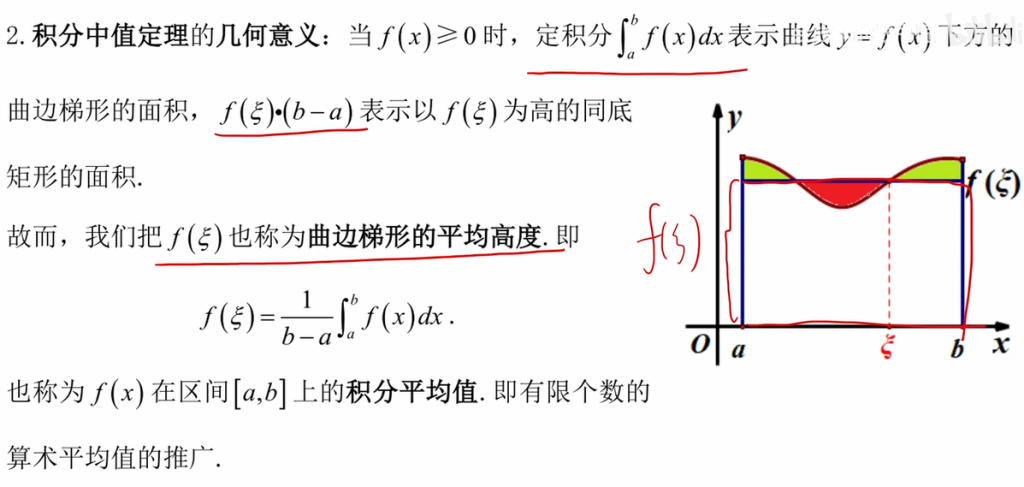
几何意义
由面积推导出：
$$曲边梯形的面积=平均高度\times底边长度$$
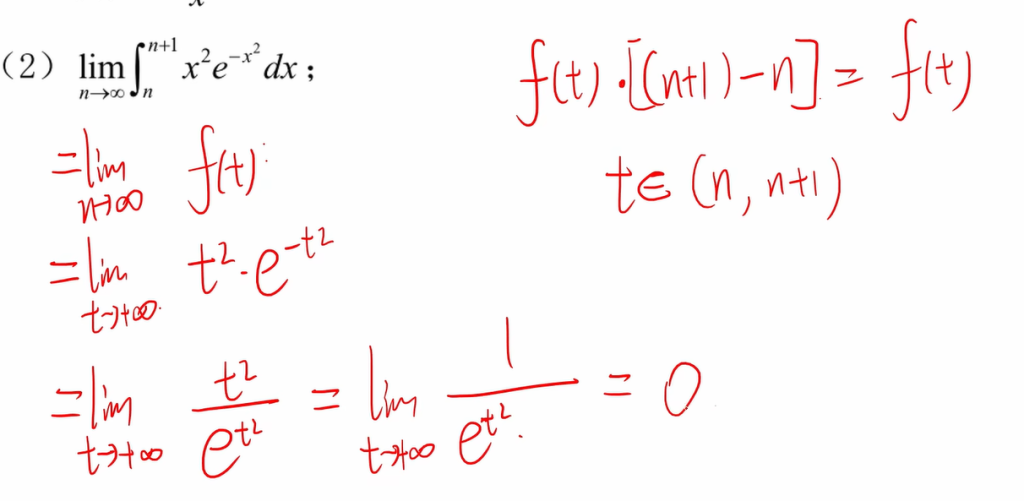
使用积分中值定理的目的就是去掉积分，本题还使用了洛必达法则.
5 一元积分学
5.1 基本方法
直接换元法
- 令$t=g(x)$
- 解出$x=f(t)$：为了替换$dx$，也是为后面回代$x$做准备
- 替换$dx$为$df(t)$
- 求解针对$dt$的积分
- 回代$x$，得到最终积分
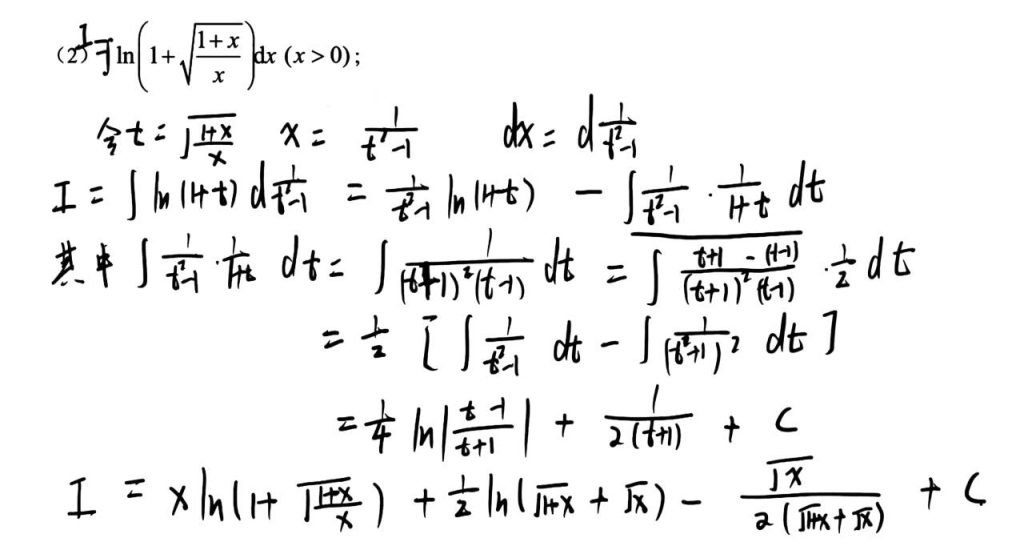
第二类换元：含根号问题
三角换元
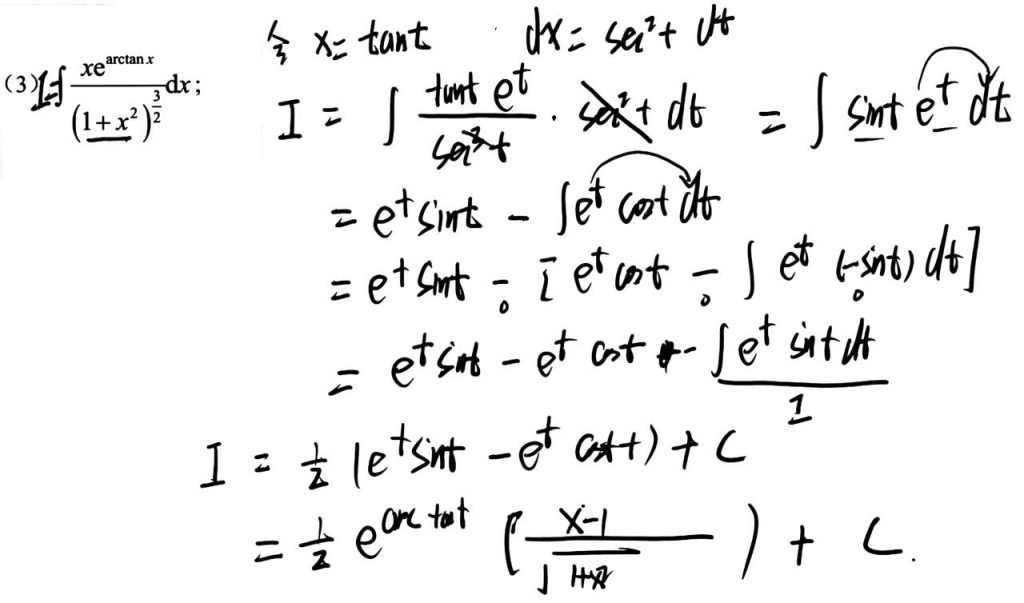
分部积分
分部积分是转换积分对象，即将求解较困难的$\int uv’dx$转换为求解较容易的$\int u’vdx$.
核心思想：令求导更容易的函数为$u$，令求原函数更容易的函数为$v$（$v$即为原函数形式了）
和式极限
变限积分
积分上下限含变量.
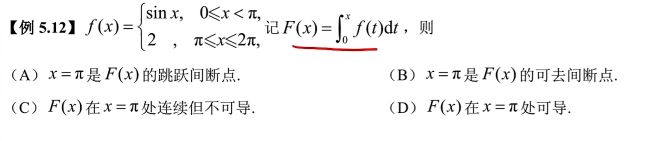
对于A选项：定积分是面积，当$x$趋近于$\pi$时，$F(x)$表示的面积与$F(\pi)$表示的面积之差越来越小，直到最后面积差为0.
对于C选项：定积分必连续，但是不一定可导，所以正确.
5.2 常用技巧
利用奇偶性和周期性化简后求解定积分的值
$$偶倍奇零$$
在$[0,1]$区间内，定积分和数列的和式极限可以相互转化，其中每个元素都有一一对应关系.
不定积分的基本思想即是化归，即将复杂积分转化为简单积分.
积分区间再现
直观上理解：从左往右积 和 从右往左积 结果相同
6 多元函数微分学
6.1 可微与极限
二元函数的极限
二元函数存在的条件：从任何路径趋近于某一定点时，极限都存在且相等.
可微定义的极限形式
其中$A=\frac{\partial z}{\partial x},B=\frac{\partial z}{\partial y}$.
二元函数极限也可以按照情况用等价无穷小.
6.2 多元函数求导
二阶偏导数的计算
例题.
由$f(u,v)$有连续的二阶偏导，可推出：
$$
\frac{\partial^2 z}{\partial x\partial y}=\frac{\partial^2 z}{\partial y\partial x}
$$
对于此种二阶混合导数，将$\partial$看作算子，即$\frac{\partial^2 z}{\partial x\partial y}=\frac{\partial}{\partial x}(\frac{\partial z}{\partial y})$.
先对$x$求偏导，再用结果对$y$求偏导.
不过在这道题中，计算顺序无所谓.
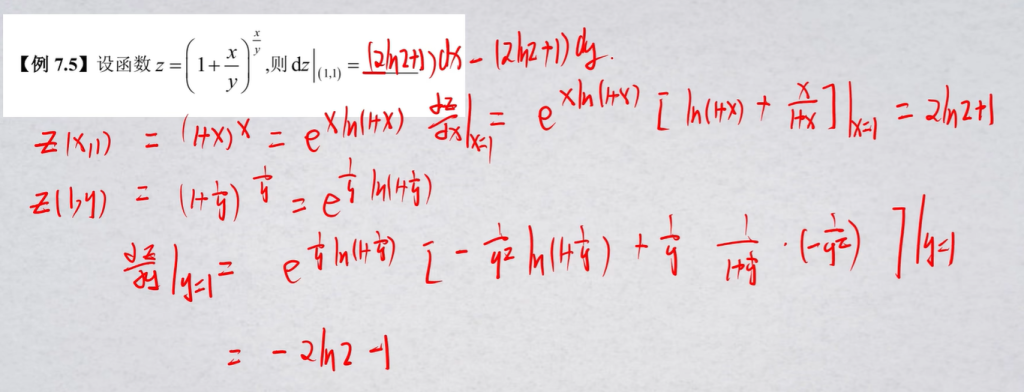
二阶混合偏导$\frac{\partial^2z}{\partial x\partial y}$
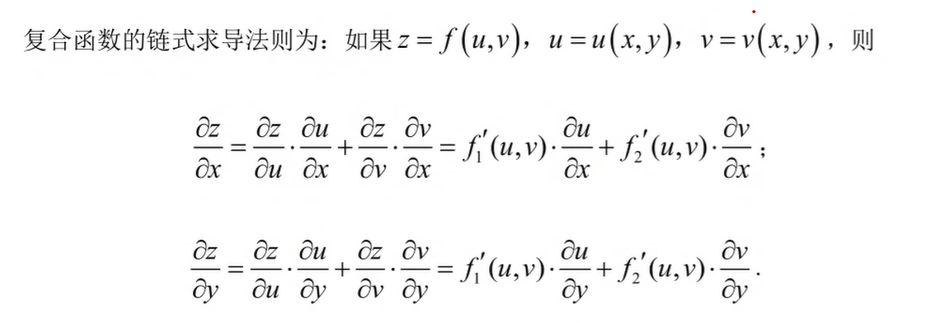
其它一元函数与多元函数复合情形和多元函数与多元函数复合情形与此类似，通常通过树形图分析变量之间的关系.
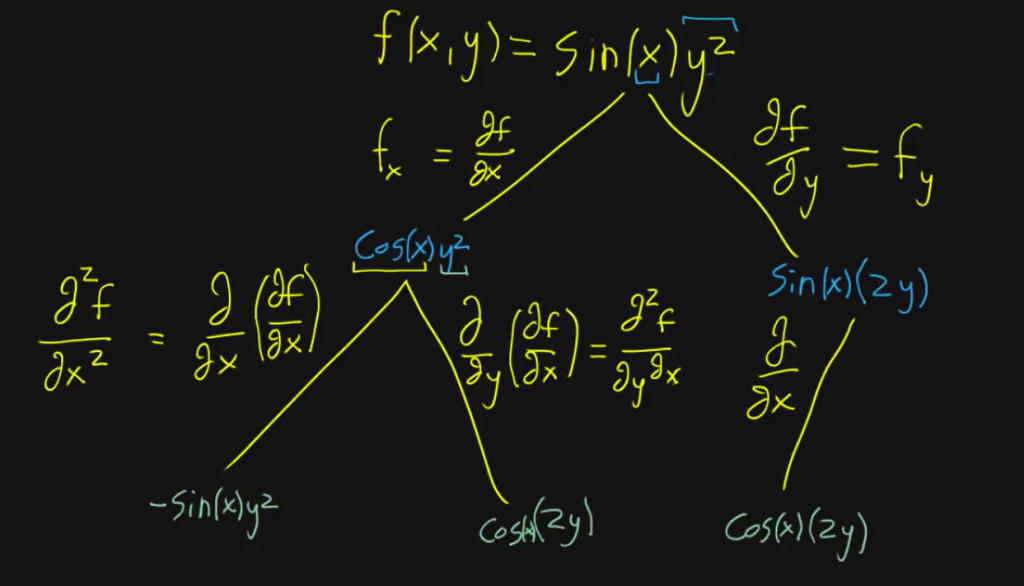
对于$z=f(x^2y,xy^2,y)$，求其二阶混合偏导$\frac{\partial^2z}{\partial x\partial y}$：
$$\frac{\partial z}{\partial x}=f_1’\cdot 2xy+f_2’\cdot y^2$$
其中$f_1’$为$f_1(x^2y,xy^2,y)’$的简写，即关于原复合函数第一部分的偏导，与原函数有相同的复合结构.
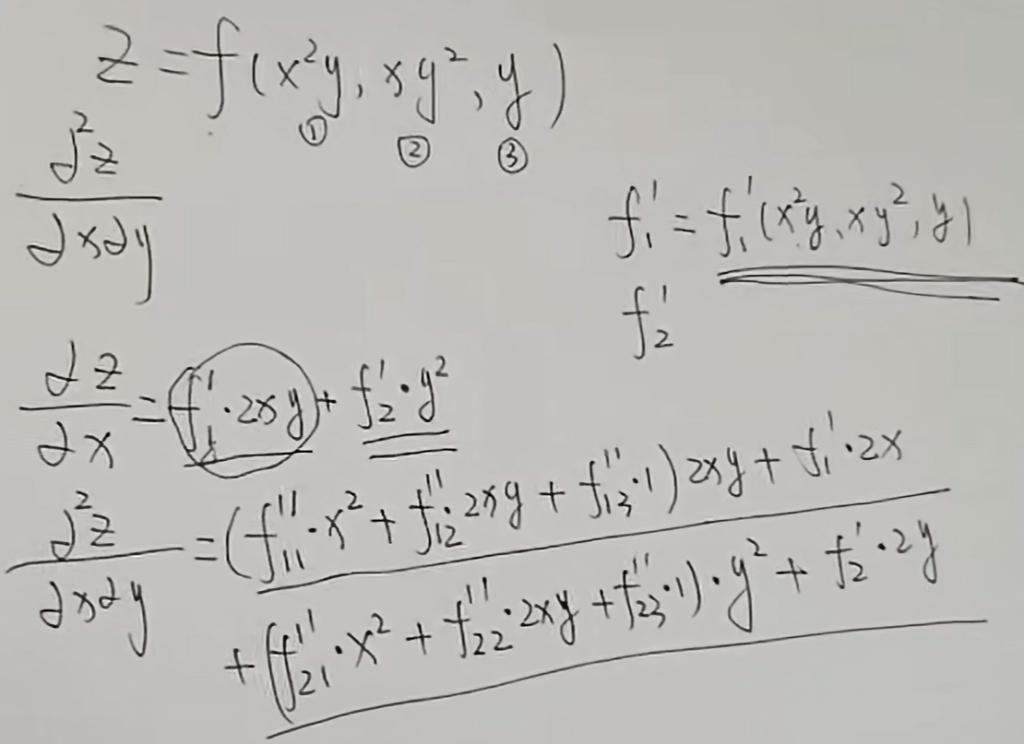
tips：混合偏导连续时与次序无关
7 二重积分
7.1 基本计算
线面积分归根结底也是二重积分.
发现被积函数复杂，那么就考虑换元，最常用的、最好用的就是极坐标换元.
对于二重积分，要先画出被积区域，如果忽略这一步，做题就免谈了.
比较大小
积分区域相同时，被积函数越大，则积分结果越大.
被积函数相同，积分区域越大，则积分结果越大.
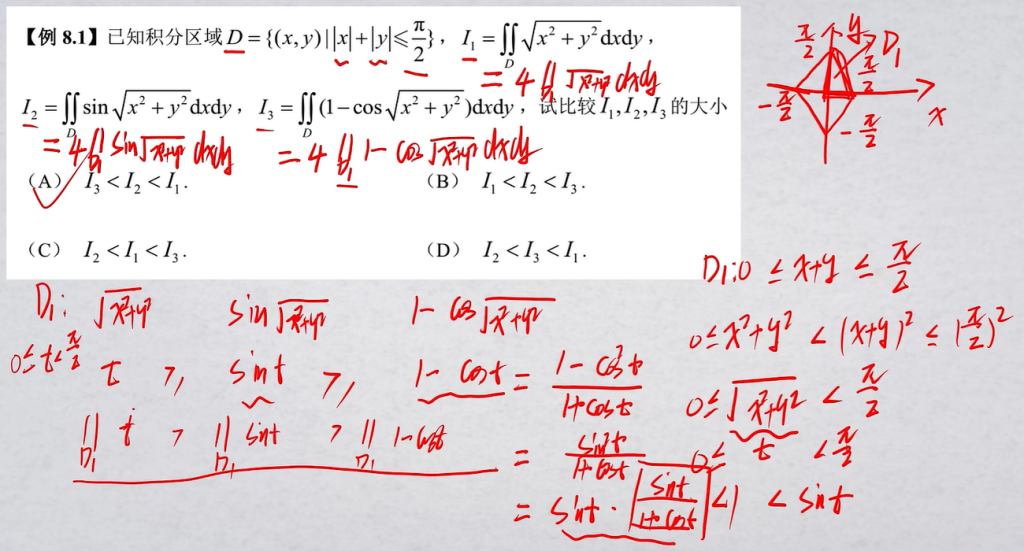
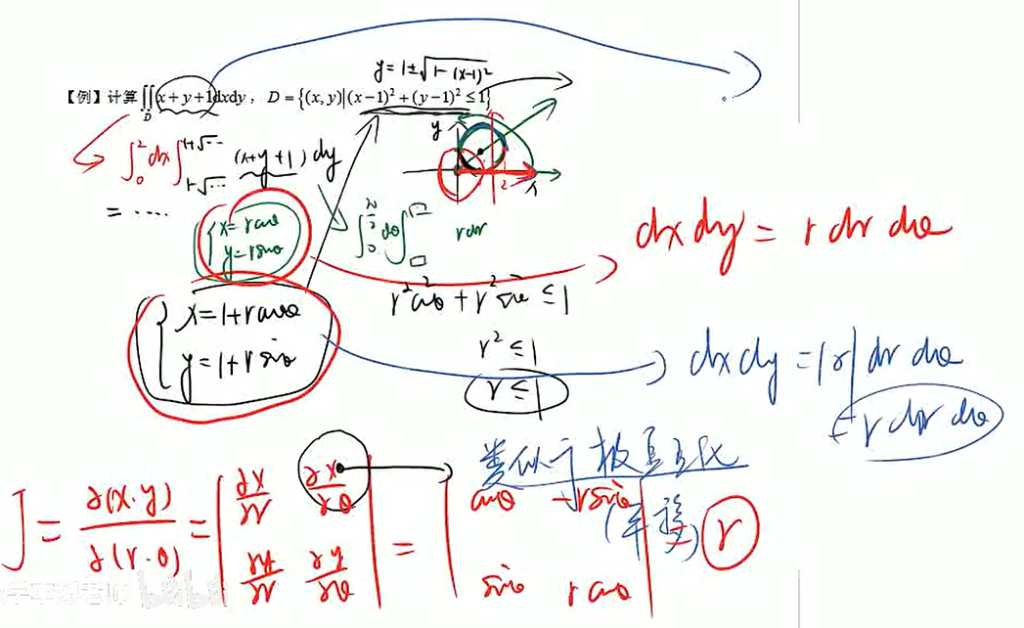
雅可比行列式
雅可比行列式的基本思想，是将不规整的积分域，通过拉伸、扭曲，投射到另一个空间，使其变得更为规则、便于积分.
事实上，行列式的几何意义，就是对应矩阵线性变化后面积的拉伸比.
若$x=x(u,v),y=y(u,v)$存在偏导数，则二阶雅可比行列式为
$$
J=\frac{\partial(x,y)}{\partial(u,v)}=\left|\begin {array}{c}
\frac{\partial x}{\partial u} &\frac{\partial x}{\partial v} \\
\frac{\partial y}{\partial u} &\frac{\partial y}{\partial v}
\end{array}\right|
$$
积分微元$dxdy=|J|dudv$（$J$取绝对值）且
$$
\iint_{D_{xy}}f(x,y)dxdy=\iint_{D_{uv}}f[x(u,v),y(u,v)]|J|dudv
$$
其中积分域$D_{xy}$与$D_{uv}$一一对应.
极坐标换元的$dxdy=rd\theta dr$，本质上也是基于雅可比行列式的：
类似极直变换的雅可比换元：
$\iint_D \frac{(x+y)\ln(1+\frac{y}{x})}{\sqrt{1-x-y}}dxdy$，其中区域$D$是由直线$x+y=1$与两坐标轴所围三角形区域.
对称性与轮换法则
轮换对称性：交换两个变量后，方程不变.
例如对于$\iint_{D}(x^2+2y^2+3x^2)dS,D=x^2+y^2+z^2=2y$，交换$x$和$z$后方程不变，这就是$x$和$z$具有轮换对称性.
7.2 曲线积分
- 积分限
- 被积函数
- 积分元素
第一类曲线积分
可以将被积函数理解为线密度.
- 若平面曲线$L$的质量密度为$f(x,y)$，则$L$的质量$M=\int_{L}f(x,y)ds$
- 若平面曲线$\Gamma$的质量密度为$f(x,y)$，则$\Gamma$的质量$M=\int_{\Gamma}f(x,y,z)ds$
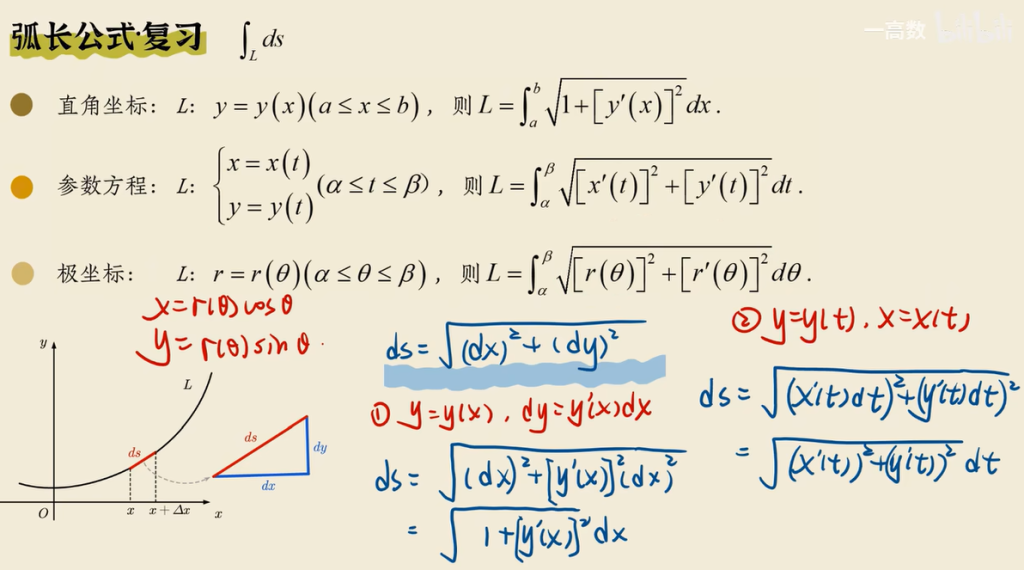
三元函数情形例题：
分别代入$x,y,z$，再将$dS$（本质上是替换为$dt$）后即可计算.
- 总结
- 普通对称性
7.3 曲面积分
- 基本方法
选择适当的曲面方程化两类曲面积分为二重积分
- 基本技巧
两类曲面积分的转换，高斯公式与斯托克斯公式的灵活运用
第一类曲面积分的计算
曲面的面积
设曲面$S$对应的函数为$f(x,y)$，$D$为曲面$S$在$xOy$面上的投影区域，函数$f(x,y)$在$D$上具有连续偏导数$f_x(x,y)$和$f_y(x,y)$，则曲面$S$在$D$上的面积$A$为：
$$
A=\iint_D\sqrt{1+f_x^2+f_y^2}d\sigma
$$
其中$\sqrt{1+f_x^2+f_y^2}d\sigma$记作$dA$，称为曲面$S$的面积元素.
tips：利用对称性及曲面方程化简被积函数.
8 无穷级数
8.1 基本级数与收敛证明方法
$p$级数
- $\frac{1}{n^p}$>1, 则$\sum_{n=1}^{\infty}\frac{1}{n^p}$收敛
- $\frac{1}{n^p}\leq1$, 则$\sum_{n=1}^{\infty}发散$
- 特别地，对于$\frac{1}{n^p\ln^n{\beta}}$：
- $beta>1$时，$\sum_{n=1}^{\infty}\frac{1}{n^p\ln^n{\beta}}$收敛
- $beta\leq1$时，$\sum_{n=1}^{\infty}\frac{1}{n^p\ln^n{\beta}}$发散
$q^n$
- 若$|q|<1$，则$\sum_{n=1}^{\infty}q^n$收敛
- 若$|q|\leq1$，则$\sum_{n=1}^{\infty}q^n$发散
比较判别法
人话：两个级数比较所得极限，若等于非$0$常数，则散敛性一致.
莱布尼茨判别法
若$\lim_{n\rightarrow \infty}u_n=0$且$u_{n+1}<u_n$，则$\sum_{n=1}^{\infty}(-1)^n\cdot u_n$收敛.
人话：若$u_n$趋于零且单调递减，则$\sum_{n=1}^{\infty}(-1)^n\cdot u_n$收敛
8.2 幂级数的收敛半径和收敛域
形如$\sum_{n=0}^{\infty}a_n(x-x_0)^n$，下面均考虑$\sum_{n=1}^{\infty}a_nx^n$
Cauchy根值法
$$\lim_{n\rightarrow\infty}{}^n\sqrt{|a_n|}=A$$
$$
R=
\begin{cases}
+\infty,\ \ &A=0\\
\frac{1}{A},\ \ &a\in(0,+\infty)\\
\ 0,\ \ &A=+\infty
\end{cases}
$$
- 解题方法
本质：后项比前项，利用比较判别法判定
令$\rho=\lim_{n\rightarrow\infty}\left|\frac{a_{n+1}}{a_n}\right|$，则有：
$$
\begin{cases}
\ 0,\ \ \ &\rho=+\infty\\
+\infty,\ \ \ &\rho=0\\
\frac{1}{\rho},\ \ \ &\rho\ne0
\end{cases}
$$
- 对于$\sum_{n=1}^{\infty}a_nx^n$，收敛区间为开区间$(-R,R)$
- 将$x=\pm R$代入原级数，判断端点处的敛散性，写出收敛域
d’Alembert判别
- 求$R$
- 求端点
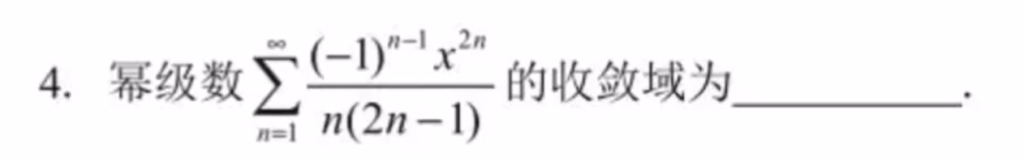
9 微分方程
9.1 一阶微分方程
分离变量
齐次方程
可化为变量可分离的方程.
形如$\frac{dy}{dx}=f(\frac{y}{x})$，令$\frac{y}{x}=u$，则$\frac{dy}{dx}=u+x\frac{du}{dx}=f(u)$
得通解为$$\int\frac{du}{f(u)-u}=\int\frac{dx}{x}\ln|x|+C$$
步骤解析
一阶线性微分方程
形如$y’+p(x)y=q(x)(q(x)\ne0)$，通解公式为$y=e^{-\int p(x)dx}dx+C$
9.2 高阶微分方程
缺$y$类型：
Refrence
【超哥的考研数学《三大计算》全讲解——典藏版（更新完毕）】
【2024大学生数学竞赛非数学类（AB） 初赛往届真题讲解】
【【数竞（非数类）】20天考前冲刺、考点全面分类总结+思路技巧 | 全国大学生数学竞赛轻松拿奖】
【数学笔记-第一章-极限】
【【全国大学生数学竞赛】非数学类历年真题刷题（高数版）】
【全网最细！雅克比行列式积二重积分！李老师一出手，你就知道这个知识点要懂了！】
【【高等数学】多元抽象复合函数求高阶偏导数（高清版）】
0 条评论