1 金属的应力-应变曲线
- 弹性变形:卸载后可以恢复
- 塑性变形:卸载后不可恢复
1.0 拉伸实验 Tensile Test
测量力与(拉伸)距离的关系
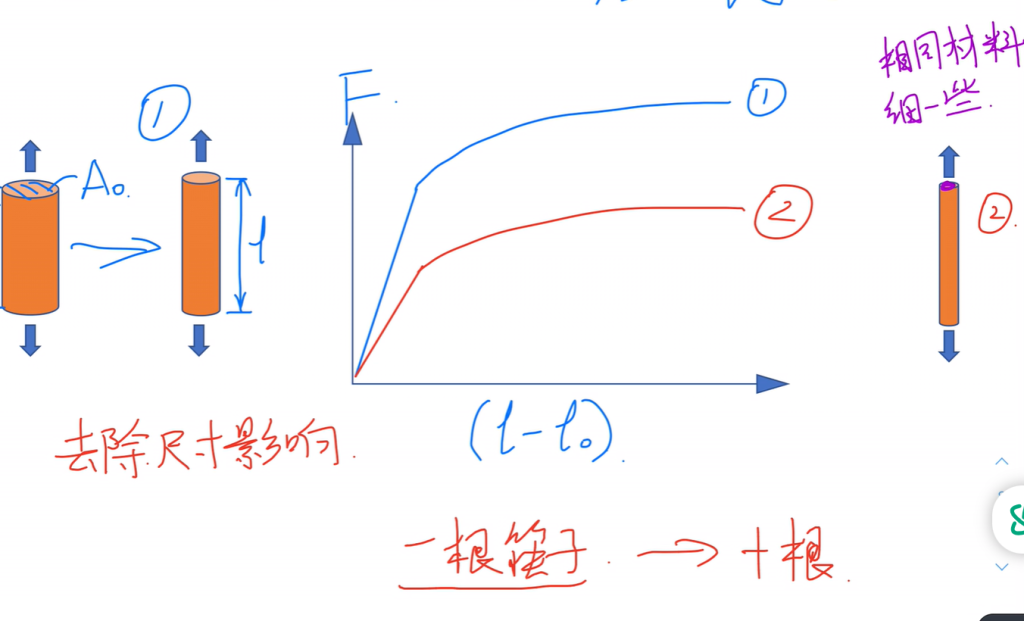
为了去掉材料尺寸的影响,就有了力-距离曲线到应力-应变曲线之间的转换.
1.1 工程应力-应变曲线 stress-strain curve
- 应力:$\sigma=\frac{F}{A_{unit}}(MPa)$ 单位面积所承受的力
- 应变:$\varepsilon=\frac{l-l_0}{l_0}(\%)$
引入应力、应变,就是为了消除材料尺寸的影响.
强度指标
弹性阶段,应力应变曲线呈至直线;在屈服阶段,由弹性形变向塑性形变过渡;直到进入塑性形变阶段,形变不可逆转;过最高点后进入颈缩阶段,最终断裂.
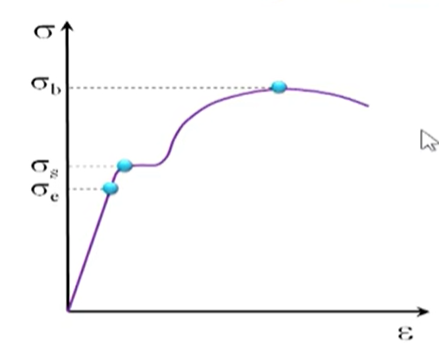
- 弹性极限 $\sigma_{e}$
- 屈服强度 $\sigma_{y}$
- 条件屈服强度 $\sigma_{0.2}$
- 抗拉强度 $\sigma_{uts}$(Ultimate Tensile Strenth)
- 延展性$\varepsilon_{f}$ (ductility):断裂位置的应变量
- 脆性(brittle):$\varepsilon_{f}<0.5\%$
- 韧性:$\varepsilon_{f}$越大,韧性越强
塑性指标
- 屈伸率 elongation
$$\delta=\frac{l_k-l_0}{l_0}$$
- 断面收缩率 reduction of area
$$\psi=\frac{A_0-A_k}{A_0}$$
胡克定律
$$\sigma=E\cdot \varepsilon$$
- 弹性模量
- 杨氏模量 $E$
- 剪切模量 $G$
弹性模量反应原子间结合力的大小
1.2 阶段分析
弹性形变
$$
\begin{aligned}
&\sigma=E\varepsilon\\
&\tau=G\gamma \\
&G=\frac{E}{2(1+\nu)}
\end{aligned}
$$
- 线性
应力和应变满足直线关系
- 可逆性
去掉外力,变形就消失
- 变形量
- 陶瓷材料的弹性变形量很小
- 金属材料的弹性变形量略大
- 高聚物材料的弹性变形可以比较大
影响弹性模量的主要因素
- 结构:弹性模量与原子序数呈周期性变化趋势
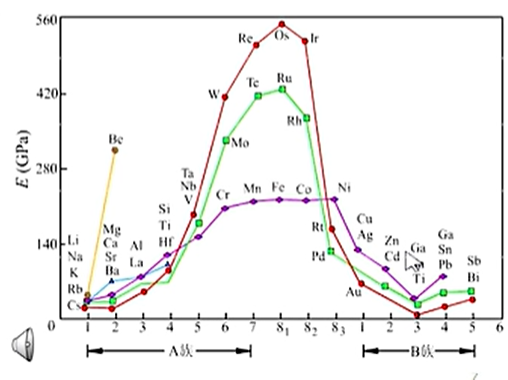
- 温度:$T$升高,$E$下降
- 合金元素:
- 对结构不敏感
- 少量合金元素不影响
颈缩与断裂阶段
$\sigma$经过最高点后,材料通常开始发生颈缩和断裂.
颈缩是局部变细——在颈缩前,整个材料都会塑性变形,但在颈缩后,只有颈缩部位是塑性变形,其他部位不会有塑性变形.
1.3 真应力-真应变曲线
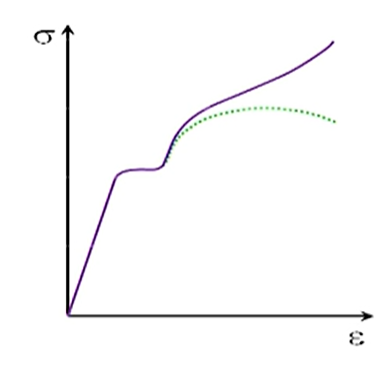
由$\sigma=\frac{F}{A_0},\varepsilon=\frac{\Delta l}{l_0}=\frac{l_0′-l_0}{l_0}$所得到应力和应变;然而由于$l_i,A_i$每时每刻都会变化,因此理论应力应变和实际应力应变并不相同.
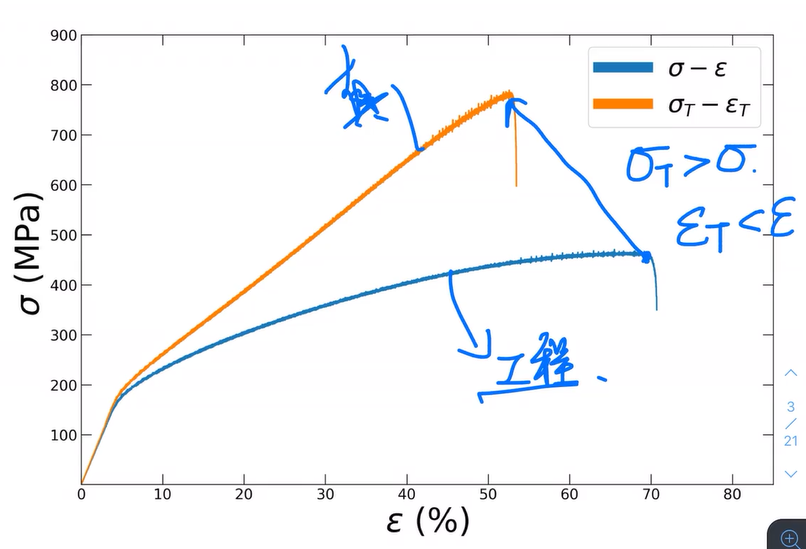
真应变
$$
\begin{aligned}
& \varepsilon_T=\int d\varepsilon=\int_{l_0}^{l_i}\frac{dl}{l}=\ln l_i-\ln l_0\\ \\
& \sigma_T=\ln(1+\varepsilon)
\end{aligned}
$$
其中$\varepsilon$为工程应变.
由此得到真应变和工程应变的关系.
真应力
由于变形过程中体积不变,
$$
\begin{cases}
& l_o\cdot A_0=l_i\cdot A_i\\ \\
& \varepsilon=\frac{l_i-l_0}{l_0}
\end{cases}
\ \Rightarrow
l_i=l_0(1+\varepsilon)\ \ \
\Rightarrow A_i=\frac{A_0}{(1+\varepsilon)}
$$
其中$\varepsilon$为工程应变,由此可推知真应力(true stress):
$$
\sigma_T=\frac{F}{A_i}=\frac{F}{A_0}\cdot(1+\varepsilon)=\sigma(1+\varepsilon)
$$
其中$\sigma$为工程应力.
流变曲线
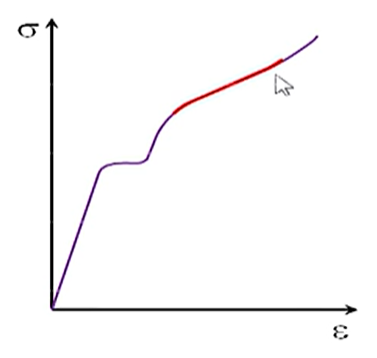
$$ S=ke^n $$
- $k$:常数
- $n$:形变硬化指数,表示抵抗继续塑变的能力
2 单晶体的塑性变形
2.1 塑性变形的微观本质
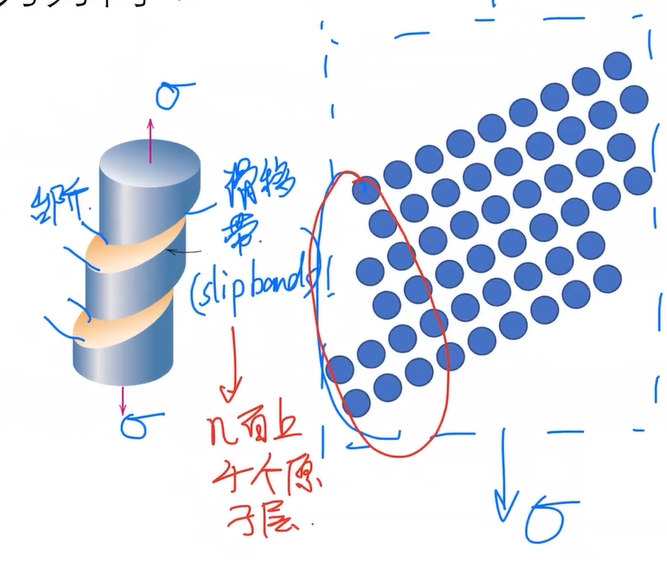
滑移
塑性变形是晶体沿着某个特定的晶面和晶向发生的一种平行错动,这种错动即为滑移.
- 滑移面:可以发生滑移的晶面
- 滑移方向:可以发生滑移的晶向
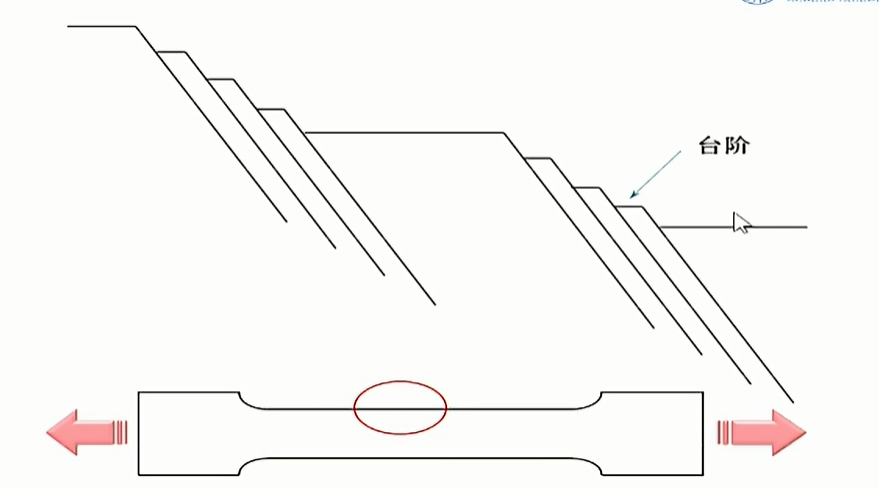
滑移线聚集的地带,即为滑移带.
滑移系
一个滑移面及其上的一个滑移方向构成的一个空间位向关系.
- 条件相同时,滑移面越多,塑性越好
- 条件相同时,滑移方向越多,塑性越好
一般来说,最密排方向即为滑移方向,最密排面即为滑移面.
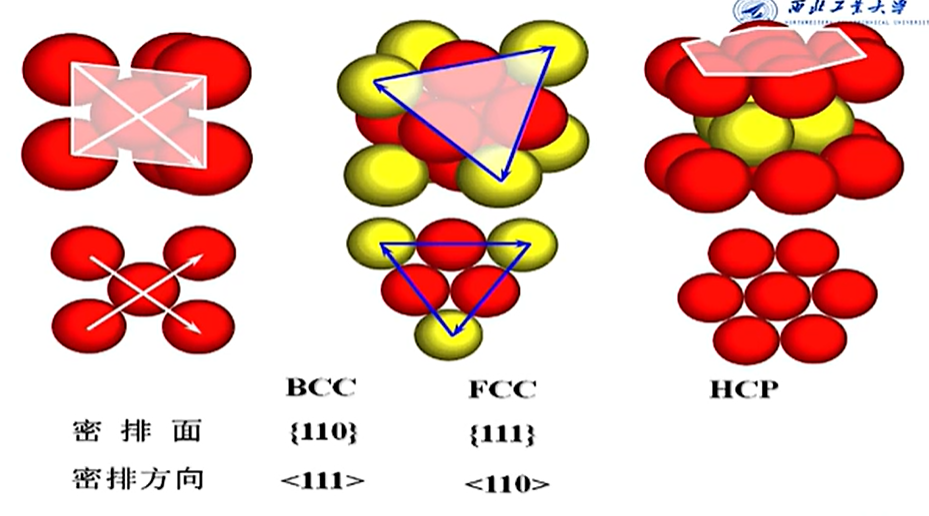
补充:$HCP$密排面$\{0001\}$,密排方向$<11\overline{2}0>$
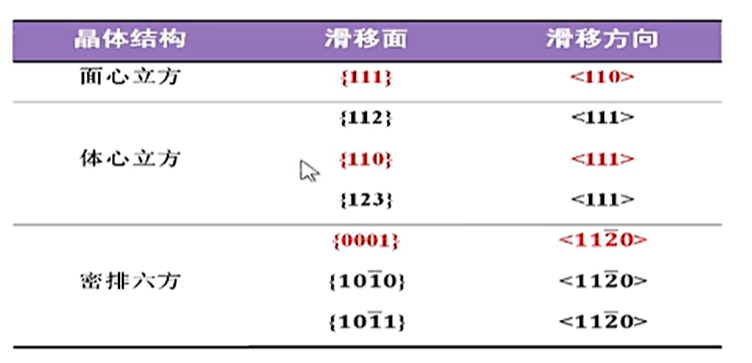
2.2 临界分切应力
剪切分量$\tau$
取向因子 Schmid factor
$$
\tau=\sigma\cos\phi\cos\lambda
$$
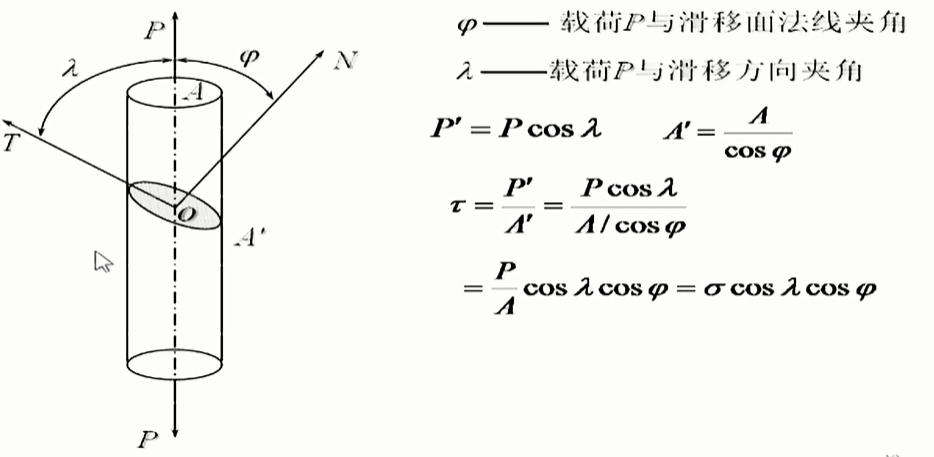
$$\tau=\sigma\cos\lambda\cos\varphi$$
屈服应力$\sigma_s$(或$\sigma_{0.2}$)
$$
\begin{aligned}
&\tau=\sigma\cos\lambda\cos\varphi\\
&\tau_c=\sigma_s\cos\lambda\cos\varphi
\end{aligned}
$$
- 晶体开始滑移所需的最小分切应力
- $\tau_c$取决于晶体的本性,与外力无关
- $\tau_c$是组织敏感参数
即与晶体类型、纯度、温度、热处理状态、滑移系类型等因素有关.
Summary:塑性形变是由于平行滑动的位错而产生的,滑动方向是最密排面和最密排方向.
refrence
材料科学基础 西北工业大学 王永欣93讲
【材料科学基础(易学版)-7.1 塑性变形和位错 (单晶)】
其他资源
泡泡模型:https://www.youtube.com/watch?v=UEB39-jlmdw&t=2s GATECH Kacher组的研究视频:https://kacherlab.gatech.edu/tools-for-teaching/ Cambridge的教学网站:https://www.doitpoms.ac.uk/tlplib/dislocations/index.php MIT一个课的讲义:https://ocw.mit.edu/courses/materials-science-and-engineering/3-11-mechanics-of-materials-fall-1999/modules/MIT3_11F99_dn.pdf 螺位错的简单模型:https://ocw.mit.edu/resources/res-3-004-visualizing-materials-science-fall-2017/student-projects-by-year/2017-MIT/visualizing-the-energies-of-screw-dislocations/visualizing-the-energies-of-screw-dislocations/
0 条评论