Note | 材料基 ch.断裂

断口的形成

韧性断裂 Ductile Fracture

发生断裂时，会产生明显的颈缩.

• covity
• dimples

韧窝的形成，从微观角度来看，韧性断裂超过屈服强度后产生滑移，从而使材料表面不断变薄，从而形成dimples.

滑移越充分，断口就越尖锐.

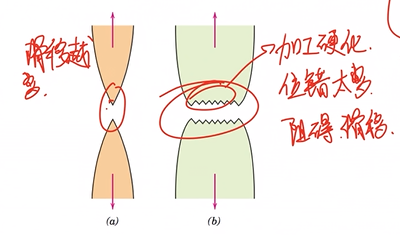
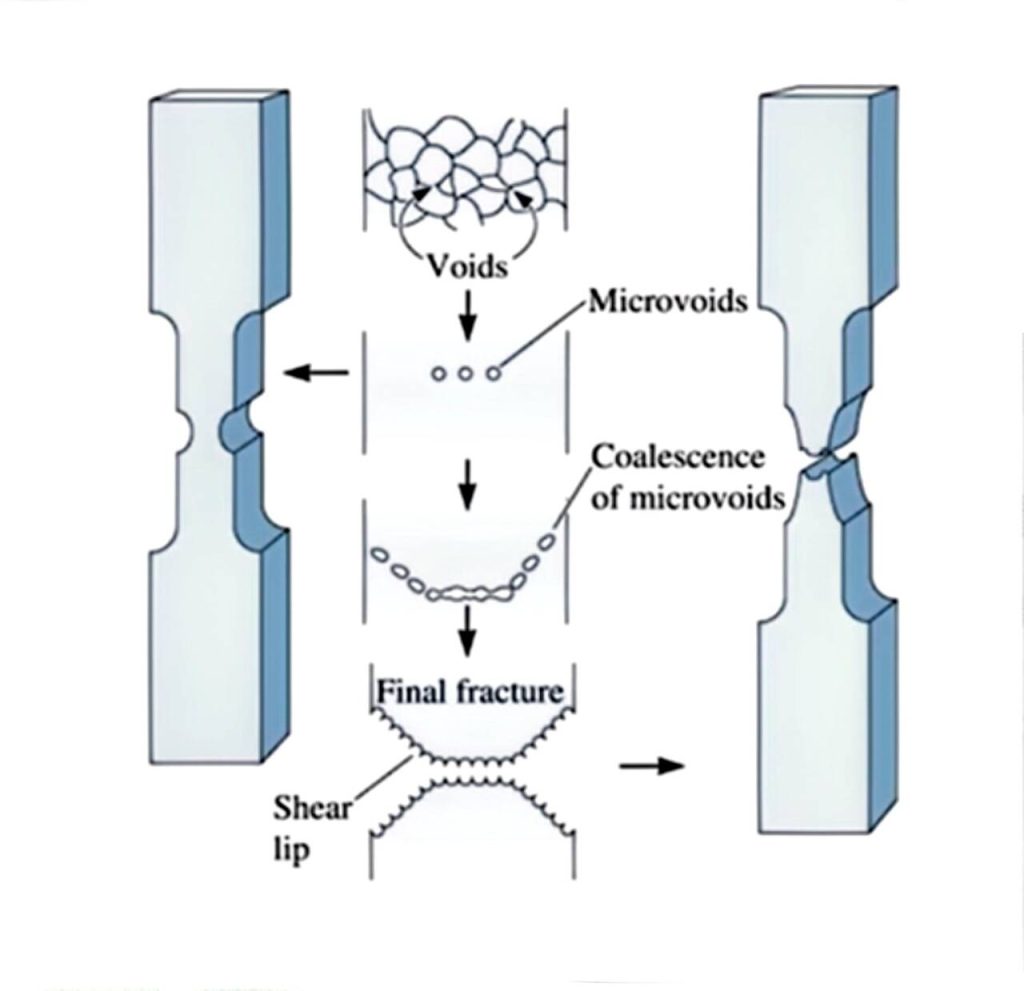
韧性失效的断裂过程

孔洞的形核，长大和聚合形成小裂纹，小裂纹长大形成大裂纹，直至失去承载能力.

脆性断裂

• 穿晶transgranular：裂纹穿过晶粒，没有明显的晶界
• 沿晶：平滑的晶界

穿晶和沿晶可能同时被观察到.

断口的形态 fractography

• 发生大量塑性变形（韧性）的断裂
• 发生少量塑性变形（脆性）的断裂

塑性变形的本质就是滑移，因而判断韧性/脆性变形，就是考虑是否有足够多的滑移.

一般而言，fcc和bcc比hcp有更好的塑性.
【BV14p4y1a7LL，25分钟左右】

裂纹的影响

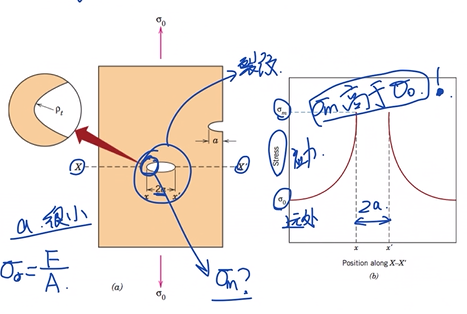
裂纹与应力集中 Stress concentration

$$
\sigma_m=2\sigma_0\left(\frac{a}{\rho_t}\right)^{\frac{1}{2}}
$$

该公式说明：裂纹前端的应力与所施加应力，与裂纹的状态有关.

• $\sigma_m$：裂纹前端的应力
• $a$：裂纹的长度

1. 裂纹在中间：$2a$
2. 裂纹在边缘：$a$

• $\sigma_0$：施加应力
• $\rho_t$：裂纹的弧度

其中，$a$远大于$\rho_t$.

断裂强度和裂纹的关系

格里菲斯公式：

$$
\sigma_c=\left(\frac{2E\gamma_s}{\pi a}\right)^\frac{1}{2}
$$

该公式说明断裂强度与裂纹大小之间的关系.

• $E$：杨氏模量（$GPa$）
• $\gamma_s$：表面能
  打开裂纹前端之间键合，而形成新表面所需要的能量.

断裂韧性 Fracture Toughness

考察材料对裂纹敏感性的参量.

$$
\sigma_c=\left(\frac{2E\gamma_s}{\pi a}\right)^{\frac{1}{2}}
$$

$$
K_c=Y\sigma_c\sqrt{\pi a}
$$

• $Y$是一个系数，代表不同裂纹状态（主要对应不同裂纹大小，即作为$a$的系数）

1. 裂纹在中间，$Y=1$
2. 裂纹在边缘，$Y\sim1.1$

$$
K_{Ic}=Y\sigma_c\sqrt{\pi a}
$$

$I$是罗马数字，代表不同施加应力的形式，此处代表opening式；可以替换成其它类型的施力形式.

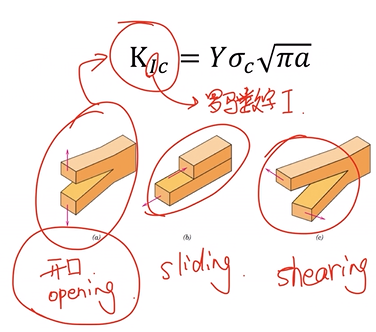
$\sigma_y$高，不代表材料有韧性，因为很小的裂纹就会导致断裂.

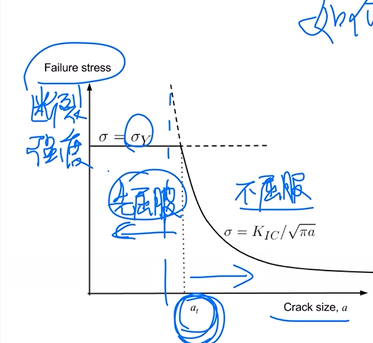
利用断裂强度来设计材料

---

Refrence

https://www.bilibili.com/video/BV14p4y1a7LL/?spm_id_from=333.1007.top_right_bar_window_history.content.click