本讲通过 close packing,polarisability,radius ratio 和 lattice energy 四个角度,解释不同AX₂化合物的结构差异,同时涉及结构推导、影响因素及热力学基础.
AX₂ Type Crystal Structures
AX₂结构均源于 face-centered cubic close packing (FCC/CCP) 或 hexagonal close packing (HCP),通过 interstices 形成,关键规则:
- FCC和HCP中,octahedral holes 数量 = 密堆积原子数
- FCC和HCP中,tetrahedral holes 数量 = 2×密堆积原子数
- 形成 AX₂ 化合物的两种方式:填充1/2八面体间隙,或填充全部四面体间隙
堆成 close packing 骨架的原子 / 离子,通常是 Anions(因为阴离子一般半径更大,先形成稳定的紧密结构,Cations 再填到间隙里;我们说的 “间隙数量”,都是基于这些 “密堆积原子” 的数量来算的;换言之,密堆积原子数是 “就是 一个 Close-Packing Unit Cell 中的原子 / 离子个数,即晶胞内实际占有的骨架原子数”.
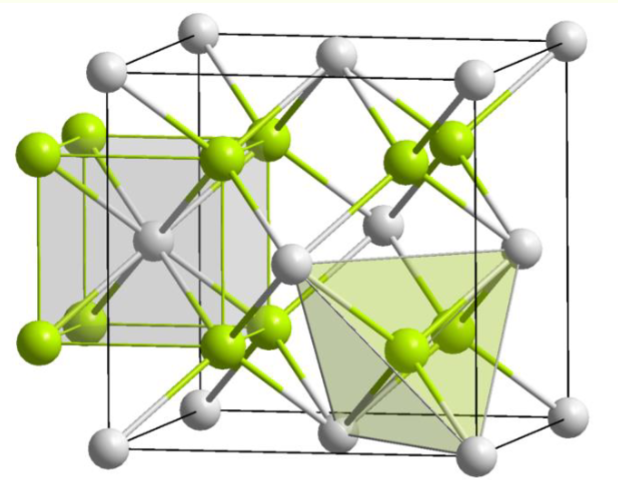
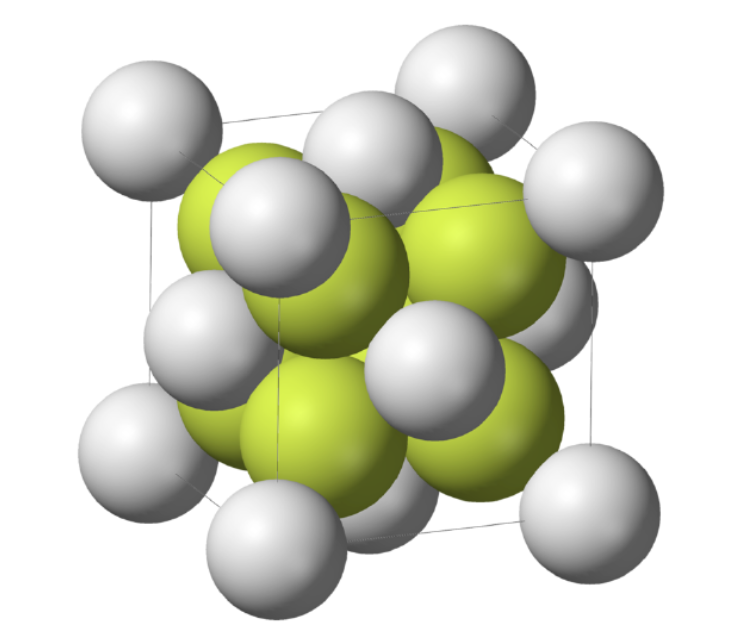
1. Fluorite Structure, CaF₂
- 堆积基元:阳离子(cation, Ca²⁺)形成 FCC close-packed lattice
- 间隙填充:填充全部四面体间隙(all tetrahedral holes),阴离子(anion, F⁻)占据间隙
- 离子半径:Ca²⁺(114 pm)、F⁻(119 pm),因阳离子较大,由阳离子构成密堆积(特殊点)
- 配位数(coordination number, CN):F⁻的配位数为4(四面体环境,tetrahedral environment),Ca²⁺的配位数为8(立方环境,cubic environment)
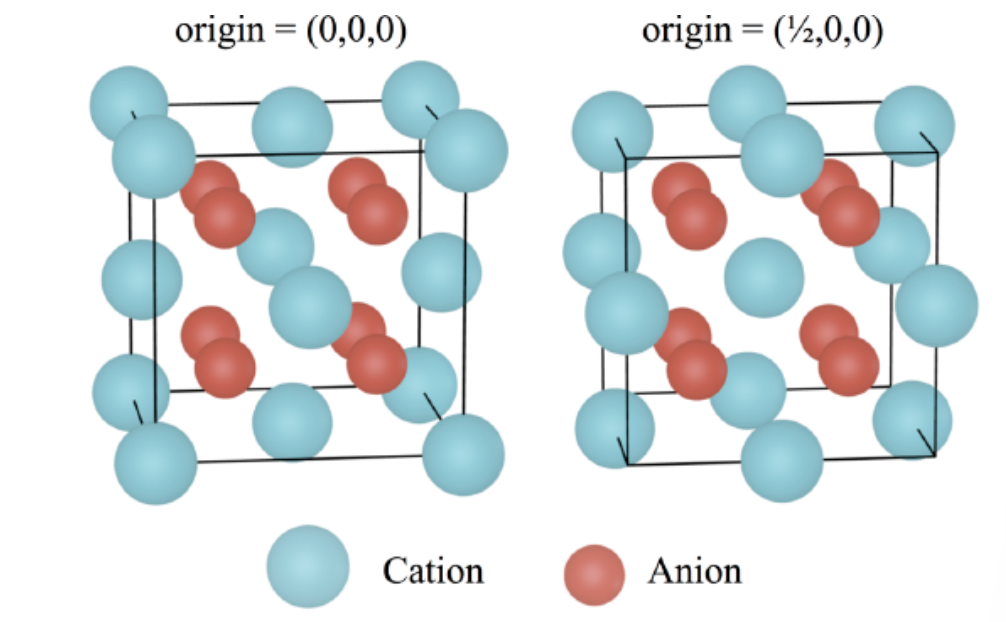
2. Anti-fluorite Structure, Na₂O
- 核心特点:与萤石结构完全相反,cations 和 anions 位置互换
- 堆积基元:阴离子(O²⁻)形成 FCC 密堆积晶格
- 间隙填充:填充全部四面体间隙,阳离子(Na⁺)占据间隙
- 离子半径:O²⁻(126 pm)、Na⁺(116 pm)
- 配位数:Na⁺的配位数为4(NaO₄多面体共边连接),O²⁻的配位数为8
Anti-fluorite Structure 是 AX₂ type ionic crystals 中更 “常规” 的结构,因为它遵循 ‘Anion 构成 close-packed framework,Cation 填充 interstices’ 的普遍规律;而 Fluorite Structure 是例外情况,仅因阳离子半径特殊才反向构成骨架.
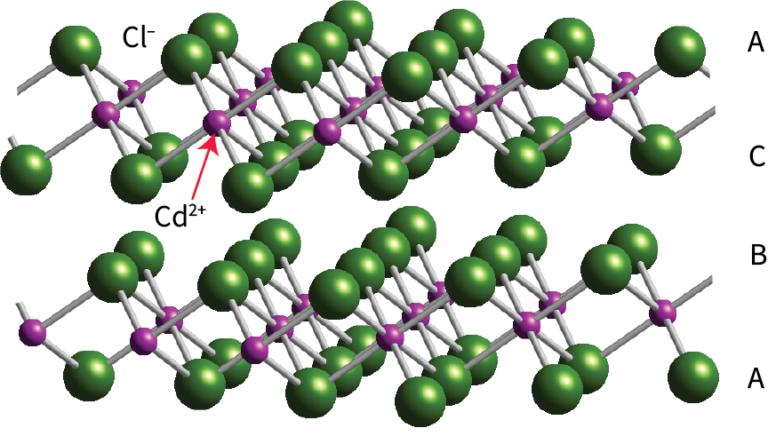
3. Cadmium Chloride Structure, CdCl₂
- 堆积基元:阴离子(Cl⁻)形成FCC密堆积晶格
- 间隙填充:填充1/2八面体间隙,Cd²⁺占据交替层(alternate layers) 的八面体间隙
- 结构特征:类似NaCl结构,但每层阳离子缺失一半(形成片状结构,sheet structure)
- 配位数:Cd²⁺ 的配位数为6(CdCl₆八面体,octahedra),Cl⁻的配位数为3
- 连接方式:CdCl₆ 八面体共边连接(edge-linked)
4. Cadmium Iodide Structure, CdI₂
- 堆积基元:阴离子(I⁻)形成HCP密堆积晶格
- 间隙填充:填充1/2八面体间隙,Cd²⁺占据交替层的八面体间隙
- 配位数:Cd²⁺的配位数为6(CdI₆八面体),I⁻的配位数为3
- 结构差异:与CdCl₂的堆积基元不同(FCC vs HCP),但均为二维片状结构(2D sheet structure)
关键疑问:为何HCP无“全四面体间隙填充”的 AX₂ 结构?
因会导致四面体共面连接(face-linking of tetrahedra),使多面体中心的离子距离过近,静电排斥(electrostatic repulsions)增大,结构不稳定.
Key Factors Influencing Ionic Structures
1. Electrostatics
- 核心原则:最大化阳离子-阴离子间的有利相互作用(favourable interactions),最小化阳离子-阳离子、阴离子-阴离子间的不利相互作用(unfavourable interactions)
- 本质:离子晶体结构的核心驱动力,决定离子的堆积方式和间隙填充优先级
2. Polarisability
- 定义:离子的 electron distribution 受其他离子影响而发生变形的倾向(tendency of electron cloud distortion)
- 核心公式:
$$\text{Polarisability} \approx \frac{r}{n}$$
其中,(r) = ionic radius,(n) = ionic charge - 规律:低电荷(low charge)、大半径(large radius)的离子极化率更高(更易变形)
- 对结构的影响:
- 阳离子与阴离子极化率相近:电子云无明显变形,形成三维网状结构(3D network structure)
- 极化率差异显著(阳离子极化能力强,阴离子易极化):阴离子电子云变形,电子密度向阳离子侧偏移,降低与其他阳离子的结合力,形成低维结构(2D片状如CdCl₂、CdI₂,或1D链状)
3. Steric Factors: Radius Ratio Rules
- 定义:通过阳离子半径(radius of cation, (r_C))与阴离子半径(radius of anion, (r_A))的比值,预测离子的配位数和晶体结构
- 核心公式:
$$\text{Radius Ratio} = \frac{\text{radius of small ion}}{\text{radius of large ion}} = \frac{r_{\text{小}}}{r_{\text{大}}}$$ - 关键规则:
- 通常阳离子更小(\(r_C < r_A\)),故半径比 = \(r_C / r_A\)
- 若阳离子更大(\(r_C > r_A\)),则半径比 = \(r_A / r_C\)(始终小于1)
- 半径比与结构的对应关系:
| Coordination Number, CN | Geometry | Radius Ratio Range | Typical Structure |
|---|---|---|---|
| 4 | Tetrahedral | 0.225 – 0.414 | Zinc Blende、Wurtzite |
| 6 | Octahedral | 0.414 – 0.732 | NaCl |
| 8 | Cubic | > 0.732 | CsCl、Fluorite |
- 几何推导核心公式(考试重点):
- Tetrahedral Coordination:
$$\sin\left(\frac{109.5^\circ}{2}\right) = \frac{r_A}{r_A + r_C} = 0.8166 \implies \frac{r_C}{r_A} = 0.225$$ - Octahedral Coordination:
$$\sin(45^\circ) = \frac{r_A}{r_A + r_C} = 0.707 \implies \frac{r_C}{r_A} = 0.414$$ - Cubic Coordination:
$$(r_A + r_C)^2 = 3r_A^2 \implies r_A + r_C = r_A\sqrt{3} \implies \frac{r_C}{r_A} = 0.732$$
- 局限性:半径比规则的预测准确率仅约50%,实际结构还受极化率、晶格能等影响(如NaCl结构比预测更常见)
Lattice Energy and Thermodynamics
Lattice Energy 不能直接测量,需通过两种方式获取:
- 实验测定:Born-Haber Cycle
- 理论计算:Born-Landé Equation
1. Definition of Lattice Energy
- 晶格能(Lattice Energy, (\Delta U)):0K时,1摩尔固态离子化合物由气态离子形成时的内能变化(change in internal energy)
- 反应式:
$$M^+(g) + nX^-(g) \to MX_n(s)$$ - 关键说明:晶格能不能直接测量(cannot be measured directly),需通过 Born-Haber Cycle 实验测定,或用 Born-Landé Equation 理论计算
Lattice Energy 的本质是离子间 Coulombic Attraction 的总体现,Lattice Energy 越负(数值越小),离子结合越牢固,化合物越稳定.
2. Difference Between Lattice Energy and Lattice Enthalpy
- 核心公式:
$$\Delta U = \Delta H – P\Delta V$$
其中,\(\Delta U\) = 晶格能(Lattice Energy),\(\Delta H\) = 晶格焓(Lattice Enthalpy),\(P\) = 压力(pressure),\(\Delta V\) = 体积变化(change in volume) - 近似关系:0K时的晶格能 \(\Delta U(0K) \approx 298K\) 时的晶格焓 \(\Delta_{\text{latt}}H(298K)\)(考试可近似等同使用)
3. Born-Haber Cycle for MCl
- 反应焓变公式(考试重点):
$$\Delta H_f(MCl, s) = \Delta H_{\text{atm}}(M) + I_1(M) + \frac{1}{2}\Delta H_{\text{bond}}(Cl-Cl) – E(Cl) + U(MCl, s)$$
其中:- \(\Delta H_f\) = 生成焓(enthalpy of formation)
- \(\Delta H_{\text{atm}}\) = 原子化焓(enthalpy of atomization)
- \(I_1\) = 第一电离能(first ionization energy)
- \(\Delta H_{\text{bond}}\) = 键解离能(bond dissociation energy)
- \(E\) = 电子亲和能(electron affinity)
- \(U\) = 晶格能(lattice energy)
固态氯化物(MCl)的生成反应是总反应:
$$\text{M (s)} + \frac{1}{2}\text{Cl}_2\text{ (g)} \rightarrow \text{MCl (s)} \quad \Delta H_f(\text{MCl, s})$$
但这个总反应无法直接通过实验测量焓变(反应条件复杂),因此通过Born-Haber 循环将其拆解为 5 个 “可测量 / 可计算” 的分步反应(每步对应公式中的一个项),根据 Hess 定律:总反应焓变 = 各分步反应焓变之和,最终得到公式:
$$\Delta H_f(\text{MCl, s}) = \Delta H_{atm}(\text{M}) + I_1(\text{M}) + \frac{1}{2}\Delta H_{bond}(\text{Cl-Cl}) – E(\text{Cl}) + U(\text{MCl, s})$$
化合物生成焓 = 金属原子化焓(破坏金属键)+ 第一电离能 + 氯气键解离能的一半 + 电子亲和能的负值 + 晶格能(离子结合成固体)
公式变形:
$$U = \Delta H_f – \Delta H_{atm} – I_1 – \frac{1}{2}\Delta H_{bond} + E$$
考试核心公式总结
(按考试高频度排序,可直接打印携带)
1. 极化率相关
$$\text{极化率(Polarisability)} \approx \frac{r}{n}$$
- 用途:判断离子变形能力,预测低维结构倾向
- 符号说明:(r) = 离子半径,(n) = 离子电荷
2. 半径比相关
$$\text{半径比(Radius Ratio)} = \frac{r_{\text{小}}}{r_{\text{大}}}$$
- 用途:预测配位数和晶体结构
- 关键补充:(r_{\text{小}}) 为较小离子半径(通常是阳离子),(r_{\text{大}}) 为较大离子半径(通常是阴离子)
3. 配位几何推导公式
- 四面体配位(coordination number = 4):
$$\frac{r_C}{r_A} = 0.225$$ - 八面体配位(coordination number = 6):
$$\frac{r_C}{r_A} = 0.414$$ - 立方体配位(coordination number = 8):
$$\frac{r_C}{r_A} = 0.732$$
4. 晶格能与焓的关系
$$\Delta U = \Delta H – P\Delta V$$
- 用途:近似换算晶格能和晶格焓(考试可近似 (\Delta U \approx \Delta H))
5. 玻恩-哈伯循环(MCl化合物)
$$\Delta H_f(MCl, s) = \Delta H_{\text{atm}}(M) + I_1(M) + \frac{1}{2}\Delta H_{\text{bond}}(Cl-Cl) – E(Cl) + U(MCl, s)$$
- 用途:计算晶格能或其他热力学参数
Exam Common Pitfalls
- 半径比的分子分母混淆:必须用“小离子半径/大离子半径”,而非固定“阳离子/阴离子”(若阳离子更大,需颠倒比值)
- 萤石与反萤石的堆积基元:萤石是阳离子(Ca²⁺)FCC堆积,反萤石是阴离子(O²⁻)FCC堆积,二者离子位置完全互换,配位数也互换
- 极化率的影响:仅当“阳离子极化能力强+阴离子易极化”时,才形成低维结构(2D/1D),而非所有极化率差异都导致低维结构
- 晶格能的定义:是“气态离子形成固态”的内能变化,而非反向过程(溶解或分解)
- 半径比规则的局限性:预测准确率仅50%,不能单独作为结构判断的唯一依据,需结合极化率和晶格能
- 配位数的定义:配位数是“周围紧邻的异号离子数”,如CaF₂中Ca²⁺的配位数是8(8个F⁻),F⁻的配位数是4(4个Ca²⁺),而非化学式比例2:1
- FCC与CCP的关系:面心立方最密堆积(FCC)与立方最密堆积(CCP)是同一结构,只是命名角度不同,间隙数量完全相同
0 条评论