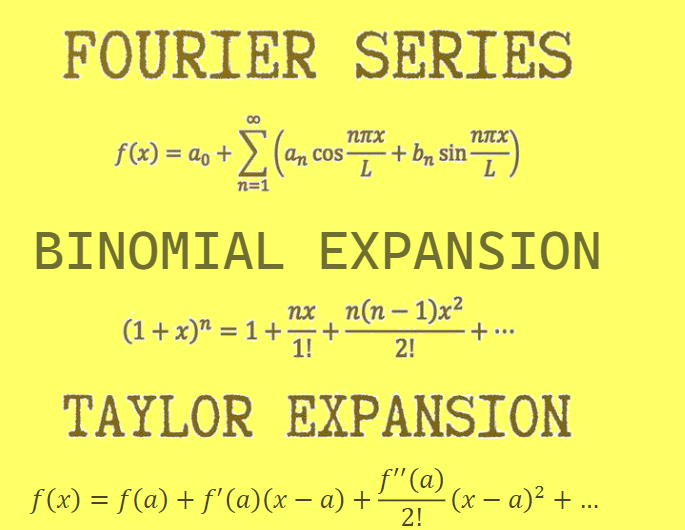
Fourier series is a method that can expand a complex periodic function into a sum of basic trigonometric functions (e.g., sine and cosine), and it is widely used to solve differential equations in real-world engineering applications.
Odd and Even Functions
奇偶函数的运算规则是简化傅里叶系数计算的关键.
Definition
- Even Function
对定义域内所有$x$,满足$f(−x)=f(x)$,symmetric about the y-axis.
示例:$f(x)=x^2$, $f(x)=cosx$(余弦函数), $f(x)=coshx$(双曲余弦函数)
- Odd Function
对定义域内所有$x$,满足$f(-x) = -f(x)$,symmetric about the origin
示例:$f(x)=x$, $f(x)=\sin x$(正弦函数), $f(x)=\tanh x$(双曲正切函数)
Properties of Odd and Even Functions
Sum
偶函数 + 偶函数 = 偶函数
奇函数 + 奇函数 = 奇函数
偶函数 ± 奇函数 = 既非奇也非偶(除非某一函数恒为 0)
Product
偶函数 × 偶函数 = 偶函数
奇函数 × 奇函数 = 偶函数
偶函数 × 奇函数 = 奇函数
偶函数 ÷ 偶函数 = 偶函数
奇函数 ÷ 奇函数 = 偶函数
偶函数 ÷ 奇函数 = 奇函数(分母≠0)
Derivative
偶函数的导数是奇函数(如$f(x)=x^2$的导数$f'(x)=2x$)
奇函数的导数是偶函数(如$f(x)=x$的导数$f'(x)=1$)
Composition
偶函数复合偶函数 = 偶函数(如$\cos(x^2)$)
奇函数复合奇函数 = 奇函数(如$\sin(x^3)$)
偶函数复合奇函数 = 偶函数(如$\cos(x^3)$)
Tips:关于Neither
- 当 neither 与odd或even函数 相乘 / 相除时,结果通常为 neither,但无绝对必然性;
- 当 neither 与另一个 neither 函数相乘时,可能得到odd或even,并不是任何情况均为 neither
- 最终结果需通过奇偶性定义验证,计算$f(-x)$与$f(x)$、$-f(x)$的关系,不能一概而论
Periodic Functions
Definition
若存在正数$T$(Period),对所有$x$满足$f(x+T)=f(x)$,则$f(x)$为周期函数.
Common Periodic Functions
| Function | Period | Amplitude | Note |
|---|---|---|---|
| \(\sin x\)、\(\cos x\) | \(2\pi\) | 1 (取值范围\([-1,1]\)) | 基本三角函数,傅里叶级数的 “基函数” |
| \(\tan x\) | \(\pi\) | 无(图像无界) | 正切函数的周期是\(\pi\),而非\(2\pi\) |
| \(\sin(nx)\)、\(\cos(nx)\) | \(\frac{2\pi}{n}\) | 1 | n为正整数,频率与n成正比(周期是\(\sin x\)的\(\frac{1}{n}\)) |
| \(\sin\left(\frac{n\pi x}{L}\right)\) | 2L | 1 | 全区间傅里叶级数的标准基函数,周期与区间长度L相关 |
Period-Frequency Relation
周期$T$与频率$f$(单位时间内重复次数)互为倒数:$f=\frac{1}{T}$
示例:$\sin(2x)$的周期$T=\pi$,频率是$\sin x$的 2 倍(每$\pi$重复一次)
Full Range Fouries Series
任何周期函数(无论形态复杂,如方波、锯齿波)都可表示为正弦函数($\sin$)和余弦函数($\cos$)的无穷叠加.
因此,可以将复杂函数分解为简单的 “基函数”,便于求解微分方程 .
Applicable Scenario
函数$f(x)$定义在对称区间$-L < x < L$ ,且周期为$2L$(即$f(x+2L)=f(x)$)
Series Formula
计算公式
$$f(x) = \frac{A_0}{2} + \sum_{n=1}^{\infty} \left[ A_n \cos\left(\frac{n\pi x}{L}\right) + B_n \sin\left(\frac{n\pi x}{L}\right) \right]$$
其中$n$为正整数($n = 1,2,3, \dots$)
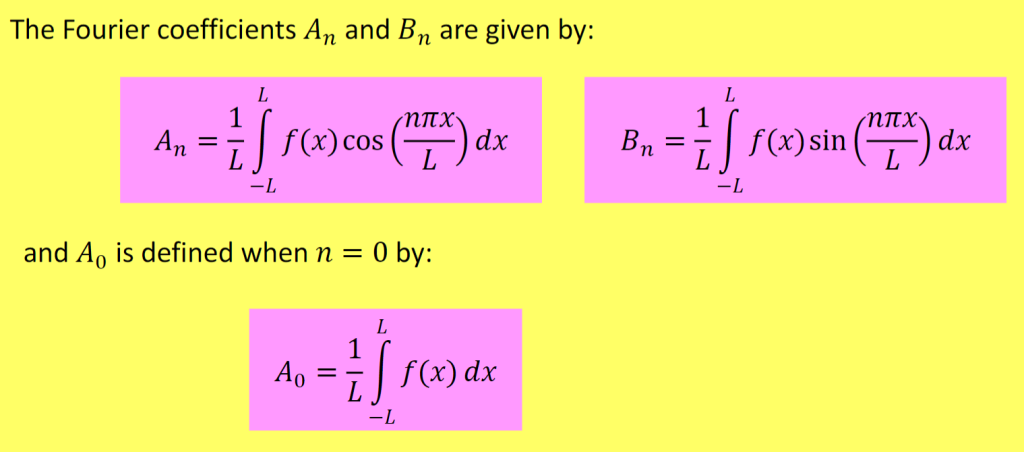
Harmonic Number
在傅里叶级数中,n是正整数变量,用于标记级数中不同频率的正弦和余弦项。
对于项$A_n \cos\left( \frac{n\pi x}{L} \right)$和$B_n \sin\left( \frac{n\pi x}{L} \right)$,$n$越大,三角函数的 “振荡频率” 越高(比如$n=1$是基波,$n=2$是二次谐波,以此类推)
相关疑问
- 疑问 A:为什么没有\(B_0\)?
根据正弦项系数\(B_n\)的定义 \(B_n = \frac{1}{L}\int_{-L}^{L} f(x)\sin\left( \frac{n\pi x}{L} \right)dx\),当\(n=0\)时,\(\sin(0)=0\),因此:
$$B_0 = \frac{1}{L}\int_{-L}^{L} f(x)\cdot 0 \, dx = 0$$
即\(B_0\)恒为 0,所以级数中无需单独列出\(B_0\)项
- 疑问 B:为什么\(A_0\)要除以 2?
傅里叶级数本质上可定义在所有整数n(\(-\infty < n < \infty\)),但若仅取正整数\(n \geq 1\),需对\(A_n\)、\(B_n\)的系数进行 “加倍补偿”
但\(A_0\)没有正负配对(无\(n=\pm0\)),因此为保持系数一致性,需将\(A_0\)除以 2
Half-Range Fourier Series
当函数仅在Half Interval上定义,如 $0<x<L$,而非完整的对称区间时,我们需要将其扩展为周期为 $2L$ 的Periodic Function,再展开为Fourier Series;
这种仅基于半区间定义、通过扩展得到的傅里叶级数,称为Half Range Fourier Series.
Two Extension Methods
根据边界条件选择扩展方式,核心是 “仅保留正弦或余弦项,简化计算”:
| Extension Type | 适用边界条件 | Series Form | Coefficient Formula |
|---|---|---|---|
| Odd Extension | $f(0)=0$ 如杆的一端固定,位移为 0 | 仅含正弦项: $f(x)=\sum_{n=1}^{\infty} b_n$ $\sin\left(\frac{n\pi x}{L}\right)$ | $b_n = \frac{2}{L} \int_{0}^{L} f(x) \sin\left(\frac{n\pi x}{L}\right) dx$ |
| Even Extension | $f'(0)=0$ 如杆一端无热流,温度梯度为 0 | 仅含余弦项: $f(x)=\frac{a_0}{2} +$ $ \sum_{n=1}^{\infty} a_n \cos\left(\frac{n\pi x}{L}\right)$ | $a_0 = \frac{2}{L} \int_{0}^{L} f(x) dx$ $a_n = \frac{2}{L} \int_{0}^{L} f(x) \cos\left(\frac{n\pi x}{L}\right) dx$ |
考试和工程应用中,需根据boundary conditions选择扩展方式.
Odd Extension
奇函数满足 \(f(0)=0\)(因 \(f(-0) = -f(0) \implies f(0)=0\)),且Fourier series仅含正弦项,计算更简洁
Even Extension
原函数 \(f(x)=x^2\) 在 \(x=0\) 处的导数 \(f'(0)=0\),Even Extension后函数的导数是Odd function(这是规律,Even的导数为Odd),故 \(f'(0)=0\)(奇函数在 \(x=0\) 处值为 0);此时Fourier Series仅含余弦项,计算更简洁
公式总结
Fourier 奇偶函数简化技巧
$$f(x) = \frac{A_0}{2} + \sum_{n=1}^{\infty} \left[ A_n \cos\left(\frac{n\pi x}{L}\right) + B_n \sin\left(\frac{n\pi x}{L}\right) \right]$$
| 函数类型 | 系数简化结果 | 级数形式 |
|---|---|---|
| Even | \(B_n = 0\);\(A_0 = \frac{2}{L}\int_{0}^{L}f(x)dx\);\(A_n = \frac{2}{L}\int_{0}^{L}f(x)\cos\left(\frac{n\pi x}{L}\right)dx\) | 仅含常数项 + 余弦项 |
| Odd | \(A_0 = 0\),\(A_n = 0\);\(B_n = \frac{2}{L}\int_{0}^{L}f(x)\sin\left(\frac{n\pi x}{L}\right)dx\) | 仅含正弦项 |
| Neither | 无简化,需计算所有系数 |
Useful Integrals Involving Trigonometric Functions
http://www.adso2004.top/index.php/2024/11/08/cmc2024/ 分部积分等初等数学技巧
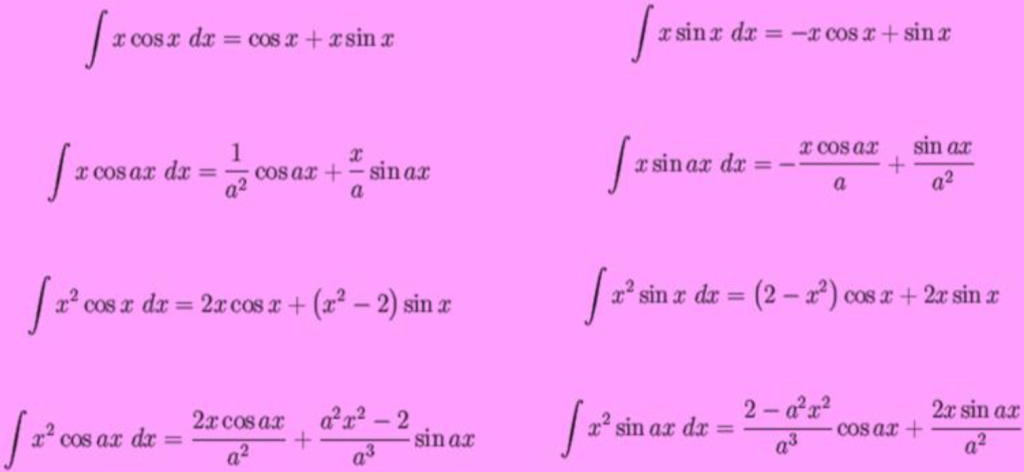
$\begin{align*} \int x\sin x dx &= -x\cos x + \sin x + C \\ \int x\sin(ax) dx &= -\frac{x\cos(ax)}{a} + \frac{\sin(ax)}{a^2} + C \quad (a\neq0) \\ \int x^2\sin x dx &= (2 – x^2)\cos x + 2x\sin x + C \\ \int x\cos x dx &= x\sin x + \cos x + C \\ \int x\cos(ax) dx &= \frac{x\sin(ax)}{a} + \frac{\cos(ax)}{a^2} + C \quad (a\neq0) \end{align*}$
三角函数取值规律
$\sin(n\pi) = 0$(对所有整数n,Integer n)
$\cos(n\pi)=(-1)^n$(对所有整数n,Integer n)
0 条评论