目录
晶向指数与晶面指数
晶向指数$[u\ v\ w]$消分母的原因
定原点 – 建坐标 – 定终点 – 连直线
- 反映方向向量的比例关系 晶向指数描述的是晶体中某一方向的向量。向量的本质是方向，其分量比例决定方向。例如，向量坐标为 \((\frac{1}{2}, \frac{1}{3}, 0)\)，消分母（同乘 6）得到 \([320]\)，仅需保留分量的整数比例，即可唯一确定方向，无需额外处理.
- 简化方向标识 消分母将分数化为最简整数比，使晶向指数更简洁直观。无论原始分量是分数还是整数，消分母后均以整数比形式呈现（如 \([111]\)、\([123]\)），方便对比和记忆不同晶向的方向特征.
晶面指数取倒数的原因
定原点 – 建坐标 – 取倒数 – 化简（取公约数） – 连线
- 统一描述晶面相对位置 晶面可能与晶轴相交于不同截距（包括无穷大），直接使用截距无法有效区分晶面方位。例如，截距为 2、3、6 的晶面和截距为 1、\(1.5\)、3 的晶面，实际是平行晶面。取倒数后，两者倒数均为 \(\frac{1}{2}:\frac{1}{3}:\frac{1}{6}=3:2:1\)，能消除截距数值差异，统一描述平行晶面的相同方位.
- 突出晶面与晶轴的 “疏密关系” 截距小，说明晶面离原点近，与该晶轴方向原子排列更 “紧密”。取倒数后，数值越大代表晶面在对应晶轴方向上与原子排列的 “关联更密切”，例如截距为 1（倒数为 1）比截距为 2（倒数为 \(0.5\)）的晶面，在该轴方向与原子排列的关系更紧密.
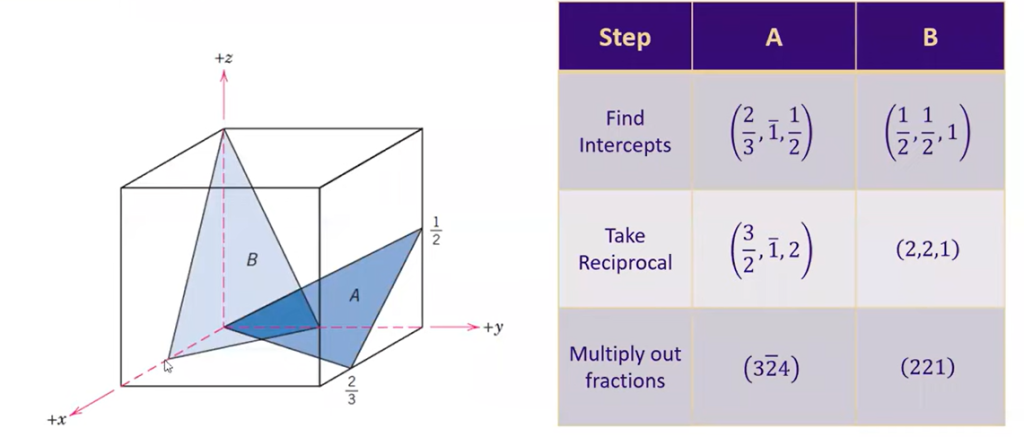
确认晶面的原点，似乎是距离晶面最近且不在晶面上的点.
我操这几个我一个都不会：
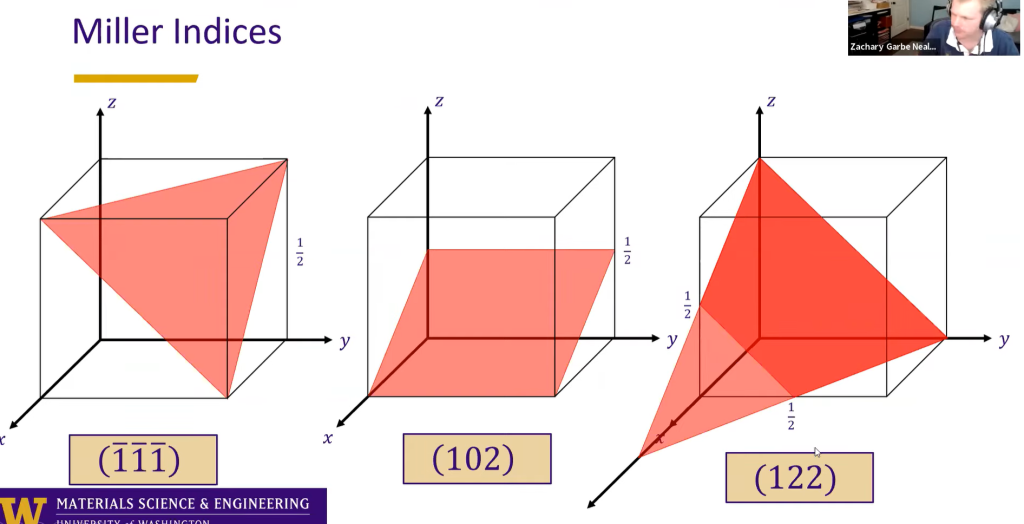
简言之，晶面指数通过取倒数消除截距差异、统一方位描述；晶向指数通过消分母保留方向向量的比例关系，二者服务于不同的晶体学描述目标.
四坐标轴
除了用三轴坐标下的晶面指数 $(hkl)$ 外，还可通过变换坐标轴，采用四轴坐标系统下的 $(h k i l)$ 表示晶面指数.
配位数与最密排面
找到SC，FCC，BCC，HCP几种晶体的原子配位方式，就可轻易得到其空间利用率和最密排面.
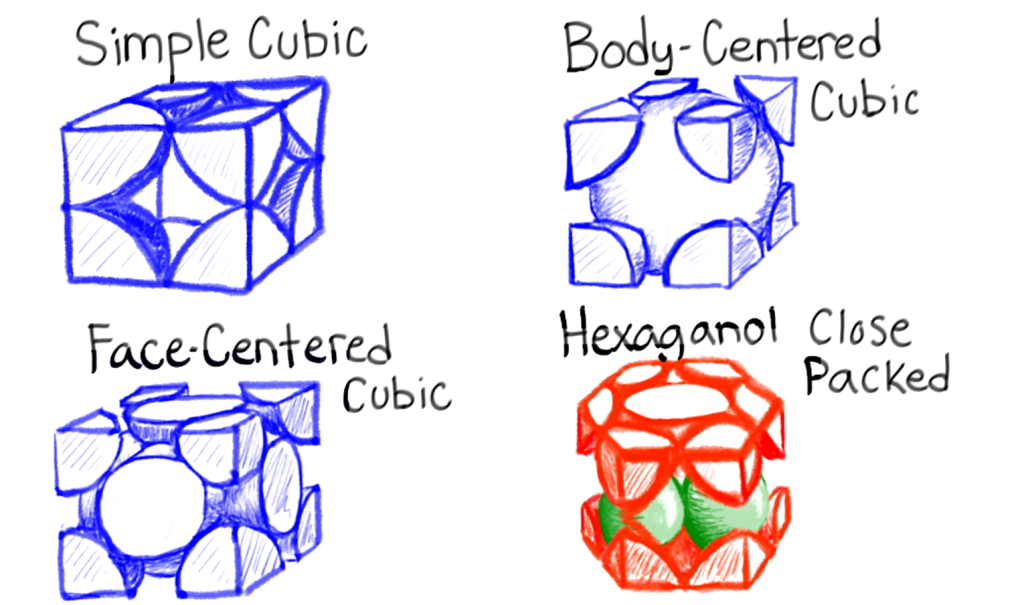
Simple Cubic
每两个球在棱上相切，$$a=2R$$
配位数=6
Body centered cubic
在体对角线上两两相切，棱上的球间有未知大小的空隙
$$4R=\sqrt{3}a$$
选择体心为参照，配位数=8
Face centered cubic
面对角线上相切
$$4R=\sqrt{a}$$
配位数=12
Hexagonal close packed
此前有一篇文章介绍这种结构：http://www.adso2004.top/index.php/2024/10/21/hexagonal-close-packed-crystal-structure-hcp/
https://en.wikipedia.org/wiki/Close-packing_of_equal_spheres
配位数=12
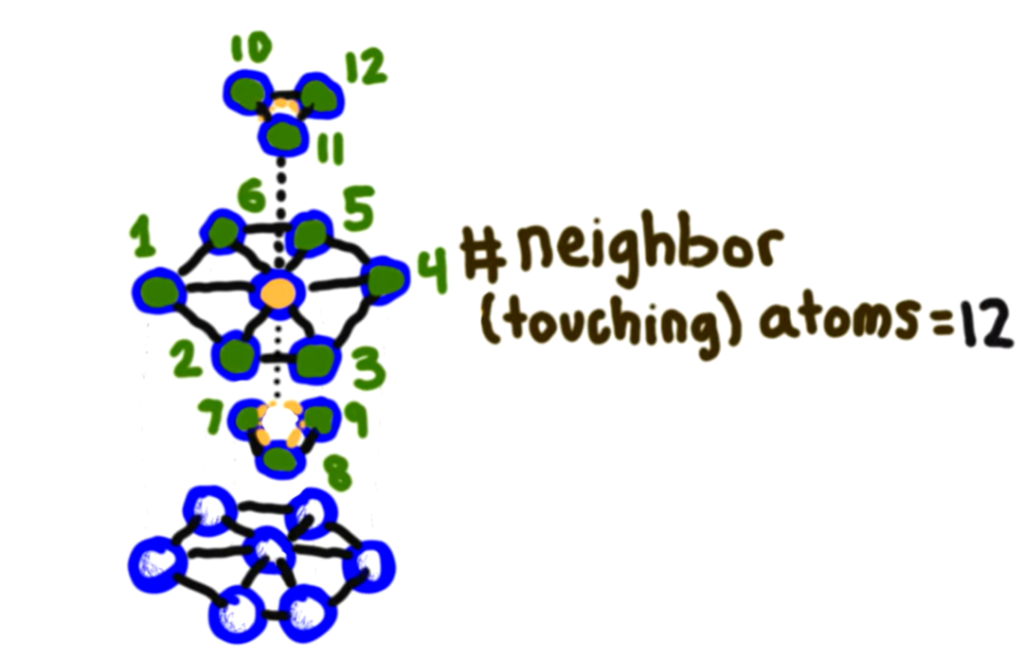
FCC和HCP来源于相同的初始堆叠
0 条评论