热力学是研究热力学过程中热与功的转化关系与条件的.

理想气体的每一个平衡态，都可以用$p-V$图上的一个点来表示；而简单系统的准静态过程，则可以用$p-V$图上的一条曲线表示.

基本概念

内能$E$：状态量

$$E=\frac{M}{\mu}\frac{i}{2}RT$$

气体系统内部所具有的能量，是状态量（即只与气体所处的状态有关）

功$A$：过程量

$$A=\int_{V1}^{V2}pdV$$

气体从一种状态$(V_1,p_1)$到另一种状态$(V_2,p_2)$，系统对外所做的功（有正负之分）

热量$Q$：过程量

$$Q=\frac{M}{\mu}C_m(T_2-T_1)$$

气体系统与外界之间，由于有温差 而传递的能量.
其中$C_m$为摩尔热容，即1$\text{mol}$的某种物质升高（或降低）$1\text K$所需要吸收（或放出）的热量，单位$\text J/(mol\cdot K)$

• 同种物质在同样温度下的摩尔热容，随过程不同而变化
  同温度下，若要使气体保持压强不变而升高$1\text K$，所吸收的热量要比使其保持体积不变而升高$1\text K$要多，因为等压升温要求体积变大，要对外做功.
• 同种物质在同过程中的摩尔热容，随温度的不同而变化
  一般近似认为摩尔热容是关于温度的常数

热力学基本定理

热力学第一定律

$$Q=\Delta E+A$$
系统从外界吸收的热量，一部分增加了气体的内能，一部分用于对外做功

• $Q+$：系统从外界吸热；$Q-$：系统向外界放热
• $E+$：系统的内能增加，温度升高；$E-$：系统的内能减少，温度降低
• $A+$：系统对外做功（做正功）；$A-$：外界对系统做功（做负功）

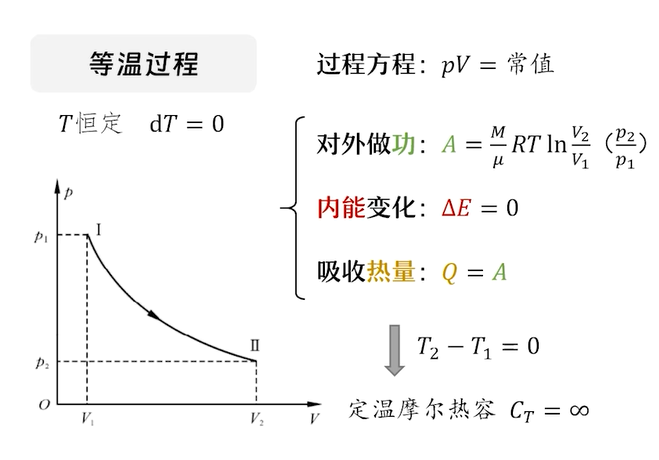
三种等值过程

摩尔热容是根据热力学第一定律的公式$Q=\Delta E+A$列出的三个方程，而进一步求解得到的.

• 比热容比

$$\lambda=\frac{C_p}{C_v}=\frac{2+i}{i}$$

• 迈耶公式

$$C_p=C_v+R$$

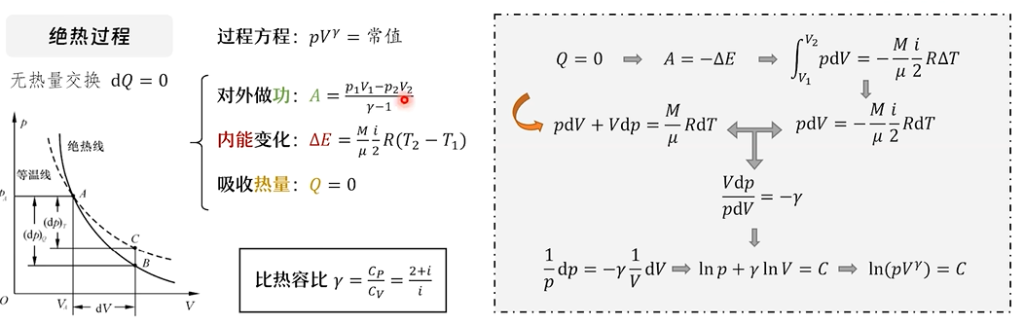
绝热过程与多方过程

热传递

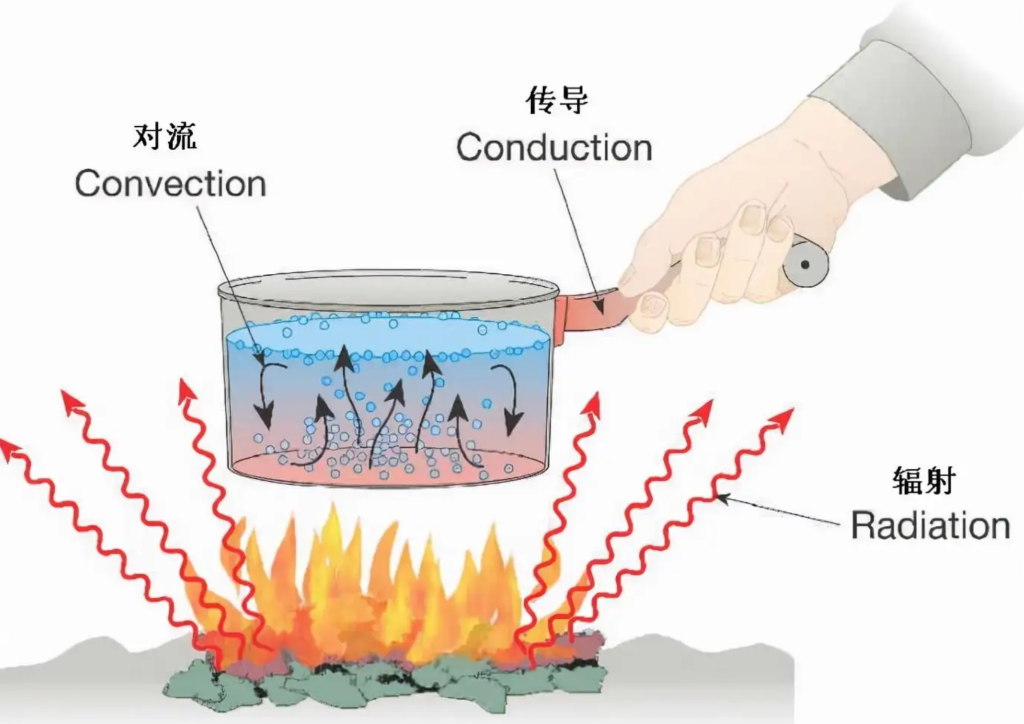
导热基本定律 Fourie’s law of heat conduction

$$
q=-\lambda\frac{\partial T}{\partial x}
$$
$$
\vec{q}=-\lambda\frac{\partial T}{\partial n}\vec{n}=-\lambda\nabla T
$$
负号代表热量传递方向与温度升高的方向相反.

热传导 Fouriw’s law

$$ \Phi =-\lambda A\frac{T_1-T_2}{L} $$
其中$\Phi$为热流量

热辐射 Stefan-Boltzmann

$$E=\sigma T^4$$
其中，$E$是单位时间上辐射的总能量，$T$是黑体的绝对温度，$\sigma=5.67\times 10^{-8}W/m^2\cdot K^4$是斯蒂藩-玻耳兹曼常数.
斯蒂藩-玻耳兹曼定律表明$E\propto T^4$，即物体的温度越高，辐射的总能量就越大.