
核外电子的运动的特殊性
波粒二象性
\begin{cases}
E=mc^2\\
E=h\nu
\end{cases}
$\Rightarrow mc^2=h\nu \Rightarrow mc^2=h\frac{c}{\lambda}$ ,又由$p=mc$,
\begin{aligned} \Rightarrow \lambda=\frac{h}{p} \end{aligned}
具有动量$p$的微观粒子,其物质波波长为$\lambda$.
单个粒子呈现粒子性;而波动性是粒子性的统计结果.
Schodinger方程与波函数
波函数的引入
为研究电子出现的空间区域,通过函数图像和空间区域建立联系,该函数记作$\psi$,即波函数.
$$ \frac{\partial^2 \psi}{\partial x^2}+\frac{\partial^2 \psi}{\partial y^2}+\frac{\partial^2 \psi}{\partial z^2}+\frac{8\pi^2m}{h^2}(E-V)\psi=0 $$
由薛定谔方程求解而得的描述电子运动状态的波函数,在量子力学上叫作原子轨道;原子轨道可以表示核外电子的运动状态,它与经典的轨道含义不同,是一种轨道函数,有时称轨函.
Schodinger方程的求解
已知条件:
- 电子质量$m$
- 核外电子势能$V$
偏微分方程的解是一组多变量函数,如$F(x,y,z)$;波函数$\psi$即一系列多变量函数,经常是关于三个变量.
解:
核外电子处于原子核的球形电场中,将核外电子的势能$V=-\frac{Ze^2}{r}$,其中$e$为元电荷电子的电量,$Z$是原子序数,$r$是电子与核的距离;将该式代入薛定谔方程.
- 波函数$\psi$
- 电子能量$E$
解出每一个原子轨道,都同时解得一个特定的能量$E$与之相对应.
对于氢原子来说,$E=-13.6eV\times\frac{1}{n^2}$,式中$n$是参数,$eV$是能量单位.
- 引入球坐标
由于情形是球形电场,所以将三维直角坐标系变换成球坐标系,从而将问题简化.
$$ F(x,y,z)\Rightarrow F'(r,\theta,\varphi) $$
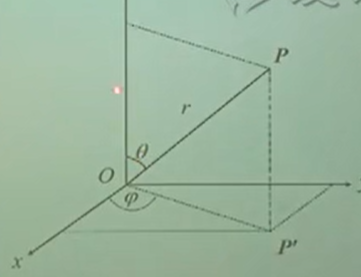
- $\theta$:$OP$与$z$轴的夹角,$\theta \in[0,2\pi]$
- $\varphi$:$OP$与$x$轴的夹角,$\theta \in[0,2\pi]$
$$ \Rightarrow \begin{cases} &x=r\sin\theta\cos\varphi \\ &y=r\sin\theta\sin\varphi\\ &z=r\cos\theta \end{cases} ,\ \ r^2=x^2+y^2+z^2$$

- 变量分离
将含有三个变量的偏微分方程,分解为三个单变量的常微分方程:
$$\psi(r,\theta,\varphi)=R(r)\cdot \Theta(\theta)\cdot\Phi(\varphi)$$
令$Y(\theta,\varphi)=\Theta(\theta)\cdot \Phi(\varphi)$,观察到$Y(\theta,\varphi)$仅与$\theta,\varphi$有关,称为 波函数的角度部分.
由此可见,波函数表示为两部分的乘积,即径向部分$R$和角度部分$Y$.

- 求特解
在解常微分方程时,引入三个参数$n,l,m$,仅当这三个参量满足特定要求时,所得波函数$\varphi$才是合理的解.

核外电子运动的描述
四个量子数
主量子数$n$
- 取值
取值为正整数,$1,2,3,4,\cdots$
光谱学上用$K,L,M,N\cdots$表示
- 意义
表示核外电子离核的远近,或者电子所在的电子层数.
- 能量计算
$$ E=-13.6eV\times \frac{Z^2}{n^2} $$
由此可计算每个电子层上电子的能量.
特别地,$n\rightarrow \infty, E=0$;即自由电子,其能量最大,为0.
由于$n$的取值是正整数,因此能量只有不连续的几种取值,即能量是量子化的,故$n$称为量子数.
- 多电子体系
对于单电子体系,其能量完全由$n$决定;但是多电子体系的能量,同时要受到其它量子数的影响,不完全取决于$n$,而且和$l$有关.
角量子数$l$
- 取值
角量子数$l$的取值受到主量子数$n$的限制;对于确定的主量子数$n$,角量子数$l$可以为$0,1,2,3,4,\cdots,(n-1)$,共$n$个取值.
光谱学上依次用$s,p,d,f,g,\cdots$表示.
- 意义
角量子数$l$决定原子轨道的形状:
$l=0,s$轨道:球形
$l=1,p$轨道:哑铃形
$l=2,d$轨道:花瓣形
- 能量计算
电子绕核运动时,不仅具有能量,而且具有角动量$\vec{M}$;角动量的模$|\vec{M}|$由角量子数$l$决定.
$$|\vec{M}|=\sqrt{l(l+1)}\frac{h}{2\pi}$$
故角动量的大小也是量子化的.

电子核外排布与元素周期律
多电子原子的能级 The energy level of a multi-electron atom
屏蔽效应 Shielding effect
- 有效核电荷和多电子体系的近似能量公式 Effective nuclear charges & Approximate energy formulas for multi-electron systems
核外电子中和质子,而中和后的核电荷$Z$即为有效核电荷$Z^{*}$,由此可将多电子体系简化为单电子体系.
$$Z^{*}=Z-\sigma$$
其中$sigma$为屏蔽常数(shielding constant);$\sigma$越大,表示核电荷被中和掉的越多.
模拟单电子体系的能量公式$ E=-13.6eV\times \frac{Z^2}{n^2} $ 得到多电子体系的近似能量公式:
$$ E=-13.6eV\times \frac{Z^{*2}}{n^2} =-13.6eV\times \frac{(Z-\sigma)^2}{n^2}$$
- 屏蔽效应 Shielding effect
在多电子体系中,核外电子抵消(中和)部分核电荷,使被讨论的电子受到的核的引力变小,这种作用称为其它电子对被讨论的电子的屏蔽效应;受到屏蔽作用的大小,因电子的角量子数$l$的不同而不同.
- 能级分裂 Energy level splitting

钻穿效应 Drill-through effect
用以解释屏蔽效应,角量子数$l$不同的电子受到的屏蔽作用之所以不同,其原因要归结于$l$不同的轨道径向分布的不同.
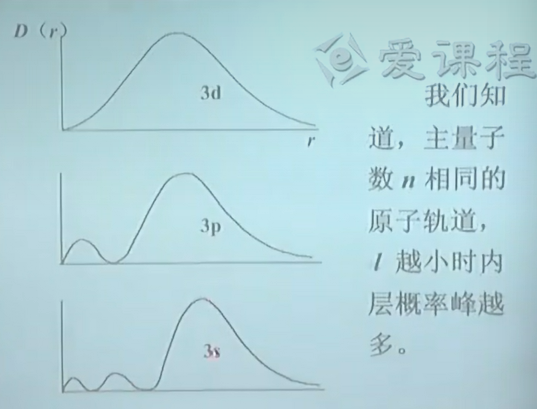
电子在内层出现的概率大,则受到的屏蔽小,即电子离核近,故能量低.
由于径向分布的不同,$l$不同的电子钻穿到核附近回避其它电子屏蔽能力不同,从而使自身的能量不同.
- 能级交错现象 The nucleus staggering phenomenon

原子轨道近似能级图
所有的原子轨道,共分成七个能级组
第七组 $7s$ $5f$ $6d$ $7p$
第六组 $6s$ $4f$ $5d$ $6p$
第五组 $5s$ $4d$ $5p$
第四组 $4s$ $3d$ $4p$
第三组 $3s$ $3p$
第二组 $2s$ $2p$
第一组 $1s$
各能级组中,能量由高到底依次为:$ns,(n-2)f,(n-1)d,np$.
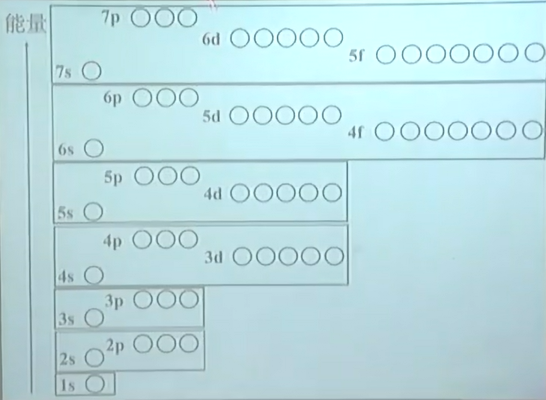
组间能级间能量差小,能级组间能量差大.
杂化轨道理论 Hybrid orbital theory
杂化轨道理论并非是用以判断构型的,而是用以解释构型的,即解释已知分子构型的成键形式等.
杂化概念 Hybridization
在形成原子分子的过程中,中心原子的若干能量相近的的原子轨道重新组合,形成一组新的原子轨道;这个过程叫作轨道的杂化,产生的新轨道叫作杂化轨道.
新形成的杂化轨道(如$sp^3$),既不同于$s$轨道,也不同于$p$轨道;杂化轨道有自己的波函数、能量、形状和空间取向.
杂化轨道的数目、形状、成分和能量
杂化过程中形成的杂化轨道的数目,等于参加杂化的轨道的数.(轨道数守恒)
$s-p$型杂化
$sp^{1}$杂化
- Linear structure of beryllium dichloride

$C$激发填充p轨道,其中1个s轨道和1个$p$杂化得到2个$sp$杂化轨道,这两条$sp$杂化轨道互相成180°夹角.
- Linear structure of acetylene molecule

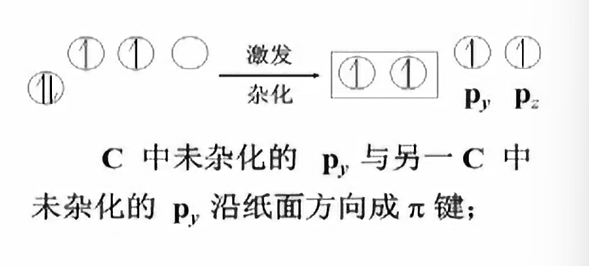
首先由$\sigma$键决定分子构型.
- Linear structure of the carbon dioxide molecule

然后。没有参与杂化的轨道形成$\pi$键.
- 两点结论
- 分子构型由$\sigma$键确定
- $\pi$键在$\sigma$键的基础上形成
$sp^{2}$杂化
- Boron trichloride

- Ethylene molecules
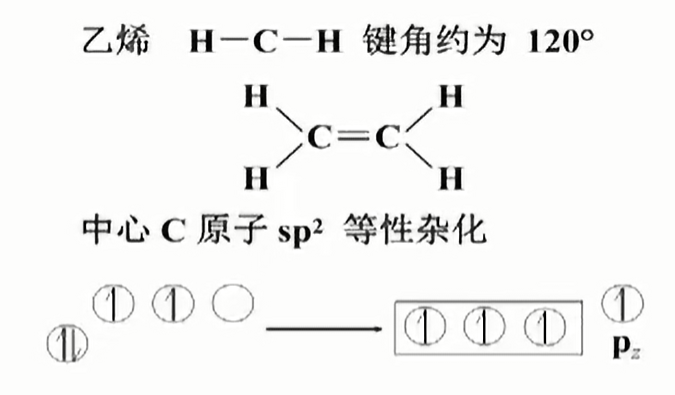
激发;1个$s$轨道、两个$p$参与杂化,从而形成两个$sp^2$杂化轨道.
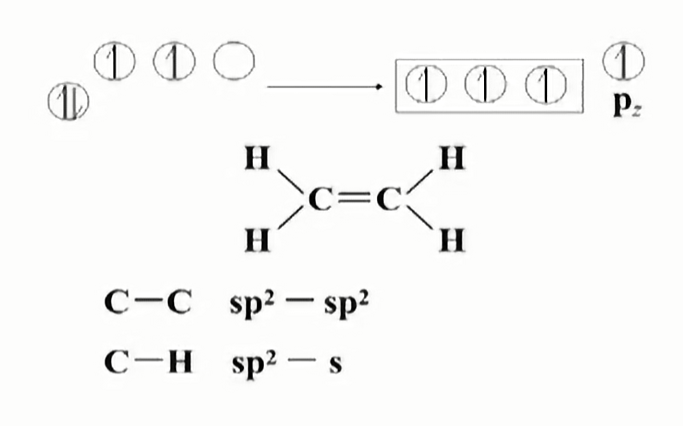
两个$C$原子的杂化轨道成键
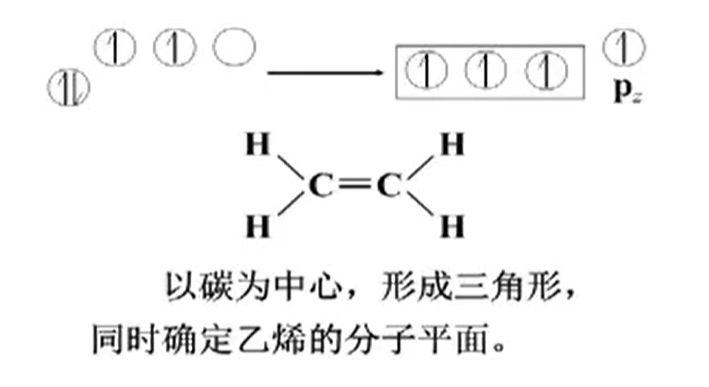
由此可得$H-C-H$键角为120°.
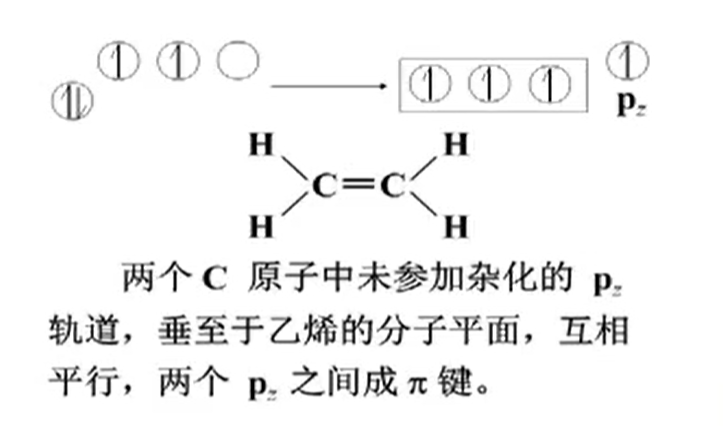
同时垂直于纸面的$p_z$轨道可以发生重叠,从而形成$\pi$键.
- Benzene与$\Pi_{6}^{6}$的引入

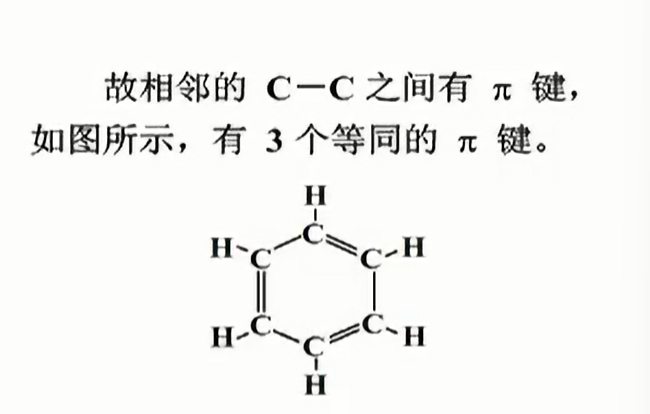
这样的解释是有问题的.
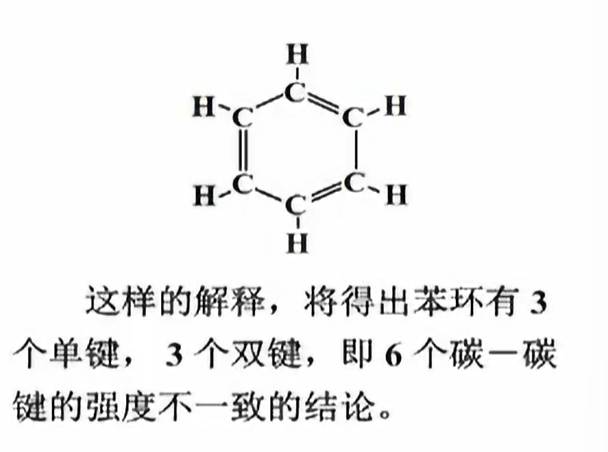
这与实验测试结果不符合;测试结果表明,苯环中不仅6个$C$等同,6个$H$等同,而且6个$C-C$键等同.
事实上,6条$p_z$轨道对称性一致,互相重叠,可以认为形成大$\pi$键,记作$\Pi_{6}^{6}$;
$\Pi_{6}^{6}$称为6中心6电子键,也称作不定域$\pi$键,或离域$\pi$键,
$sp^{3}$杂化
- methane
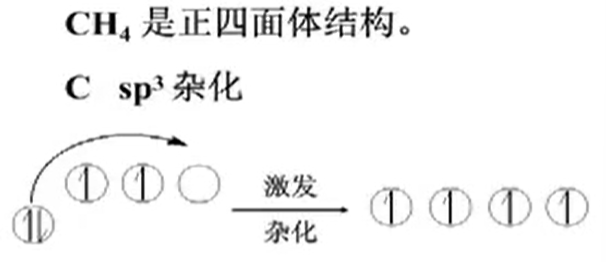
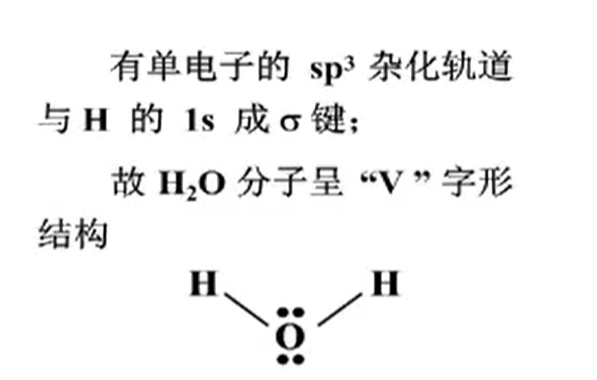
4条$sp^{3}$杂化轨道呈正四面体分布,分别与4个$H$的$1s$成$\sigma$键.
故而$CH_4$中没有未参与杂化的轨道,则无双键.
$s-p-d$型杂化
$s-p-d$杂化
- phosphorus pentachloride
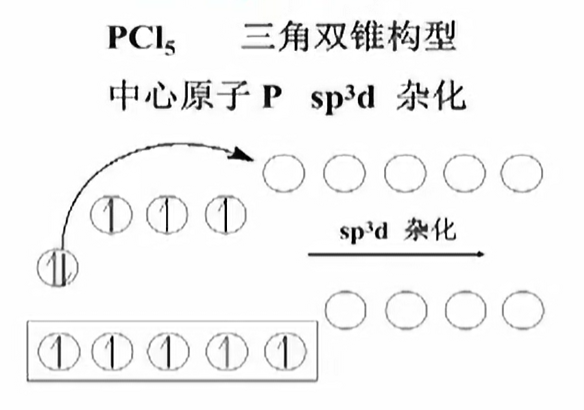
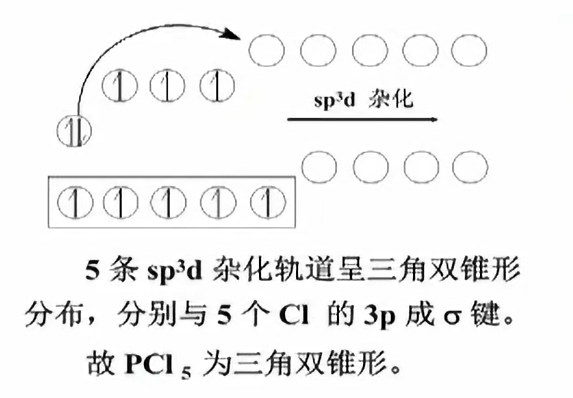
$s-p-d^2$杂化
- Selenium hexafluoride
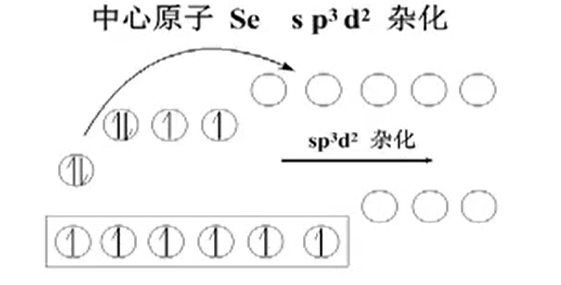
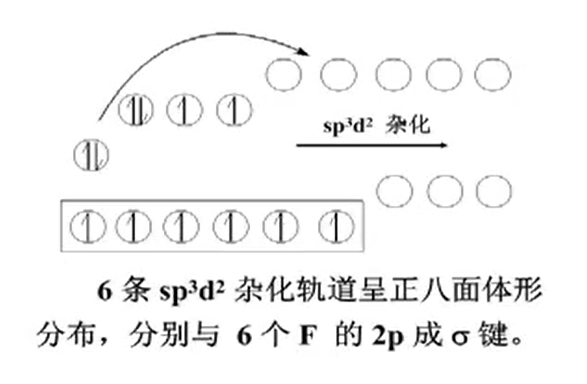
以上按参与杂化的轨道类型进行分类,将杂化轨道分为$s-p$杂化轨道和$s-p-d$杂化轨道;还可以按照能量关系进行分类.
杂化轨道能量关系

等性杂化
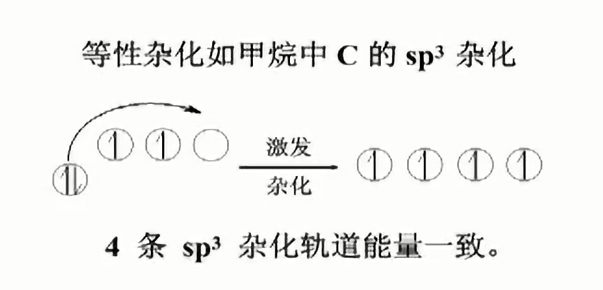

判断是否是等性杂化,要看各条杂化轨道的能量是否相等,而不需要考虑未参与杂化的轨道的能量.

如$CH_3Cl$,严格来讲其杂化也应属于不等性杂化.
换言之,杂化轨道还要考虑与配体成键后的轨道能量情况,但在此基本忽略.
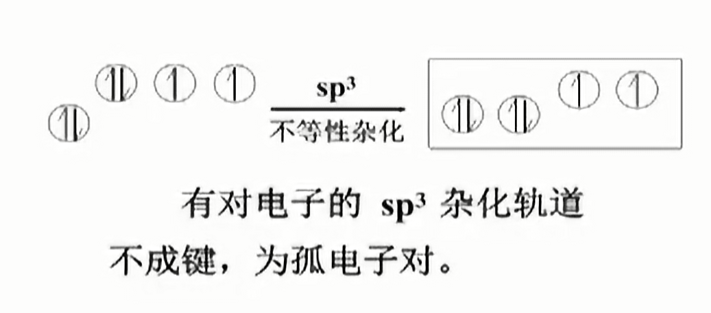
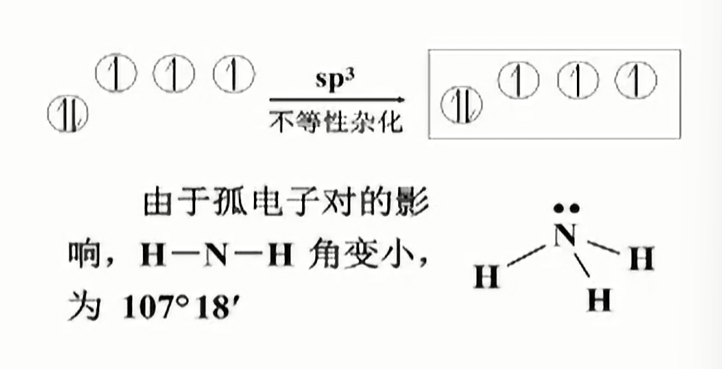
不等性杂化
主要是由于孤电子对的排斥力作用.
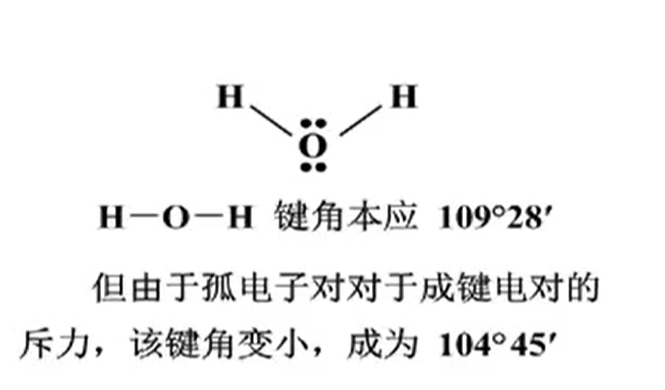
- Water molecules
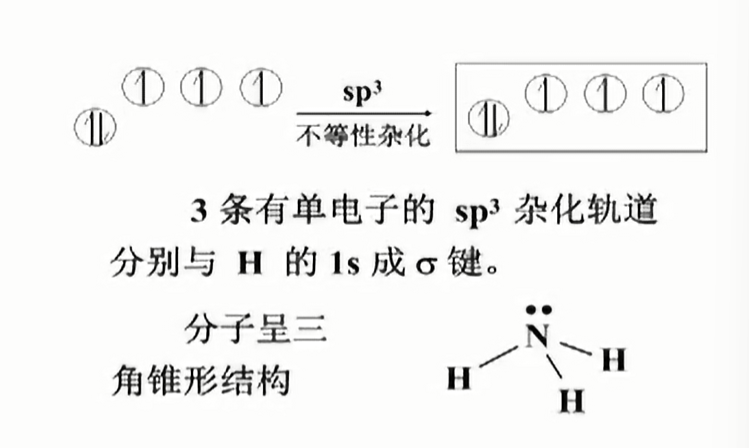
- ammonia
分子轨道理论 Molecular orbital theory
分子轨道的形成

现代共价键理论包括现代价键理论和分子轨道理论.
分子轨道——原子轨道的线性组合
现代价键理论中,电子在原子轨道中运动,属于特定的原子;而在分子轨道理论中,电子在分子轨道中运动,电子属于分子,而分子轨道由原子轨道线性组合得到.
分子轨道的数目与参与组合的原子轨道数目相等.
$H_2$中的两个$H$,共有两个$\psi_{1s}$,可组合成两个分子轨道:
$$
\begin{aligned}
&\psi_{MO}=c_1\psi_1+c_2\psi_2\\
&\psi_{MO}^{*}=c_1\psi_1-c_2\psi_2
\end{aligned}
$$
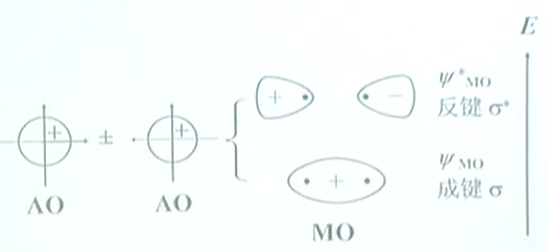
成键分子轨道比原先的轨道能量低,反键分子轨道比原先的轨道能量高.
两个$s$轨道($\psi_{AO}$)只能“头碰头”组合成$\sigma$分子轨道$\psi_{MO}$和$\psi_{MO}^{*}$.
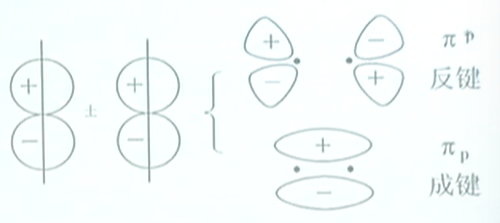
对于两个$p$轨道,当$p_x$与$p_x$“头碰头”地组合成$\sigma_{p_x}$和$\sigma_{p_x}^{*}$时,$p_y$与$p_y$,$p_z$与$p_z$“肩并肩地”组合成$\pi_{p_y}$和$\pi_{p_y}^{*}$,$\pi_{p_z}$和$\pi_{p_z}^{*}$分子轨道.
线性组合三原则
- 对称性一致原则
- 能量相近原则
- 最大重叠原理
其中,前两条为形成分子轨道的必要条件.
- 对称性一致原则
对核间连线呈相同对称性的轨道可以进行线性组合.
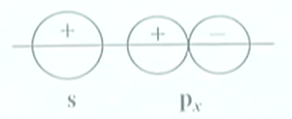
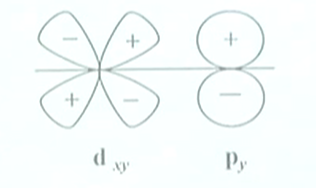
除$s-s,p-p$外,还有$s-p_x$沿$x$方向的组合,两者的对称性一致,组成$\sigma$分子轨道.
$p_y-d_{xy}$沿$x$方向,也可以组合成有效的$\pi$分子轨道.
- 能量相近原则
根据$I_1$值估算(将第一电离能近似地看作是轨道能量)
- 最大重叠原理
在对称性一致,能量相近的基础上,原子轨道重叠越大,越易形成分子轨道,即共价键越强.
分子轨道电子排布与分子轨道图 MO diagrams
分子轨道的能量与组成它的原子轨道能量相关,能量由低到高组成分子轨道能级图.
绘图基本步骤:
- 画出原子轨道(电子亚层)
- 按照Hund’s rules,分别在两侧的AO轨道上填充价电子
- 用两侧的价电子,共同填充中间的MO轨道
分子轨道图$\iff$分子轨道式
键级 bond order
$$键级=\frac{成键电子数-反键电子数}{2}$$
由于电子总是先从能量较低的成键轨道开始排布,因此成键电子数总是多于反键电子数.
$He^{+}_2$的存在用价键理论不好解释,因为不存在两个单电子成对的问题;而用分子轨道理论,则认为有半键.
分子的磁学性质
电子自旋产生磁场,分子中有单电子时,各电子平行自旋,磁场加强,物质呈顺磁性;顺磁性物质在外磁场中显磁性,在磁天平中加重.
若分子中无单电子时,电子自旋场抵消,物质显抗磁性,或称反磁性、逆磁性;抗磁性物质在外磁场作用下出现诱导磁矩,与外磁场相排斥,故磁性物质在磁天平中略减重.
Refrence
【吉林大学-无机化学(国家级精品课)】 https://www.bilibili.com/video/BV1YJ411P7gC/?p=31&share_source=copy_web&vd_source=868da4379e8534f9c1816f0da4155bed
【Drawing Molecular Orbital Diagrams】
0 条评论