译 | 计算材料学导论 2.1 扩散的随机游走模型

在介绍更复杂的方法之前，我们先从一个基本过程的理论模型开始——扩散过程的随机游走模型。随机游走模型是材料研究中最简单的计算模型之一，因此可以帮助我们介绍计算机模拟背后的许多基本思想。此外，尽管随机游走模型十分简洁，但它是描述材料中最重要的过程之一——原子在固体中的扩散——的重要基础。

2.1 扩散过程的随机游走模型

扩散是原子在与系统中其他原子相互作用的影响下，从一个位置移动到另一个位置的过程。原子在一个位置停留的时间通常要比原子的振动周期更长，而原子转移到另一个位置所用的时间则极短，我们称之为“跳跃”（$jump$）。

我们现在所掌握的细节，还不足以恰当地描述这一过程（我们将在今后的章节中继续探究）。因此，我们将采用一个非常简单的模型，它忽略所有原子级别的细节，只关注跳跃。

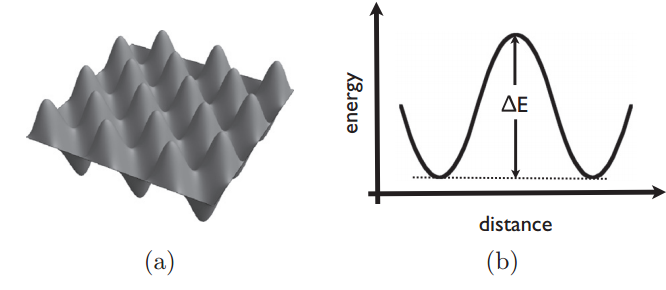
举个例子，一个原子沿着由正方形晶格组成的表面运动，相邻晶格点的距离为$a$。扩散过程是由原子在晶格点之间的一系列随机跳跃而产生的，如图2.1所示。通过考虑扩散原子与固体表面之间的能量传递，我们可以建立基本的物理过程，如图2.2a所示。原子将围绕其中一个势阱的底部震动，直到在一个方向上有足够的能量使其跳跃到相邻的位点。如图2.2b所示为位点间最低能量路径的能量面。

我们不能预测原子什么时候进行跳跃，也不能预测它将要跳跃到什么位置——这是一个随机（$stochastic$）过程。由动力学可知，我们知道原子跳跃的速率$k_{jump}$（单位为跳跃次数/时间）遵循Arrhenius型关系，取决于势垒的高度，这一过程通常被称为激活过程（$activated\ process$）。回顾图2.2a，我们可以看到相邻位点之间的能垒要比一个原子与其邻近位点之间的能垒高得多。因此，原子跳跃到下一个相邻位点的速率相对于仅仅跳跃到相邻位点是极低的，因而可以忽略不计。

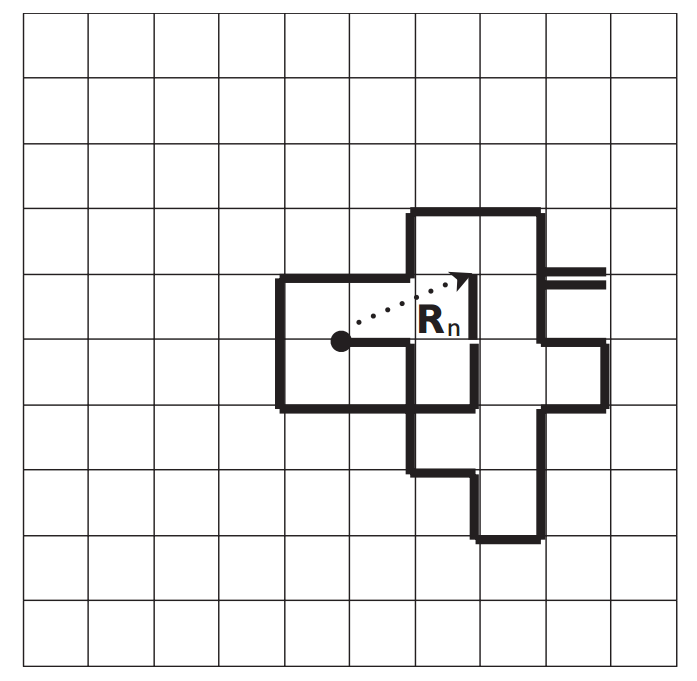
假设原子以方形晶格中的一个点为起点，将该点记作(0,0)。原子可以随机向相邻的四个位格任意跳跃，$r$，这四个位格分别记作$(0,1)a$（上），$(0,-1)a$（下），$(1,0)a$（右），$(-1,0)a$（左）。从原点开始，原子随机地向左、向右、向上或向下跳跃，这一过程重复$n$次。如果我们描绘这一系列跳跃的路径，看起来就像图2.1所示的那样。这种在空间中穿越的路径被称为“轨迹”（$trajectory$）。从某一点开始，原子将沿着它经过的轨迹反向运动——轨迹在平面上没有任何限制。由于所有的跳跃都是随机的，因此一系列跳跃被称为随机游走。若将原子放到原点重新进行以上过程，那么所得轨迹可能与图2.1完全不同，因为每次跳跃的方向都是完全随机的。

原子在晶格上的随机跳跃，是简单扩散模型的基础，因为建立模型仅需晶格参数（以及晶格长度）和跳跃速率$k_{jump}$即可，我们假设这些参数是已知的。

这些参量是模型的$input$（见1.4节）。不过为了得到$output$，还需要做一些工作。

我们的目标是计算原子在扩散中的运动，因此我们需要追踪它的位置。由于跳跃是随机事件，因此我们假设每次跳跃时间是不相关的（我们将在下文中重新讨论这个假设），我们可以将每次跳跃视为具有平均跳跃速率$k_{jump}$的随机事件，即平均跳跃速率除以时间。

由于跳跃的起点是任意的，我们假设原子在时间$t=0$时刻位于$(0,0)$，这是最简单的设定。一次跳跃后的位置由$r_1$给出，它将是原子随机选择的四个相邻位点中的一个。第二次跳跃后则是距离第一次跳跃后所处位置最近的位点。同样，我们仍不知道原子将往哪个方向移动。我们可以重复这个过程来创建一个跳跃序列。第$n$次跳跃后的位置，记作$R_n$，即为序列中每次跳跃的向量和。

$$
R_n = r_1 + r_2 + \cdots + r_n = \sum_{k=1}^{n} r_k,\ \ \ \ (2.1)
$$

即$r$的四种可能性在$n$次跳跃中随机选择的集合。

我们现在掌握了扩散过程随机游走模型的理论基础。用这种方法，我们可以追踪一个原子在某物质表面上的扩散。我们看到的扩散是一个随机过程，每个跳跃序列沿表面创建了一条路径。然而，我们还需要找到一种方法来检验该模型是否对扩散过程进行了合理的描述。为了做到这一点，我们需要将模型与便于测量的参量建立联系。对于扩散过程，最显著的参量是扩散系数（$diffusion \ coefficient$）。