1 二重积分
二重积分的核心就是旋转;极坐标是旋转的坐标系,而积分上下限的探究都是从旋转的视角来判断的.
1.1 基本计算方法
控制变量,分方向看问题.
偏导数的求解思想是分别固定两个变量为常数,求两次导数;而二重积分的思想也是与之一致的,可以称之为“偏积分”

先固定$x$为常数,即有对$y$的定积分$\int_{\varphi_1(x)}^{\varphi_2(x)}f(x,y)dy$,再对$x$求积分,即有$M=\int_{a}^b(\int_{\varphi_1(x)}^{\varphi_2(x)}f(x,y)dy)dx$.
将以上过程用更加简洁的符号来表示,记作:
$\iint_Df(x,y)d\sigma=\int_a^bdx\int_a^b\int_{\varphi_1(x)}^{\varphi_2(x)}f(x,y)dy$
tips:下限$\leq$上限
1.2 二重积分的运算性质
- 线性性
- 区域可加性
- 均匀面密度
$\ $线性性
积分区域$D$不动,拆被积函数$f(x,y)$.
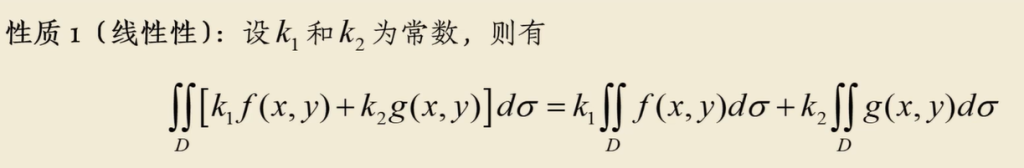
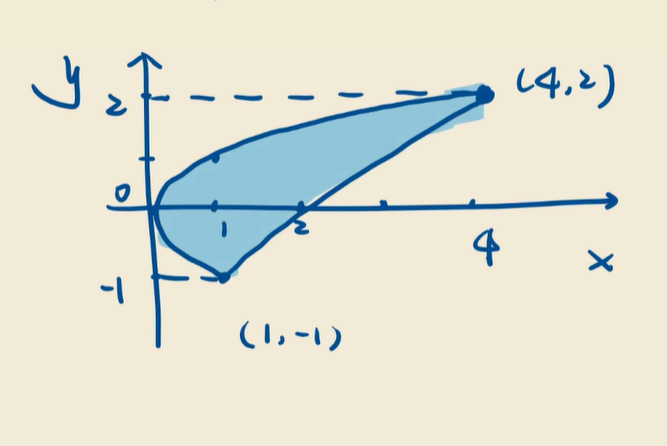
$\ $区域可加性
被积函数$f(x,y)$不动,拆积分区域$D$.

例题:

$\ $均匀面密度
从质量的角度考虑,该情形如下:铁皮的面密度是均匀的(恒为1)
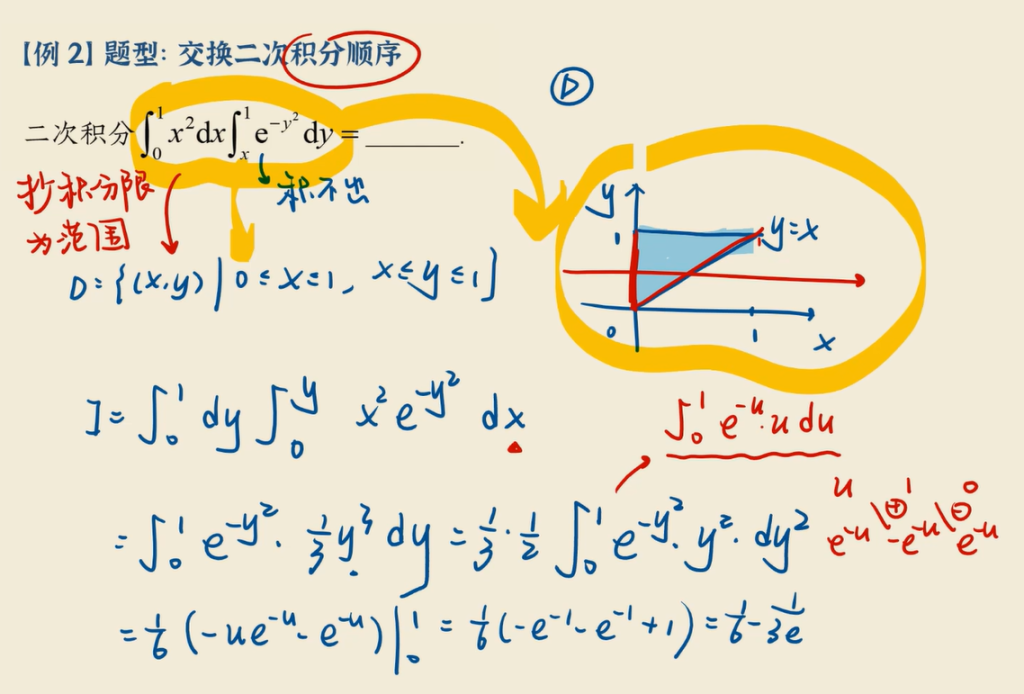
1.3 交换二次积分顺序
二重积分的被积函数和上下限函数有什么关系?
对于内部积分,如果难以计算,就需要交换内外的定积分顺序.
1.4 二重积分的画图
【二重积分不会画图怎么办?解决了这个疑惑再上考场!【近五年频繁考察,今年可能还会考】】
1.5 极坐标换元
换元后,原式中有两个元素会发生变化:
- 被积函数$f(x,y)$
- 被积区域$D$
- 积分上下限
可以将直角坐标系化为极坐标的情况
- 有重要暗示的时候
- 被积函数:出现$\sqrt{x^2+y^2},x^2+y^2,\frac{y}{x},\frac{x}{y}$等的时候,可以尝试极坐标换元法
- 积分区域:出现$x^2+y^2=R^2$,或$(x+a)^2+y^2=R^2$
积分区域为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,可以尝试令$x=arcos\theta,y=br\sin\theta$,
由于雅可比行列式,此时$dxdy=abrdrd\theta$
极坐标转换直角坐标系的基本方法
$$
\begin{cases}
x=r\cos\theta\\
y=r\sin\theta
\end{cases}
$$
$$ \iint_D f(x,y)dxdy =\int_{\alpha}^{\beta}d\theta \int_{r_1(\theta)}^{r_2(\theta)}f(r\cos\theta,r\sin\theta)rdr $$
基本步骤:
- 判断是否需要替换为极坐标形式
- 用$rd\theta dr$替换$dxdy$
- 寻找积分$dr,d\theta$的上下限
- 列出二重积分表达式
确定$\theta$的上下限,就是画两道射线将被积区域包裹起来,分别取这两道射线和$x$轴的夹角
确定$r$的上下限,就是取两道曲线,这两道曲线组成被积的封闭区域(上限一定大于下限)
【极坐标形式下的r和θ如何确定?【考研数学】】 https://www.bilibili.com/video/BV1VU4y1t73Q/?share_source=copy_web&vd_source=868da4379e8534f9c1816f0da4155bed
【【高数二重积分篇】极坐标系的积分区域(上)】
【【高数二重积分篇】直角坐标转极坐标(下)】
极坐标转化直角坐标
【极坐标如何转化成直角坐标?(张宇基础30讲1.12.1)】https://www.bilibili.com/video/BV1ip4y117SZ/?spm_id_from=333.337.search-card.all.click&vd_source=871fe5071dc7f3c7d940f39b5d33b2d8
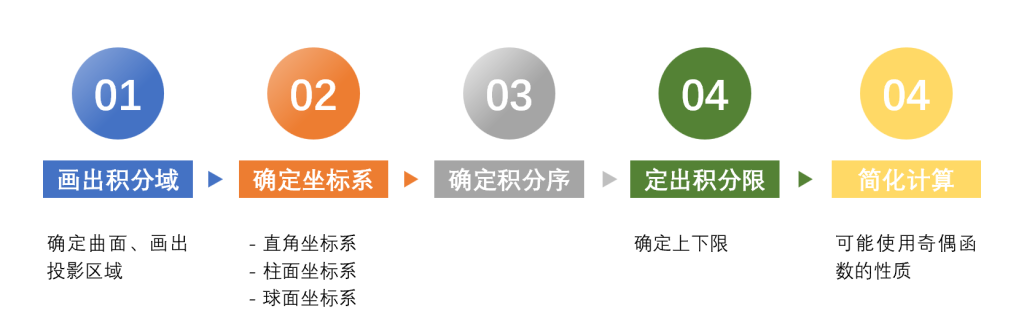
2 重积分的实际应用
2.1 概述
能用重积分解决的实际问题的特点
对于所求量,有以下两点要求:
- 分布在有界闭域上的整体量
- 对区域具有可加性
重积分解决问题的方法
- 微元分析法(元素法)
- 从定积分的定义出发,建立积分式
解题流程
2.2 物体的转动惯量
因质点系的转动惯量等于各质点转动惯量之和,故连续体的转动惯量可用积分计算.
以下是质点系和连续薄片的转动惯量:

连续物体的转动惯量:

半圆薄片
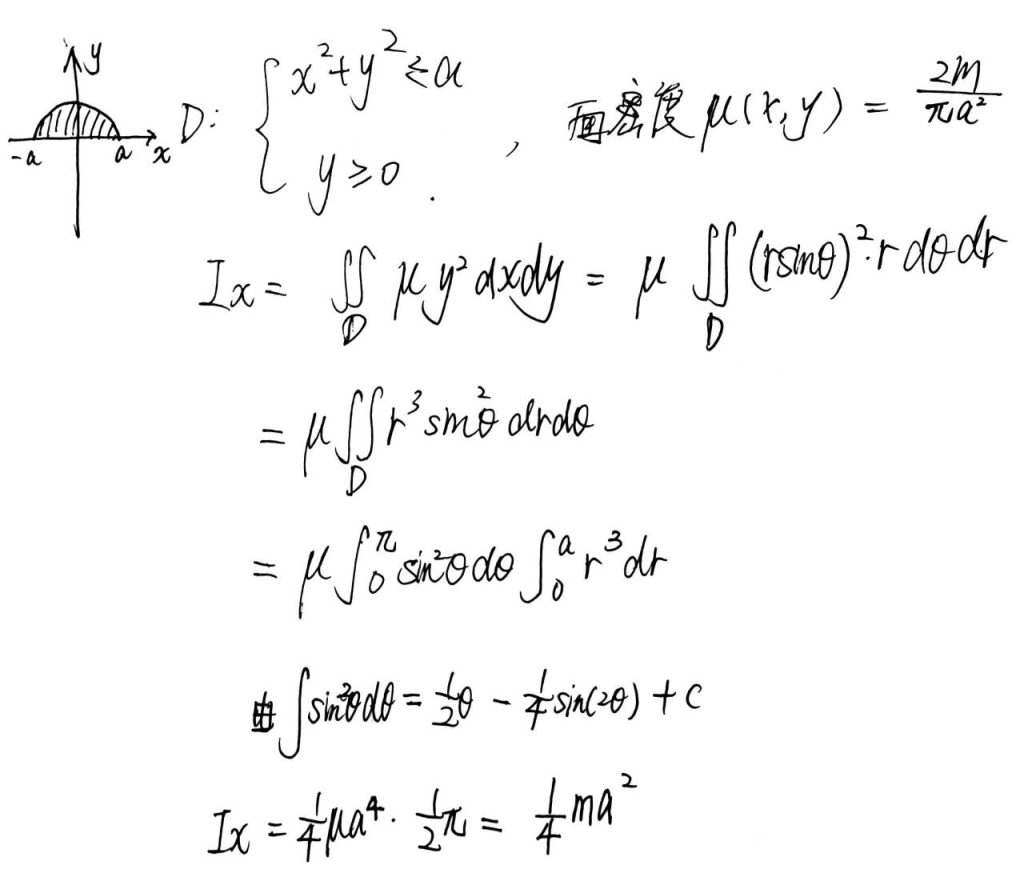
Refrence
0 条评论