基于罗尔定理构造辅助函数
- 原函数法
- 万能构造
- 常数$K$值
- 两次构造
- 函数转换
原函数法
运用罗尔定理的逆过程,寻找原函数.
运用罗尔定理的过程
$F(a)=F(b) \Rightarrow \exists \xi, F'(\xi)=0\Rightarrow s(\xi)-t(\xi)\Rightarrow s(\xi)=t(\xi)$
逆向过程
$s(x)=t(x) \Rightarrow s(x)-t(x)=0 \Rightarrow \int [s(x)-t(x)]dx=C \Rightarrow F(x)=C$
其中$F(x)$即为辅助函数.
罗尔定理的导函数可以被拆分为两个函数,而$F'(\xi)=0$则给了这两个函数相等的条件,从而可以运用其逆过程证明两个函数相等.
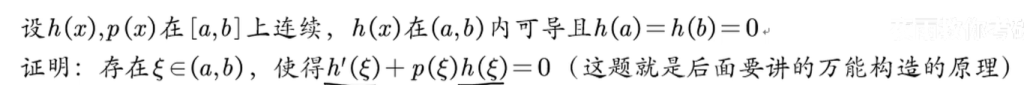
$p(\xi)$是无所谓的,可以进行任意操作,因为很显然它并不影响这个结论.
例题

回顾一下这个流程:先把欲证结论整理为$F(x)=C$的形式,如此一来就有$F'(x)=0$,这其实就是我们要得到的有力工具.
例题

拉格朗日与柯西中值定理
拉格朗日中值定理的几何定理
泰勒中值定理
Refrence
0 条评论