0 机械臂运动学概述
正运动学 Forward Kinematic
- Input:关节角
- Output:末端执行器位姿
逆运动学 Inverse Kinematic
- Input:关节角
- Output:各关节变量
DH参数共有四个($\alpha_i, a_i, d_i, \theta_i$),用以表达关节之间位置角度关系:两个用于描述自身,两个用于描述和相邻坐标系之间的几何关系.
问:为什么六自由度机械臂,仅通过四个DH参数就可以描述?
答:DH法通过限制原点位置与X轴的方向,人为地减少了两个自由度,因此只需四个DH参数,即可表达六自由度机械臂坐标变换.
问:是否有DH无法表达的坐标变换?
答:有;当 i-1 坐标系的X轴与 i 坐标系的Z轴平行时,DH坐标系无法表达这两个坐标系之间的坐标变换.
1 齐次坐标与变换矩阵
1.1 齐次坐标与缩放不变性(Scale Invariant)
通过$n+1$维来代表$n$维坐标,则该$n+1$维坐标即为$n$维坐标的齐次坐标;引入齐次坐标,主要是合并矩阵运算中的乘法和加法,将这两种变换放在同一个$4\times 4$矩阵中表示.
齐次变换坐标的规范化形式为:
$$ p=[x_0\ y_0\ z_0\ 1]^{\text T} $$
1.2 旋转矩阵
验证旋转矩阵的正确性,可以通过设置旋转角为0,然后观察矩阵是否是一个单位阵.
1.3 固定坐标系与相对坐标系
- 固定坐标系:左乘(从右向左连乘矩阵)
- 绝对坐标系:右乘(从左向右连乘矩阵)
2 正运动学 Fk
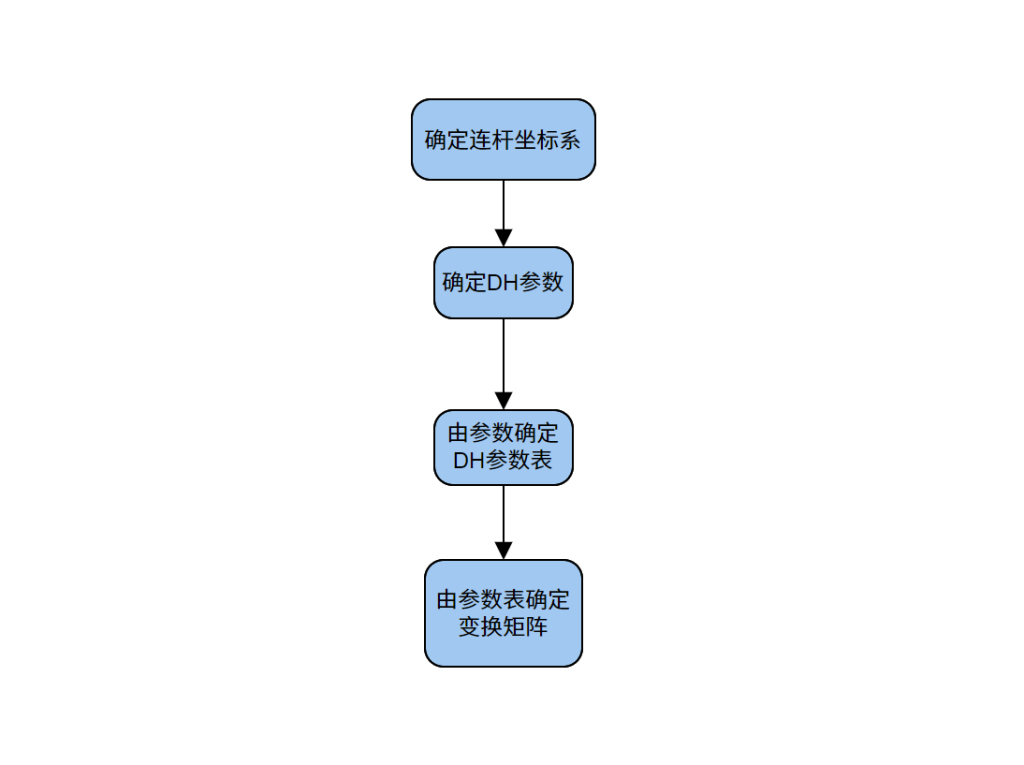
2.1 确定坐标系与DH参数
右手坐标系:以逆时针旋转为正,以顺时针旋转为负.
2.1.1 DH参数
- $\theta_i$:绕$z_i$轴,由$x_{i-1}$轴转向$x_i$轴的关节角度大小
- $d_i$:沿$z_i$轴,从$x_{i-1}$轴移动到$x_i$轴的距离
- $\alpha_{i-1}$:绕$x_i$轴,由$z_{i-1}$轴转向$z_i$轴的关节角度大小
- $a_{i-1}$:沿$x_{i-1}$轴,从$z_{i-1}$轴移动到$z_i$轴的距离
2.1.2 DH建系的四项规则
- z轴是旋转关节的旋转轴
- x轴必须垂直于当前z轴
- x轴必须与前一个z轴垂直
- y轴由x轴和z轴通过使用右手坐标系确定
2.1.3 详细步骤
- z轴
- 旋转关节:垂直于关节的旋转平面,以右手定则大拇指指向为正方向
- 伸缩关节:沿关节的伸缩直线运动的方向为正方向
- x轴
- 两Z轴不平行不相交:沿两Z轴的公垂线方向为X轴正方向
- 两Z轴平行:按任一公垂线为X轴(两坐标系平行)
- 两Z轴相交:按两轴的叉积方向为X轴
3 逆运动学 Ik
在 D-H参数及机器人的期望位姿已知的情况下,求解机器人满足该期望位姿的各个关节变量.
逆运动学并非只有单一求解方法,可以通过纯代数方法求解析解,也可以用算法求数值解
本质上,我们天然地已知一个角度,那就是末端执行器初始方向和原点与目标点连线之间的夹角,这是固定的已知关节角.
Refrence
斯沃仿真软件
http://www.swansc.com/cn/download/index.html
标准DH法建系过程
https://www.bilibili.com/read/cv17383646/
3D机械臂模型下载
https://www.traceparts.cn/zh
IRB1410规格
https://www.imrobotic.com/news/detail/23187
ABB IRB1410重力矩MATLAB计算
https://ww2.mathworks.cn/matlabcentral/answers/2128411-calculating-gravity-torque-for-abb-irb1410
IRB1410运动学分析与仿真
https://m.fx361.com/news/2022/1130/16850136.html
基于MATLAB的ABB机器人运动学分析与仿真
https://ieeexplore.ieee.org/document/9050992
带连杆的ABB机器人运动学计算
https://www.imrobotic.com/news/detail/23187
ABB六轴机械臂DH建系实例
https://blog.csdn.net/weixin_43236944/article/details/122218827
Matlab 六自由度机器人运动学逆解
0 条评论